Competitive Exams

IIT JEE, NEET, ESE, GATE, AE/JE, Olympiad

Only IAS

UPSC, State PSC

School Preparation

Foundation (Class 6-12), Commerce, Arts, CuriousJr (1st - 8th), Science, International Boards

Govt Exam

Judiciary, SSC, Defence, Teaching, JAIIB & CAIIB, BIHAR EXAMS WALLAH, UP Exams, Railway, Nursing Exams, Banking, WB Exams

UG & PG Entrance Exams

MBA, IPMAT, IIT JAM, LAW, CUET UG, UGC NET, GMAT, Design & Architecture, Pharma, CSIR NET, CUET PG, NEET PG

FINANCE

CA, CS, Finance Courses, ACCA

Others

English Wallah, Online Degrees

English Proficiency Test

IELTS, TOEFL

Agriculture

Area of a Sector Definition, Formula, Derivation, and Examples

Area of a Sector is defined as the portion of a circle enclosed by two radii and an arc. Learn the steps to calculate the area of a sector with examples here.

Chandni 17 Jan, 2025

The Area of a Sector is the area of the pie-shaped portion of any circular shape we often encounter in day-to-day life. The concept of the sector and the calculation of its area have significant applications in mathematics, science, and engineering.

In this article, we will let you know about the sectors of a circle and the different ways to determine their area to help you understand and apply the concept comprehensively. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]

What is a Sector?

The sector of a circle is the portion of a circle formed by a part of the circumference (also known as an arc) and the two radii of the circle that touch the circle circumference at the two ends of the arc. So, it is an area enclosed by an arc and two radii originating from the circle's center. The angle between the two radii determines the size of the sector.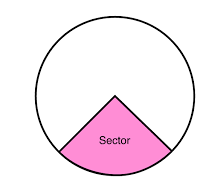 sector

Minor and Major Sectors

The two radii in the circle always form two sectors, one smaller and the other larger. These are explained below. Minor Sector: It is the smaller sector formed by the two radii when the angle between them is less than 180 degrees. Major Sector: It is the larger sector formed by the two radii where the angle between them is more than 180 degrees.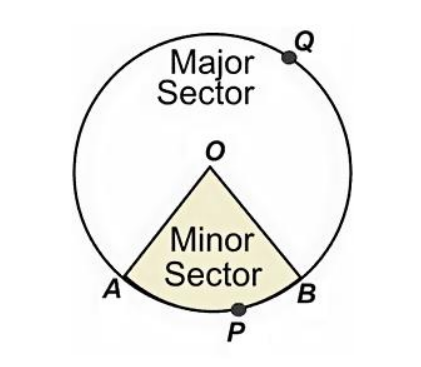

sectors

In the above figure, two radii OA and OB from the center O touch the circle circumference at points A and B, forming two different sectors. The sector OAB is smaller and is called the minor sector. The OAQB sector is larger and is called the major sector. The angle AOB formed at the center determines the size of the sectors.

Area of Sector of a Circle

The area of a sector is the space occupied by that particular portion or'slice' of the circle within the total boundary of the circle. It is observed that the area of a sector depends on the angle created by the two radii at the center of the circle. The size of the area increases with the increase in this angle. It means the area of a sector is directly proportional to the angle formed at the center of the circle. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]

Area of a Sector Formula

The formula for sector area is based on the ratio of the angle formed at the center to the total angle. There can be two formulas for the sector of a circle, as mentioned below.

When the Angle is in Degrees

When θ is the angle at the center given in degrees and r is the radius of the circle, then the Area of sector = (θ/360) × πr ²

When the Angle is in Radians

When θ is the angle at the center given in radians and r is the radius of the circle, then the Area of the sector = (θ/2π) × πr ² = ½θ x r ²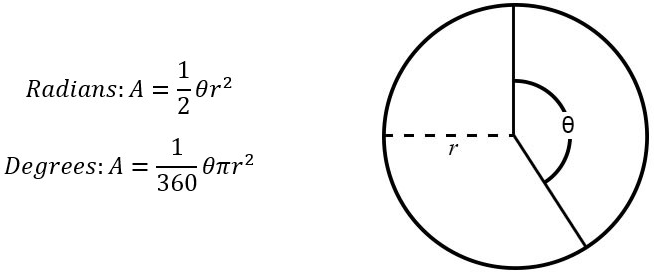

Area of Sector Formula Derivation

The area of the sector of a circle is derived using the following two concepts:

The area of a circle is πr ² where r is the circle's radius.
The angle at the circle's center, which encompasses the entire area, is 360 degrees.

Therefore, the area of a circle is πr ² , which corresponds to the angle of 360 degrees. U sing the unitary method, we can say that if the two radii form an angle of 1 degree at the center of the circle, then the area of a sector formed will be πr ² /360. Similarly, if the angle formed at the center of the circle is θ, the Area of the sector formed will be (θ/360) × πr ²

Steps to Find Area of Sector Using Arc Length

The area of the sector of a circle can be determined without knowing the angle formed at the center. In that case, we require the length of the arc corresponding to that sector for calculation purposes. If the length of the arc is given as l and the radius of the circle is r, we can derive the formula for the sector as follows: According to the radian definition, the angle at the center of the circle corresponding to a sector is the ratio of arc length to the radius of the circle. So in this case, if θ is the angle in radians, then θ = l/r So, the area of sector A = ½θ x r 2 = ½ (l/r) x r 2 = (l x r) /2

Area of Sector Solved Examples

1. Find the area of a sector with a 7 cm radius and a central angle of 60°.

Solution:

r = 7 cm, θ = 60° Using the formula of area of sector = θ/360× π r 2 , we get, Area = 60/360 x 22/7 x (7) 2 = 1/6 x 22 x 7 = 25.67 square cm.

2. Find the area of a sector with a 4 cm radius and a central angle of π/4 radians.

Solution:

r = 3 cm, θ = π/4 So, the area of the sector = ½ x (4) 2 x π/4 = (16/2) x π/4 = 2π = 6.28 square cm.

3. Find the areas of minor and major sectors formed by an angle of 120 degrees in a circle of radius 5 cm.

Solution:

The angle made by the sector is θ = 120°. It is a minor sector So, the area of the minor sector = (120°/360°) × (22/7) × 5 2 = 1/3 × 22/7 × 25 = 26.17 square cm. The angle for the major sector is 360°- 120° = 240° So, the area of the major sector = (240°/360°) × (22/7) × 5 2 = 2/3 × 22/7 × 25 = 52.34 square cm.

4. The arc length of a sector is 10 cm, and the radius of the circle is 6 cm. Find the area of the sector.

Solution:

The arc length l = 10 and radius r = 6 Using the formula for the area of sector A = (l x r) /2, we get, Area of sector = (10 x 6)/2 = 30 square cm. The sector of a circle is an interesting mathematical concept that has various practical applications. An understanding of the area of a sector for any circular shape gives a clear idea of how much portion of the total circle you are taking into consideration and how it is related to the angle created at the center of the circle.

Related Articles
Corresponding Angles	Isosceles Triangle
Average Speed Formula	Differentiation
Ratio	Surface Area of Cylinder

Area of Sector FAQs

When do the areas of minor and major sectors become equal?

Ans. The areas of the minor and major sectors become equal when the angle formed at the center of the circle by two radii is 180 degrees.

What is a very common practical example of a sector of a circle?

A very common practical example of the sector of a circle is the slice of a pizza.

Can a circle have more than one sector?

A circle can have more than one sector formed by different radii.

How many sectors can be formed with an angle of 30 degrees formed by the radii at the center of a circle?

There will be 12 equally-sized sectors formed by different radii with an angle of 30 degrees between two consecutive radii.

If a circle has 8 sectors of equal area, what will be the central angle for each of them?

The central angle for each of these equal 8 sectors will be 45 degrees since all of them add up to 360 degrees.

🔥 Trending Blogs

What are Extracurricular Activities, Types and Benefits

NCERT Solutions for Class 5 Maths Chapter 9 Boxes and Sketches

Mental Maths Questions With Solutions, Download PDF

Natural Phenomena for Class 8 Junior Explorers

Addition Word Problems for Class 3, Download PDF

Talk to a counsellorHave doubts? Our support team will be happy to assist you!

7019243492

07019243492

Check out these Related Articles

CURIOUS JUNIOR

Even Numbers: Definition, Example, Properties, List 1 to 1000

Read Full Story

1 Aug 2025, 01:13 pm

CURIOUS JUNIOR

Separation of Substances: Class 6 Science

Read Full Story

1 Aug 2025, 01:09 pm

CURIOUS JUNIOR

Trapezium: Properties, Types, Formulas, and Applications

Read Full Story

1 Aug 2025, 01:12 pm

CURIOUS JUNIOR

Adjectives - Definition, Types, Forms, Usage, Examples

Read Full Story

1 Aug 2025, 01:08 pm

CURIOUS JUNIOR

List of Homophones Words A to Z

Read Full Story

1 Aug 2025, 01:07 pm

CURIOUS JUNIOR

How to Write 15000 in Words in English, Check Here

Read Full Story

1 Aug 2025, 01:06 pm

CURIOUS JUNIOR

Class 8 Sound: Adventure into the World of Sound

Read Full Story

1 Aug 2025, 01:05 pm

CURIOUS JUNIOR

What are Length, Width, and Height: Key Differences with Examples

Read Full Story

1 Aug 2025, 01:04 pm

CURIOUS JUNIOR

Odd Numbers: Definition, Types, Examples and Properties

Read Full Story

1 Aug 2025, 01:03 pm

Join 15 Million students on the app today!

Live & recorded classes available at ease

Dashboard for progress tracking

Millions of practice questions at your fingertips

Free Learning Resources

PW Books

Notes (Class 10-12)

Class 10 Math's Notes

Class 10 Chemistry Notes

Class 10 Physics Notes

lass 10 Biology Notes

Aptitude & Reasoning

Class 10 Geography

Physics Class 11 Notes

Class 11 Chemistry Notes

Maths Notes Class 11

Zoology Class 11

Class 11 Botany Notes

Physics Class 12 notes

Chemistry Class 12

Maths Notes Class 12

Zoology class 12

Class 12th Botany Notes

PW Study Materials

Arjuna JEE Study Material

JEE 5 PYQs

JEE Mind Maps

Yakeen Study Material

NCERT Punch

Arjuna Neet Study Material

NEET PYQs

CBSE Sample Paper

CBSE Question Bank

Udaan For Class 10th Study Material

Notes (Class 6-9)

Class-6 Theory & Notes

Math's Notes for class 7

Science Notes for class 7

Class 8 Math Notes

Class 8 Chemistry Notes

Class 8 Physics Notes

Class 8 Biology Notes

Class 8 SST Notes

Class 9 Math's Notes

Class 9 Physics Notes

Class 9 Chemistry Notes

Class 9 Biology Notes

Ncert Solutions

NCERT Solutions For Class 6

NCERT Solutions For class 7

NCERT Solutions for class 8

NCERT Solutions for class 9

NCERT Solutions for class 10

NCERT Solutions for class 11

NCERT Solutions for Class 12

NCERT Solutions For Class 6

Govt Exams

Entrance Exams

Our Other Websites

Class 6th to 12th Online Courses

Class 12 Online Course

Class 11 Online Course

Class 10 Online Course

Class 9 Online Course

Class 8 Online Course

Govt Job Exams Courses

SSC Online Coaching

Bank Exam Online Coaching

TET Online Coaching

JAIIB & CAIIB Online Coaching

Bihar Exam Online Coaching

UPSC Coaching

UPSC Online Coaching

UPSC Offline & Hybrid Coaching

State PSC Online Coaching

UPPSC Online Coaching

BPSC Online Coaching

Defence Exam Coaching

NDA Online Coaching

CDS Online Coaching

AFCAT Online Coaching

Agniveer Online Coaching

Gate Exam Coaching

Civil Engineering Courses

Mechanical Engineering Courses

Formulas

Other Exams

Company Secretary Exam

Know about Physics Wallah

Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.

We Stand Out because

We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.

Our Key Focus Areas

Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.

What Makes Us Different

Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others

What is a Sector?

Minor and Major Sectors

sectors

Area of Sector of a Circle

Area of a Sector Formula

The formula for sector area is based on the ratio of the angle formed at the center to the total angle. There can be two formulas for the sector of a circle, as mentioned below.

When the Angle is in Degrees

When θ is the angle at the center given in degrees and r is the radius of the circle, then the Area of sector = (θ/360) × πr ²

When the Angle is in Radians

When θ is the angle at the center given in radians and r is the radius of the circle, then the Area of the sector = (θ/2π) × πr ² = ½θ x r ²

Area of Sector Formula Derivation

The area of the sector of a circle is derived using the following two concepts:

The area of a circle is πr ² where r is the circle's radius.
The angle at the circle's center, which encompasses the entire area, is 360 degrees.

Steps to Find Area of Sector Using Arc Length

Area of Sector Solved Examples

1. Find the area of a sector with a 7 cm radius and a central angle of 60°.

Solution:

r = 7 cm, θ = 60° Using the formula of area of sector = θ/360× π r 2 , we get, Area = 60/360 x 22/7 x (7) 2 = 1/6 x 22 x 7 = 25.67 square cm.

2. Find the area of a sector with a 4 cm radius and a central angle of π/4 radians.

Solution:

r = 3 cm, θ = π/4 So, the area of the sector = ½ x (4) 2 x π/4 = (16/2) x π/4 = 2π = 6.28 square cm.

3. Find the areas of minor and major sectors formed by an angle of 120 degrees in a circle of radius 5 cm.

Solution:

4. The arc length of a sector is 10 cm, and the radius of the circle is 6 cm. Find the area of the sector.

Solution:

Related Articles
Corresponding Angles	Isosceles Triangle
Average Speed Formula	Differentiation
Ratio	Surface Area of Cylinder