
A Ratio is a mathematical expression used to compare two or more quantities. It shows how many times one number contains another and is written in the form of "a:b" or as a fraction "a/b."
Ratios help illustrate relationships between different values, making them useful for solving problems in various fields such as finance, engineering, and everyday situations. Ratios can represent proportions, rates, or comparisons between quantities. They can be simplified by dividing both terms by their greatest common divisor (GCD) to make the ratio more understandable. Whether comparing distances, prices, or even ingredients in a recipe, it provide a clear and concise way to express relationships between numbers, enabling easier interpretation and decision-making. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]What is a Ratio?
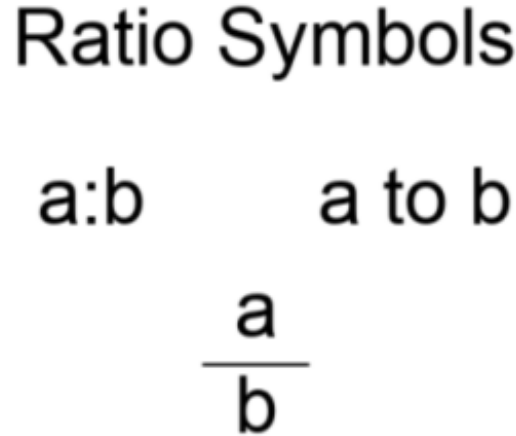 A ratio is a mathematical expression that compares two or more quantities, showing the relative size of one quantity to another. It is often represented in the form of a fraction, with the first quantity (the numerator) divided by the second quantity (the denominator).
Ratios can also be expressed using a colon (e.g., 3:2) or in words (e.g., "3 to 2").
Ratios are commonly used in various fields, including mathematics, finance, and statistics, to analyze relationships between different values. For example, in finance, a company's debt-to-equity ratio compares its total liabilities to its shareholders' equity, providing insight into its financial leverage.
In everyday life, ratios can help compare prices, proportions in recipes, or the relationship between different measurements. Overall, ratios are a useful tool for understanding and interpreting relationships between quantities.
A ratio is a mathematical expression that compares two or more quantities, showing the relative size of one quantity to another. It is often represented in the form of a fraction, with the first quantity (the numerator) divided by the second quantity (the denominator).
Ratios can also be expressed using a colon (e.g., 3:2) or in words (e.g., "3 to 2").
Ratios are commonly used in various fields, including mathematics, finance, and statistics, to analyze relationships between different values. For example, in finance, a company's debt-to-equity ratio compares its total liabilities to its shareholders' equity, providing insight into its financial leverage.
In everyday life, ratios can help compare prices, proportions in recipes, or the relationship between different measurements. Overall, ratios are a useful tool for understanding and interpreting relationships between quantities.
Also Check: Pythagoras Theorem
Ratio Formula
The formula for a ratio between two quantities, say 'a' and 'b', is expressed as: a : b or a/b This means that the ratio of 'a' to 'b' is the same as the fraction of 'a' over 'b'. To simplify the ratio, you divide both 'a' and 'b' by their greatest common divisor (GCD). For example, the ratio 6:9 can be simplified by dividing both numbers by 3, resulting in 2:3. In general:- Step 1 : Identify the two quantities (a and b).
- Step 2 : Divide both 'a' and 'b' by their greatest common divisor (GCD).
- Step 3 : Write the simplified ratio as a:b.
How to Solve Ratios?
Solving ratios can seem tricky at first, but with a clear process, you can tackle any ratio problem with confidence. Here’s a simple step-by-step guide to help you solve ratios effectively:Step 1: Understand the Ratio
- Identify the Ratio : Look at the ratio you are given. For example, if you have a ratio of 3:4, this means for every 3 parts of one quantity, there are 4 parts of another quantity.
- Know What You Are Comparing : Determine what the two quantities represent. For example, if the ratio is of boys to girls in a class, you need to know how many boys and girls there are.
Step 2: Set Up the Equation
- Use Variables : If you need to find the actual quantities, you can use variables. For example, if the ratio of boys to girls is 3:4, you can let the number of boys be 3x and the number of girls be 4x, where x is a common multiplier.
Step 3: Write the Ratio as a Fraction
- Convert to Fraction : You can express the ratio as a fraction. For the ratio 3:4, you can write it as 3/4 This can help you when you need to solve for unknowns.
Step 4: Cross-Multiply (if necessary)
-
Cross-Multiplication
: If you are solving a proportion (where two ratios are equal), you can use cross-multiplication. For example, if you have 4:3=12:x, you can cross-multiply:
- ( 3times 12 = 4times x )
- This gives you (36 = 4x).
Step 5: Solve for the Unknown
- Isolate the Variable : If you have an equation like ( 36 = 4x ), divide both sides by 4 to find x: (x = 36/{4} = 9).
-
Find the Quantities
: If you use variables in Step 2, substitute back to find the actual quantities. For example, if (x = 9), then:
- Number of boys = ( 3x = 3 \times 9 = 27 )
- Number of girls = ( 4x = 4 \times 9 = 36 )
Also Check: Area of Square
Types of Ratios in Maths
Ratios are an important concept in math that helps us compare different quantities. Understanding ratios can make it easier to solve problems in various subjects, from math to science and even finance. Here’s a simple guide to the different types of ratios you might encounter:- Simple Ratios : These are the most straightforward type of ratio, comparing two quantities directly. For example, if you have 4 apples and 2 oranges, the ratio of apples to oranges is 4:2, which can be simplified to 2:1. This means for every 2 apples, there is 1 orange.
- Compound Ratios : When you compare more than two quantities, you create a compound ratio. For instance, if a recipe calls for 2 cups of flour, 1 cup of sugar, and 3 eggs, the compound ratio is 2:1:3. This helps you understand the relationship between all the ingredients.
- Proportional Ratios : These ratios show that two ratios are equal. For example, if the ratio of boys to girls in one class is 3:4 and in another class is 6:8, these ratios are proportional because they simplify to the same value (3:4). This means the relationship between boys and girls is the same in both classes.
- Part-to-Whole Ratios : This type of ratio compares a part of a quantity to the whole. For example, if there are 20 students in a class and 8 of them are girls, the part-to-whole ratio of girls to the total number of students is 8:20, which simplifies to 2:5. This means that for every 5 students, 2 are girls.
- Rate Ratios : These compare two quantities with different units. For example, if a car travels 120 miles in 2 hours, the rate ratio is 120 miles/2 hours, which simplifies to 60 miles per hour. This tells you how fast the car is going.
Examples
Imagine a classroom where the teacher counts the number of boys and girls. The teacher finds that the ratio of boys to girls is 4:5. If there are 20 boys in the classroom, how many girls are there?Step 1: Understand the Ratio
The ratio of boys to girls is given as 4:5. This means that for every 4 boys, there are 5 girls.Step 2: Set Up the Ratio
Let’s denote:- The number of boys = ( 4x )
- The number of girls = ( 5x )
Step 3: Use the Known Quantity
We know that there are 20 boys. So, we can set up the equation: [ 4x = 20 ]Step 4: Solve for ( x )
To find ( x ), divide both sides of the equation by 4: [ x = \frac{20}{4} = 5 ]Step 5: Find the Number of Girls
Now that we have ( x ), we can find the number of girls: [ \text{Number of girls} = 5x = 5 \times 5 = 25 ]Step 6: Check the Ratio
Now, let’s check if the ratio of boys to girls is still 4:5:- Number of boys = 20
- Number of girls = 25
| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Differentiation |
| Perimeter of Rectangle | Surface Area of Cylinder |
Ratio FAQs
How do you simplify a ratio?
To simplify a ratio, divide both terms of the ratio by their greatest common divisor (GCD). This reduces the ratio to its simplest form.
Can ratios be written as fractions?
Yes, ratios can be written as fractions. For example, the ratio 3:4 can be expressed as 3/4.
How do you solve a ratio problem?
To solve a ratio problem, you can use cross-multiplication or division, depending on the type of problem. For example, to find an unknown quantity in a ratio, you can set up a proportion and solve for the missing value.
What are the types of ratios?
There are several types of ratios, including simple ratios (comparing two quantities), part-to-whole ratios, and rates (ratios comparing quantities with different units, such as miles per hour).
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App








