Cylinder: Shape, Formulas, Solved Examples
A cylinder is a three-dimensional geometric shape with two parallel, congruent circular bases connected by a curved surface. Explore the definition of a cylinder, its types, important formulas, and solved examples to understand its applications more effectively.
Chandni 8 Jan, 2025
Share
Cylinder: Take a moment to look around, and you will notice cylinders everywhere. From candles and soda cans to water tanks and pipes, this geometrical shape is all around us.
A cylinder is a three-dimensional object with two parallel circular bases connected by a smooth, curved surface. The word "cylinder" comes from the Greek word "kylindros," which means "roller" or "barrel." This name reflects the rolling nature of a cylinder, a characteristic that matches its shape in geometry. Since a cylinder is a three-dimensional geometric shape, it has two key properties: surface area, which measures its outer covering, and volume, which calculates the space it occupies.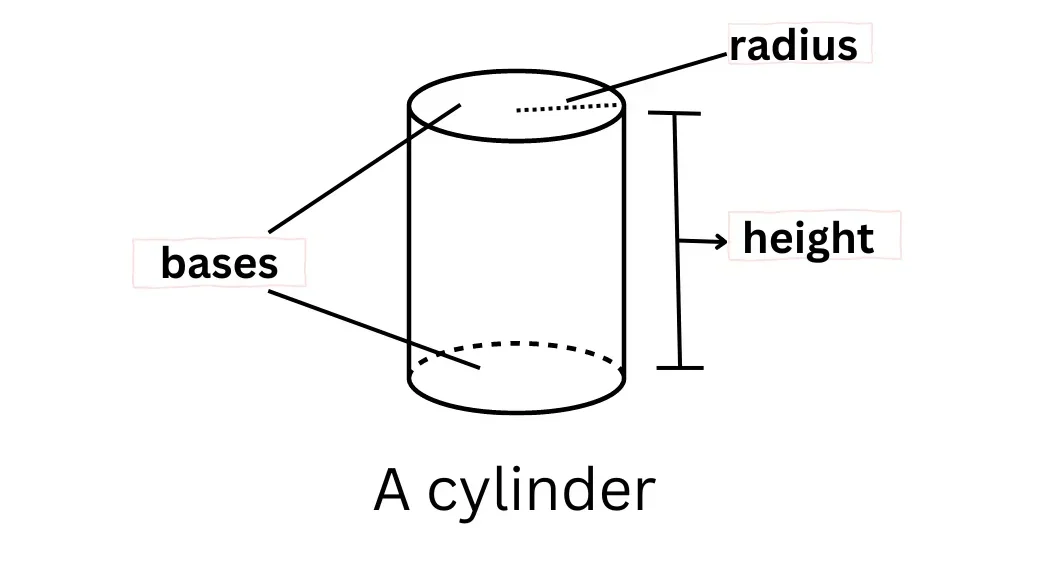
[video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]
Cylinder Definition
A cylinder is a three-dimensional shape defined by two identical, parallel circular bases connected by a curved surface. The line segment connecting the centers of the two circular bases is called the axis, representing the height of the cylinder. The distance from the center of a circular base to its edge is called the radius, denoted as “r.” This cylindrical shape is a blend of two circles and a rectangle.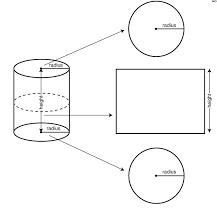
Cylinders are incredibly versatile and can be found in many objects around us. Examples include beverage cans, gas cylinders, drum barrels, batteries, telescope tubes, water bottles, and storage silos.
Number of Faces Vertices Edges in Cylinder
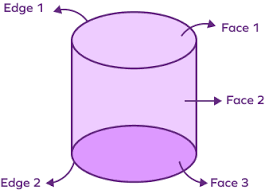
A cylinder is a geometrical shape with two flat circular faces and one curved surface. The two circular faces are identical in size and shape, positioned parallel to each other, one at the top and one at the bottom. These faces are connected by a curved surface, which looks like a rectangle rolled into a tube. If we think about its parts:- A cylinder has 3 faces.The two flat circular faces and the curved surface.
- It has 2 edges. One edge at the top where the curved surface meets the upper circle and one edge at the bottom where it meets the lower circle.
- It has 0 vertices because there are no sharp corners or points where edges meet.
Types of Cylinder
In geometry, cylinders are classified into four main types. These are as follows:Right Circular Cylinder
This type has two parallel circular bases, and the axis (the line joining the centers of the bases) is perpendicular to the center of the bases. The bases are directly aligned, making it a regular and symmetrical shape. A common example is a soda can, which stands upright with perfectly aligned circular ends.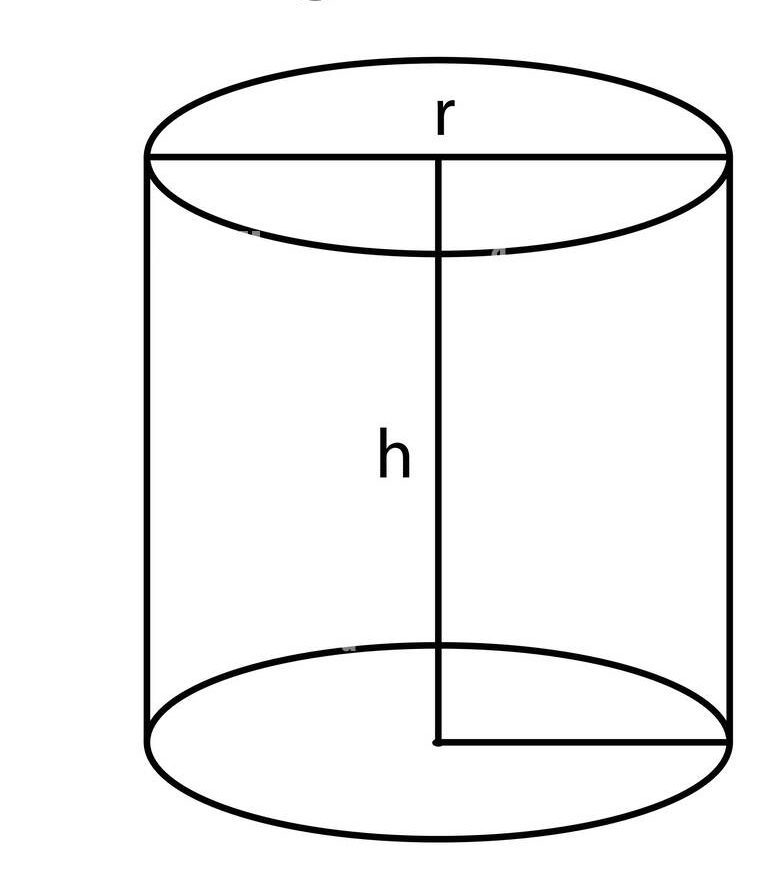
Oblique Cylinder
In an oblique cylinder, the sides are tilted, and the axis is not perpendicular to the bases. This means the top base is shifted sideways relative to the bottom base. The Leaning Tower of Pisa is a relatable example, as its tilted structure resembles the shape of an oblique cylinder.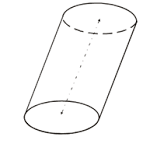
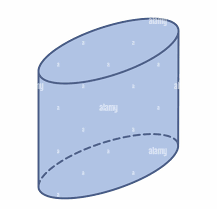
Elliptic Cylinder
Unlike the right circular cylinder, the bases of an elliptic cylinder are shaped like ellipses instead of circles. This gives the cylinder a unique elongated or flattened appearance. Optical lenses are a practical example of this type of cylinder, commonly used in scientific instruments.
Right Circular Hollow Cylinder (Cylindrical Shell)
This type consists of two right circular cylinders, one inside the other, creating a hollow space between them. The axis of both cylinders is common and perpendicular to the bases, but the structure is different because of the hollow interior. Hydraulic cylinders, which are used in heavy machinery, are a typical example of this design.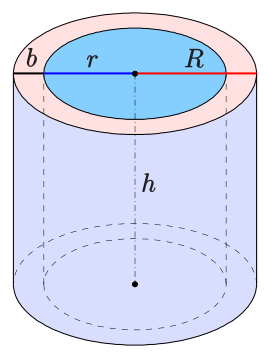
Cylinder Formulas
Cylinders have formulas to calculate their volume , curved surface area (CSA) , and total surface area (TSA) . These formulas are useful for understanding how much space the cylinder occupies and how much surface it has. Let’s understand each of the cylinder formulas briefly below.Volume of a Cylinder
The volume of a cylinder tells us how much space it occupies. Imagine a cylindrical container filled with oil; the volume will represent the total amount of oil it can hold. The volume of a cylinder is always measured in cubic units. V olume of a Cylinder Formula Volume (V) = πr 2 h (cubic units)- r : Radius of the circular base.
- h : Height of the cylinder (distance between the two bases).
- π : It is constant, approximately equal to 22/7 or 3.14
Curved Surface Area (CSA) of a Cylinder
The curved surface area (CSA), also called the lateral surface area, refers to the area of the cylinder's side, excluding the top and bottom bases. It’s like unrolling the curved part of a cylinder, similar to peeling off the label from a soda can or removing the outer layer of a roll of tape. T he curved surface area of a cylinder is always measured in square unitsCurved Surface Area of Formula
CSA = 2πrh (square units)- r : Radius of the circular base
- h : Height of the cylinder
Total Surface Area (TSA) of a Cylinder
The total surface area of a cylinder is the total area covering its outer surface. It includes three parts: the curved side surface and the two circular bases. Surface area is always measured in square units. Total Surface Area of a Cylinder Formula TSA = 2πr(h+r) (square units)- The term 2πrh is the curved surface area.
- The term 2πr 2 adds the areas of the two circular bases.
Cylinder Solved Examples
Example 1: Find the total surface area of a cylindrical drum with a radius of 5 feet and height of 10 feet in square feet.
Solution: Given: R = 5 feet, h = 10 feetFormula:
TSA=2πr(h+r)Substitute the values:
TSA=2π×5×(10+5) TSA=2π×5×15=150π square feet TSA≈150×3.14=471.00 square feetExample 2: Find the curved surface area of a pillar with a radius of 4 cm and height of 9 cm.
Solution: Given: r=4 cm, h=9 cmFormula:
CSA=2πrhSubstitute the values:
CSA=2 × 22/7 × 4 × 9 CSA=2 × 22 × 36 ÷ 7 CSA=2×22×36÷7 CSA≈226.29 square cm (rounded to two decimal places)Example 3: Find the radius of a cylinder with a curved surface area of 352 sq. cm and height of 8 cm.
Solution: Given: CSA=352 sq. cm, h=8 cmFormula:
CSA=2πrhSubstitute the values:
352 = 2 × 22/7 × r × 8 352 = 352/7 r r= 352/ (2×22×8÷7) =352 × 7/ 352 r=7 cmsExample 4: Find the total surface area of a cylinder if the curved surface area is 198 sq. cm, and the radius is 6 cm.
Solution: Given: CSA=198 sq. cm, r=6 cmThe formula for CSA:
CSA=2πrhFind height (h):
198 = 2×22/7×6×h 198 = 264/7h h = 198 × 7/ 264 = 5.25Now calculate TSA:
TSA=2πr(h+r) TSA=2×22/7×6×(5.25+6) TSA=2×22/7×6×11.25 TSA≈ 2 × 3.14 × 6 × 11.25 = 424.1 sq. cm (rounded to two decimal places)Example 5: Find the volume of a cylindrical water tank with a radius of 7 feet and a height of 12 feet.
Solution: Given: r=7 feet, h=12 feetFormula for volume:
Volume (V)=πr 2 hSubstitute the values:
V=22/7 ×7 2 ×12 V=22/7 × 49 × 12 V=22×49×12÷7 V = 22 × 84 = 1848 cubic feet The volume of the water tank is approximately 1847.52 cubic feet.| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Differentiation |
| Perimeter of Rectangle | Surface Area of Cylinder |
Cylinder FAQs
How is a cylinder different from a prism?
Both have parallel bases, but a cylinder has curved surfaces and circular bases, while a prism has flat surfaces and polygonal bases.
What happens to the surface area if the height of a cylinder is doubled?
When the height of a cylinder is doubled, the curved surface area increases proportionally, while the base areas remain unchanged. For example, a cylinder with a radius of 3 cm and a height of 5 cm has a curved surface area (CSA) of 2π(3)(5)=94.2 sq cm. . If the height is doubled to 10 cm, the CSA becomes 2π(3)(10)=188.4 sq cm. 2.. The CSA doubles, but the base areas stay the same.
How do engineers use cylinder formulas in real-life applications?
Engineers use TSA and CSA for material estimates and surface coatings, and volume for storage or capacity calculations in tanks and pipelines.
Can the CSA of a cylinder ever exceed its TSA?
No, because the TSA always includes the CSA plus the areas of the two bases.
Can a cylinder roll on its side?
Yes, a cylinder can roll on its side because of its smooth, curved surface, which allows it to move easily in a straight line when pushed or given momentum
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.