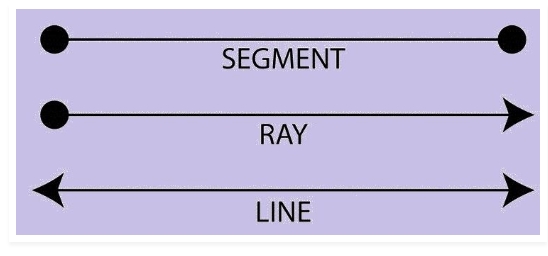
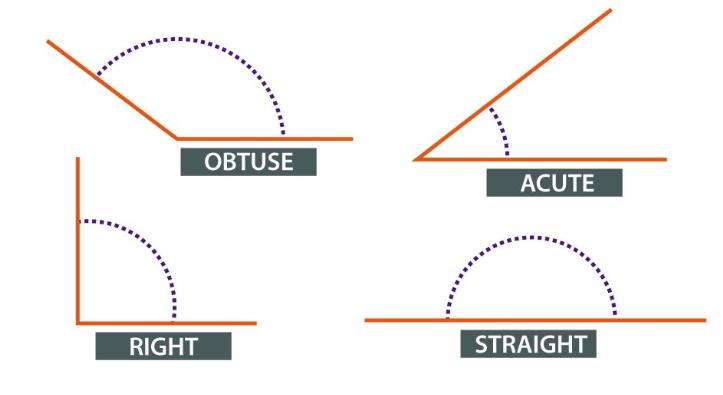
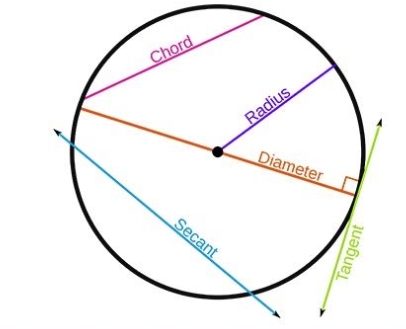
Geometry: Geometry for kids introduces the basics of shapes, sizes, and their properties in a fun and interactive way. It begins with understanding simple 2D shapes like circles, squares, triangles, and rectangles, progressing to 3D shapes like cubes, spheres, and pyramids.
Kids learn about angles, symmetry, and measuring lengths and areas. Visual aids, hands-on activities, and games help make abstract concepts more relatable. Geometry enhances spatial thinking, logical reasoning, and problem-solving skills, laying a foundation for more advanced mathematical concepts. By connecting geometry to the real world, it sparks curiosity and fosters an appreciation for math.Also Check: Pie Chart
About CuriousJr Mental Maths Classes
At CuriousJr , part of Physics Wallah, we provide specialized Mental Maths Classes that help students master problem-solving skills. With over 50 mental math strategies our program is designed to enhance both speed and accuracy in calculations. Our classes focus on developing logical reasoning and critical thinking skills enabling students to tackle complex problems effortlessly. By participating in our CuriousJr classes, you will not only improve your ability to solve challenging tasks but also strengthen your overall cognitive abilities. This empowers you to achieve more in less time making learning math an enjoyable and rewarding experience.What is Geometry?
Geometry is a branch of math that helps us understand shapes, sizes, and how they fit together. It’s all about learning about different shapes like circles, squares, triangles, and rectangles, and how they look, feel, and work.
Geometry helps us understand the space around us, like how to measure distances, angles, and areas.
Geometry FAQs
Where is geometry used in real life?
Geometry is used in architecture, interior design, and construction for stable and visually appealing structures. Navigation, maps, and route planning rely on geometry to calculate distances and plan efficient paths. Artists and designers apply geometric shapes and patterns for visual harmony in their works.
What is the smallest shape in geometry?
The smallest geometric shape is a point with no length, width, or height. However, it is used as the foundation for all other shapes. The largest regular polygon that can fit inside a circle is a hexagon. This means that a circle can be divided into six equal parts using only straight lines.
Who is the father of geometry?
Euclid
What is the main focus of geometry?
The branch of mathematics concerned with the shape of individual objects, spatial relationships among various objects, and the properties of surrounding space.
What is geometry proof?
A geometric proof is a method of determining whether a statement is true or false with the use of logic, facts and deductions. A proof is kind of like a series of directions from one place to another.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App