Physics Wallah

What are Length, Width, and Height: Key Differences with Examples

Length, width, and height are geometrical dimensions that define the size, shape, and structure of objects. Learn the real-life applications of length, width, and height here.
authorImageChandni 1 Aug, 2025
Share

Share

Length, Width, and Height

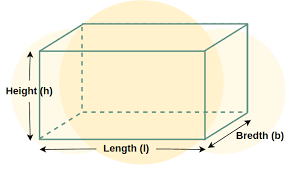
Length, Width, and Height: Dimensions shape how we interact with the world. At their core are length, breadth, and height, simple yet fundamental measurements. Length captures the longest side, like the span of a table.

Breadth or width measures the distance across, perpendicular to length. Height gauges how tall something stands, reaching vertically. Together, they define the size, space, and structure of everything around us, from boxes to buildings. Understanding these three dimensions helps us visualize, design, and organize with precision.

What Are Length, Width, and Height?

Length, width, and height are dimensions for measuring an object's size. In two-dimensional (2D) shapes, we use length and breadth. In three-dimensional (3D) shapes, we incorporate height along with length and width.  

Isosceles Triangle

Length

Length represents the longest horizontal measurement of an object. It tells us how long the object is from one end to the other. This dimension is used to determine the maximum extent of an object along a straight line. For example, in a rectangular table, the side that stretches the furthest is considered its length. Length is typically measured in units such as meters (m), centimeters (cm), millimeters (mm), inches (in), or feet (ft), depending on the context and scale of measurement. Length Examples
  • Measuring Furniture: When buying a sofa, you might measure its length to ensure it fits against your wall. For instance, a sofa might be 2 meters long .
  • Road Distances: The distance between two towns or cities is often described in kilometers. For example, "The length of the road from City A to City B is 150 km ."
  • Personal Height Measurement: When measuring a person’s height, the measurement represents the length of their body from head to toe.

Width ( Breadth)

Width , also called breadth , is the shorter horizontal measurement of an object, running perpendicular to the length. It measures how wide or broad the object is from side to side.

Width complements the length and is used when describing objects that are not just long but also have a breadth to them. Width is measured using the same units as length, such as meters, centimeters, inches, or feet .

Breadth Examples 

  1. Measuring a Table: If a table has a length of 2 meters and a width of 1 meter , the width tells us how broad the table is from side to side.
  2. Books and Notebooks: The width of a standard book might be 15 cm , while its length might be 25 cm .
  3. Smartphones: A phone with a width of 7 cm and a length of 15 cm indicates how broad the device is when held horizontally.

Height (Depth)

Height refers to the vertical measurement of an object, indicating how tall or deep it is. In some contexts, particularly when measuring downward, height is referred to as depth . Height is the dimension that runs perpendicular to both length and width. Common units for measuring height include meters (m), centimeters (cm), inches (in), and feet (ft).

Height Examples

  • Buildings: The height of a skyscraper might be 300 meters , indicating how tall the structure is from the ground to the top.
  • Swimming Pools: The depth of a swimming pool might be 2 meters , describing how deep the pool is from the surface of the water to the bottom.
  • Children's Growth: A child’s height might be measured at 120 cm , representing their vertical growth.

Perimeter of a Triangle

Length, Width, and Height Key Differences

To better understand these dimensions, let’s summarize the differences between length, width, and height:
Aspect Length Width (Breadth) Height (Depth)
Definition Longest horizontal dimension Shorter horizontal dimension Vertical dimension
Direction Horizontal, longest side Horizontal, shorter side Vertical (upward or downward)
Orientation Along the object's maximum extent Perpendicular to length Perpendicular to both length and width
Common Units m, cm, in, ft m, cm, in, ft m, cm, in, ft
Example Object Length of a table (e.g., 2 m) Width of a table (e.g., 1 m) Height of a table (e.g., 0.8 m)
Applications Measuring distance, furniture, roads Measuring screens, books, and doorways Measuring buildings, shelves, water depth

How Do Length, Width, and Height Work Together?

Length, width, and height work together to define a three-dimensional object’s size, volume, and surface area . For example, a box with dimensions 30 cm × 20 cm × 15 cm is 30 cm long , 20 cm wide , and 15 cm high . These dimensions help calculate:

Volume: Volume tells us how much space the object occupies, expressed in cubic units like cubic meters (m³), cubic centimeters (cm³), or cubic inches (in³).

The formula for the volume of a rectangular prism (cuboid) is: = Length × Width × Height

Surface Area: Surface area represents the total area required to cover the object's surfaces, expressed in square units like square meters (m²), square centimeters (cm²), or square inches (in²).

The formula for the surface area of a cuboid is = 2×(Length × Width + Length × Height + Width × Height)

Triangles

Example 1: Volume of a Rectangular Box

Imagine a rectangular box with the following dimensions:
  • Length: 15 cm
  • Width: 10 cm
  • Height: 5 cm
These measurements provide a complete description of the box:
  • The length (15 cm) tells us how long the box is.
  • The width (10 cm) shows how wide it is.
  • The height (5 cm) indicates how tall the box stands.
Together, these dimensions allow us to calculate the volume of the box using the formula:

Volume= Length × Width × Height

Substituting the values:

Volume = 15 cm × 10 cm × 5 cm = 750 cm 3

This means the box can hold 750 cubic centimeters of material.

Surface Area of a Rectangular Box

To calculate the surface area of the box, use the formula:

Surface Area = 2×(Length × Width + Length × Height + Width ×Height)

Substituting the values:

Surface Area=2×(15 cm ×10 cm +15 cm ×5 cm +10 cm ×5 cm)

Calculating each term:

15 ×10 = 150 cm 2 15 × 5 = 75 cm 2 10×5 = 50 cm 2

Adding them together:

150 + 75 + 50 = 275 cm 2 Now multiply by 2: 2 × 275 = 550 cm 2 The surface area of the rectangular box is 550 square centimeters. This represents the total area needed to cover all six faces of the box.

Example 2:  Finding the Missing Dimension

The volume of a cuboid is 144 cubic cm. The length is 12 cm, and the width is 2 cm. Find the height.

Solution:

Using the volume formula: Length × Width × Height Substituting the values, we get: 144 = 12 ×2 × Height

Simplify:

144 = 24 × Height Height = 144/24

Answer: The height of the cuboid is 6 cm .

Practical Applications of Length, Width, and Height

Let’s explore the real-life applications of length, width, and height:

Architecture and Construction

In construction projects, accurate measurements of length, width, and height are essential. For example, when designing a building, architects specify:
  • The length of walls and beams
  • The width of rooms and corridors
  • The height of ceilings and structures
These dimensions ensure that the structure is functional, safe, and aesthetically pleasing.

Packaging and Shipping

In logistics, understanding dimensions is critical for packaging and shipping. Companies measure the length, width, and height of boxes to:
  • Calculate the volume for shipping costs
  • Ensure products fit into packaging appropriately
  • Optimize storage space in warehouses

Interior Design

When arranging furniture in a room, designers consider:
  • The length of sofas, tables, and shelves
  • The width of doorways and walkways
  • The height of cabinets, curtains, and wall hangings
Length, width, and height are used to describe the size of 3D objects. Length is the longest horizontal side, width is the shorter horizontal side, and height is how tall the object is. Together, they help us understand the shape of an object, calculate how much space it takes up (volume), and complete tasks like designing spaces or packaging items. Join Online Classes for Kids now!!
Related Articles
Trapezium Area of a Circle
Prime Numbers Diameter of a Circle
Shapes Diameter of a Circle

Length, Width, and Height FAQs

Can an object have length but no breadth or height?

Theoretically, yes. A line has length but no measurable breadth or height, making it a one-dimensional figure.

How do changes in one dimension affect the overall volume of an object?

Increasing any one of length, breadth, or height increases the volume proportionally, while decreasing one reduces the volume.

Can two objects have the same volume but different lengths, breadths, and heights?

Yes. A tall, narrow box and a short, wide box can have the same volume but different dimensions.

What happens to the proportions of an object if you double its length, breadth, and height?

Doubling all three dimensions increases the volume by a factor of eight, demonstrating exponential growth in space occupied.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.