
Trapezium (known as a trapezoid in the United States) is a fascinating and widely used geometric shape in both mathematics and everyday life. Whether you’re studying geometry or curious about its practical applications, understanding the trapezium is essential. This comprehensive blog will explore the definition, types, properties, and formulas of a trapezium, alongside real-world examples.
What is Trapezium?
Trapezium is a 2D quadrilateral with only one pair of opposite sides that are parallel. Unlike squares and rectangles, which have two pairs of parallel sides, a trapezium's defining characteristic is this single set of parallel sides.
Basic Trapezium Characteristics:
- Four sides (making it a quadrilateral).
- Two parallel sides (called the bases).
- Four angles that together sum up to 360° .
- Non-parallel sides are often referred to as legs .
In the trapezium figure given below, the parallel sides are denoted as ‘a’ (the shorter base) and ‘b’ (the longer base), while the distance between these parallel sides is called the height (h) .
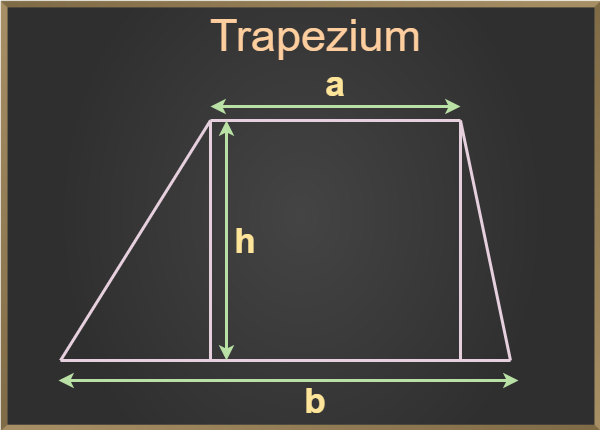
Properties of Trapezium
Here are the different properties of trapezium:
- A trapezium is defined by having only one pair of opposite sides that are parallel. These parallel sides are referred to as the bases. The other two sides, known as the legs, are not parallel and can differ in length.
- The interior angles of a trapezium always add up to 360° . This rule applies to all quadrilaterals, including trapeziums, due to their four-sided nature.
- In a trapezium, the adjacent angles between each leg and the bases are supplementary . This means that the sum of these adjacent angles equals 180° . For example, if one angle measures 110°, the adjacent angle on the same leg will measure 70°.
- The diagonals of a trapezium can vary; they are equal in length in an isosceles trapezium and typically different in length in a scalene trapezium.
- In an isosceles trapezium , the base angles are equal . This symmetry occurs because the non-parallel sides (legs) are of equal length. For example, if one base angle measures 60° , the adjacent base angle on the opposite side will also measure 60° . This property helps in solving angle-related problems and recognizing symmetry in the shape.
- A right trapezium features two angles that are exactly 90° . These right angles occur where one leg meets the two bases perpendicularly. This makes calculations involving the height, area, and perimeter straightforward, as the leg with the right angles also serves as the height of the trapezium.
Types of Trapezium
Trapeziums come in various forms, each with distinct characteristics that make them unique. Understanding these variations helps in identifying and working with them in different mathematical and real-world contexts. The three primary types of trapeziums are Isosceles Trapezium , Right Trapezium , and Scalene Trapezium. Let’s explore each type in detail.
Isosceles Trapezium
An Isosceles Trapezium is a special type of trapezium where the non-parallel sides, also known as the legs, are of equal length . This equality of the legs gives the trapezium a symmetrical appearance, making it easier to identify.
Properties of an Isosceles Trapezium
- Equal Base Angles : The angles adjacent to each base are equal. This symmetry helps in solving geometric problems involving angles.
- Equal Diagonals : The diagonals (lines connecting opposite corners) of an isosceles trapezium are of equal length. This property is useful when calculating the dimensions or area of the trapezium.
- Symmetrical Shape : The isosceles trapezium exhibits symmetry along the perpendicular bisector of the parallel sides.
Example : If the parallel sides are 6 cm and 10 cm, and the non-parallel sides (legs) are each 5 cm, the trapezium is isosceles because the legs are equal.
Right Trapezium
A Right Trapezium is characterized by having at least one right angle (90°) . This type of trapezium simplifies many calculations because the presence of right angles allows the use of straightforward geometric formulas.
Properties of a Right Trapezium
- Two Right Angles : The two adjacent angles on one of the legs are exactly 90°, making one leg perpendicular to the bases.
- Simplified Calculations : The presence of right angles makes it easier to calculate the area and perimeter of the trapezium since standard right-angle geometry principles apply.
- Straightforward Height Measurement : In a right trapezium, the leg that forms the right angle with the bases also serves as the height, simplifying height determination.
Example : If one base measures 8 cm, the other base measures 5 cm, and the leg forming a right angle is 6 cm, the trapezium is classified as a right trapezium due to the 90° angles.
Scalene Trapezium
A Scalene Trapezium is a trapezium where no sides or angles are equal . This type lacks symmetry and regularity, making it the most irregular form of a trapezium.
Properties of a Scalene Trapezium
- No Equal Sides : All four sides of a scalene trapezium have different lengths, unlike the isosceles or right trapezium.
- No Equal Angles : The angles in a scalene trapezium vary in measure, and none are necessarily equal.
- Asymmetrical Shape : The shape does not exhibit any symmetry, making it more challenging to work with geometrically.
Example : If the bases measure 7 cm and 4 cm, and the legs measure 5 cm and 6 cm, the trapezium is scalene because all sides are of different lengths and the angles differ.
Trapezium Formulas
To work with trapeziums effectively, here are essential formulas for calculating the area and perimeter.
Area of a Trapezium
The formula for the area of a trapezium is:
Area=1/2×(a+b)×h
Where:
a = length of the shorter base
b = length of the longer base
h = height (distance between the parallel sides)
Example
If a = 4 cm , b = 8 cm , and h = 5 cm , the area is:
Area=1/2×(4+8)×5 =1/2 × 12 × 5=30 cm 2
Perimeter of a Trapezium
The formula for the perimeter of a trapezium is the sum of the lengths of all four sides:
Perimeter=a+b+c+d
Where c and d are the lengths of the non-parallel sides (legs).
Example:
If a = 4 cm , b = 8 cm , c = 5 cm , and d = 6 cm , the perimeter is:
Perimeter=4+8+5+6=23 cm
Real-World Applications of Trapeziums
Trapeziums aren’t just abstract shapes in a textbook—they appear in various practical contexts. Here are some real-world examples where trapeziums play a crucial role:
Architecture and Construction
Roofs : Many sloped roofs are shaped like trapeziums, providing stability and an efficient way to manage rainwater runoff.
Bridges : The side profiles of many bridges often resemble trapeziums, helping distribute weight evenly.
Everyday Objects
Handbags and Purses : Many bags are designed in a trapezium shape for style and functionality.
Popcorn Buckets : The classic cinema popcorn bucket often has a trapezium shape, wider at the top and narrower at the base.
Geometry and Design
Windows and Door Frames : Certain architectural designs incorporate trapezium-shaped windows or door panels for aesthetic appeal.
Lampshades : Many lampshades, when viewed as 2D projections, take the form of trapeziums.
Differences Between Trapezium and Other Quadrilaterals
Understanding the differences between a trapezium and other quadrilaterals can help avoiconfusion.n:
Trapezium vs. Parallelogram
- Trapezium : Only one pair of opposite sides is parallel.
- Parallelogram : Both pairs of opposite sides are parallel.
Trapezium vs. Rectangle
- Trapezium : Non-parallel sides can have different lengths and angles.
- Rectangle : Opposite sides are parallel and equal, with all angles at 90° .
Trapezium vs. Square
- Trapezium : Only one set of parallel sides.
- Square : All sides are equal, with all angles at 90° .
The trapezium is an incredibly versatile shape with applications in mathematics, engineering, design, and everyday life. By understanding its properties, types, and formulas, you can solve a wide range of problems and appreciate its real-world significance. Whether you're calculating areas for a math problem or identifying shapes in your surroundings, the trapezium is a fundamental geometric figure that proves both practical and intriguing.
Join Online Maths Classes for Kids Now!!
|
Related Articles |
|
| Percentage | Surface Area of Cylinder |
| Square 1 to 30 | Square Root |
| Roman Numerals 1 to 100 | Compound Interest |
Trapezium FAQs
Can a trapezium have all sides of different lengths?
How do you determine if a given quadrilateral is a trapezium?
Is it possible for a trapezium to have two equal non-parallel sides but different base angles?
Can a trapezium have three right angles?
Can a trapezium be divided into simpler shapes for calculation purposes?
Do all trapeziums have symmetrical properties?









