Triangles: Parts, Angles, Perimeter, Area Properties, and Types
A triangle in geometry is a three-sided polygon defined by three vertices and three angles. Understand the properties and types of triangles based on their side lengths and angles.
Chandni 23 Dec, 2024
Share
Triangles are fascinating shapes found everywhere, from nature to architecture. But what exactly is a triangle in geometry? A triangle is a three-sided polygon with three edges and three vertices.
One of its key properties is that the sum of its three interior angles is always 180 degrees, known as the angle sum property .Triangles come in different types, such as equilateral, isosceles, and scalene, depending on the lengths of their sides.
They are often labeled as ∆ABC, where A, B, and C are the vertices. Read on to learn more about triangles!
What is a Triangle ?
A triangle is a three-sided polygon, where each side is a straight line segment. The points where two sides meet are called vertices; each vertex forms an angle. Triangles are classified by their angles (acute, right, obtuse) and sides (equilateral, isosceles, scalene). [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1-1.mp4"][/video]Parts of a Triangle
A triangle consists of three sides, three angles, and three vertices. In triangle XYZ, the sides are XY, YZ, and ZX. The angles are formed where two sides meet, denoted by the symbol ∠. The three angles in triangle XYZ are ∠XYZ, ∠YZX, and ∠ZXY, also referred to as ∠X, ∠Y, and ∠Z, respectively. The vertices are the points where two sides intersect, which in triangle XYZ are X, Y, and Z. These components together define the structure of a triangle.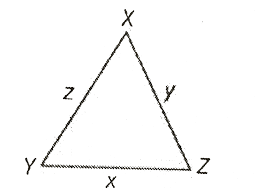
Properties of Triangle
Triangles have several important properties, including the following, that make them fundamental in geometry: Sum of Interior Angles : The sum of the three interior angles of any triangle is always 180 degrees. For example, in triangle XYZ, if ∠X = 60°, ∠Y = 70°, and ∠Z = 50°, their sum equals 180°. Triangle Inequality Theorem: The sum of the lengths of any two sides of a triangle is always greater than the length of the third side. For instance , if a triangle has sides XY, YZ, and ZX, then XY + YZ > ZX. Side Difference Property : The difference between the lengths of any two sides of a triangle is always less than the length of the third side. Using the same triangle, |XY - YZ| < ZX. Similarity of Triangles: Two triangles are considered similar if their corresponding angles are equal (congruent) and their corresponding side lengths are proportional. This means that if triangle ABC and triangle XYZ have ∠A = ∠X, ∠B = ∠Y, and ∠C = ∠Z, and the ratio of their sides AB/XY = BC/YZ = CA/ZX, the triangles are similar.Types of Triangles
Triangles can be classified in two major ways: based on the length of their sides and based on the measure of their angles. This results in six distinct types of triangles. Let’s explore each classification in detail.Based on the Length of the Sides:
Scalene Triangle: In a scalene triangle, all three sides have different lengths. No sides are equal, and all angles are also different from each other. Isosceles Triangle: An isosceles triangle has two sides of equal length, and the angles opposite these sides are also equal. The third side is of a different length, making this triangle symmetrical along the axis through the two equal sides. Equilateral Triangle: An equilateral triangle has all three sides of equal length. Additionally, all three angles are equal, each measuring 60 degrees, making it also an acute triangle.Based on the Angles:
Acute Angle Triangle: An acute angle triangle has all three angles less than 90 degrees. These triangles are sharp and have no right angles or obtuse angles. Obtuse Angle Triangle: An obtuse angle triangle has one angle that is greater than 90 degrees but less than 180 degrees. The other two angles in the triangle will be acute (less than 90 degrees) Right Angle Triangle: A right angle triangle has one angle exactly equal to 90 degrees. The side opposite the right angle is the longest side, called the hypotenuse, while the other two sides are the legs of the triangle. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]Angles of Triangle
A triangle has three angles, each formed where two sides meet at a point called the vertex. The sum of these three interior angles is always 180°. If we extend the sides of the triangle outward, exterior angles are formed. Each interior angle and its adjacent exterior angle add up to 180°. Let’s say the interior angles are ∠1, ∠2, and ∠3, and their corresponding exterior angles are ∠4, ∠5, and ∠6.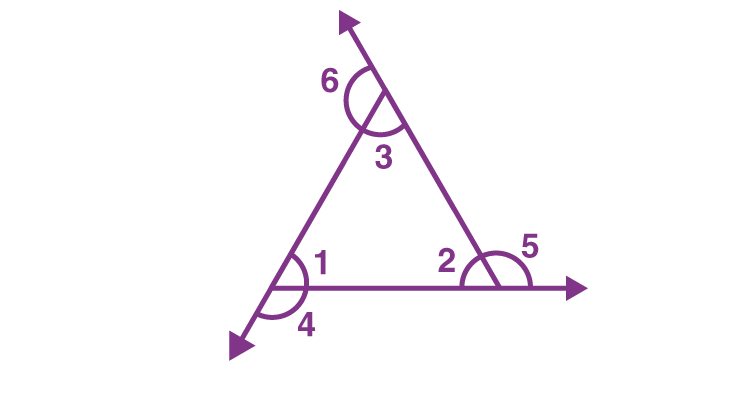
This gives us:
- ∠1 + ∠4 = 180°
- ∠2 + ∠5 = 180°
- ∠3 + ∠6 = 180°
Perimeter of a Triangle
The perimeter of a triangle is the total length around the triangle, calculated by adding the lengths of all three sides. It represents the boundary of the triangle. The perimeter is expressed in the same unit as the side lengths, whether in centimeters, meters, or any other unit of length.Perimeter of a Triangle Formula
If a triangle has sides of lengths AB, BC, and AC, the perimeter (P ) of the triangle is simply the sum of these three side lengths: Perimeter= AB+ BC+ AC For example, if a triangle has side lengths of 5 cm, 7 cm, and 8 cm, the perimeter would be: Perimeter = 5 + 7 + 8 = 20 cmArea of a Triangle
The area of a triangle refers to the amount of space enclosed within its boundaries. The area depends on the triangle’s base and height, and it is measured in square units, such as square centimeters or square meters.Area of a Triangle Formula (when Base and Height are known):
The area of a triangle can be calculated if we know the base (B) and the height (H) . The formula for the area is: Area =½ × Base × Height This formula works for all types of triangles, provided the base and the corresponding height are known.Example:
Let’s say we have a triangle with a base of 9 cm and a height of 6 cm. Using the formula: Area =½ × 9 × 6 = 27cm 2 Thus, the area of the triangle is 27 square centimeters.Area of a Triangle Using Heron’s Formula
In some cases, the base and height of the triangle are not provided. If we know the lengths of all three sides of the triangle, we can still calculate the area using Heron’s formula . To calculate the area of a triangle using Heron’s formula, we first need to determine the semi-perimeter (s) of the triangle. The semi-perimeter is half of the perimeter and can be calculated as: s= a + b + c / 2 Here a , b , and c are the lengths of the sides of the triangle. After calculating the semi-perimeter, the area ( A ) of the triangle can be found using the following formula:A= s(s−a)(s−b)(s−c)
Where:- s is the semi-perimeter,
- a , b , and c are the sides of the triangle.
| Related Articles | |
| Trapezium | Area of a Circle |
| Prime Numbers | Diameter of a Circle |
| Shapes | Diameter of a Circle |
Triangle FAQs
If a triangle has two sides measuring 8 cm and 10 cm, how do you determine the possible length of the third side?
The length of the third side must be greater than the difference of the other two sides (10 - 8 = 2 cm) and less than their sum (8 + 10 = 18 cm). Therefore, the third side must be between 2 cm and 18 cm.
What does it mean for a triangle to be equiangular?
An equiangular triangle is a triangle where all three angles are equal, meaning each angle measures 60°, making it also an equilateral triangle.
How do you find the height of a triangle if only the area and base are known?
You can rearrange the area formula for a triangle: Area = 1/2 × Base × Height. Solving for height, Height = (2 × Area) / Base.
What is a right-angled isosceles triangle?
A right-angled isosceles triangle has one 90° angle and the two other angles are 45° each. The two sides adjacent to the right angle are of equal length.
What is the relationship between the sides of a 30-60-90 triangle?
In a 30-60-90 triangle, the lengths of the sides are in a consistent ratio: the side opposite the 30° angle is half the length of the hypotenuse, and the side opposite the 60° angle is √3 times the shorter leg.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.