Parabola Equations, Formulas, Graphing, and Examples
A parabola is a U-shaped curve that represents the graph of a quadratic function. Check out parabola derivations, equations, and formulas with examples to understand this shape better.
Chandni 31 Jul, 2025
Share
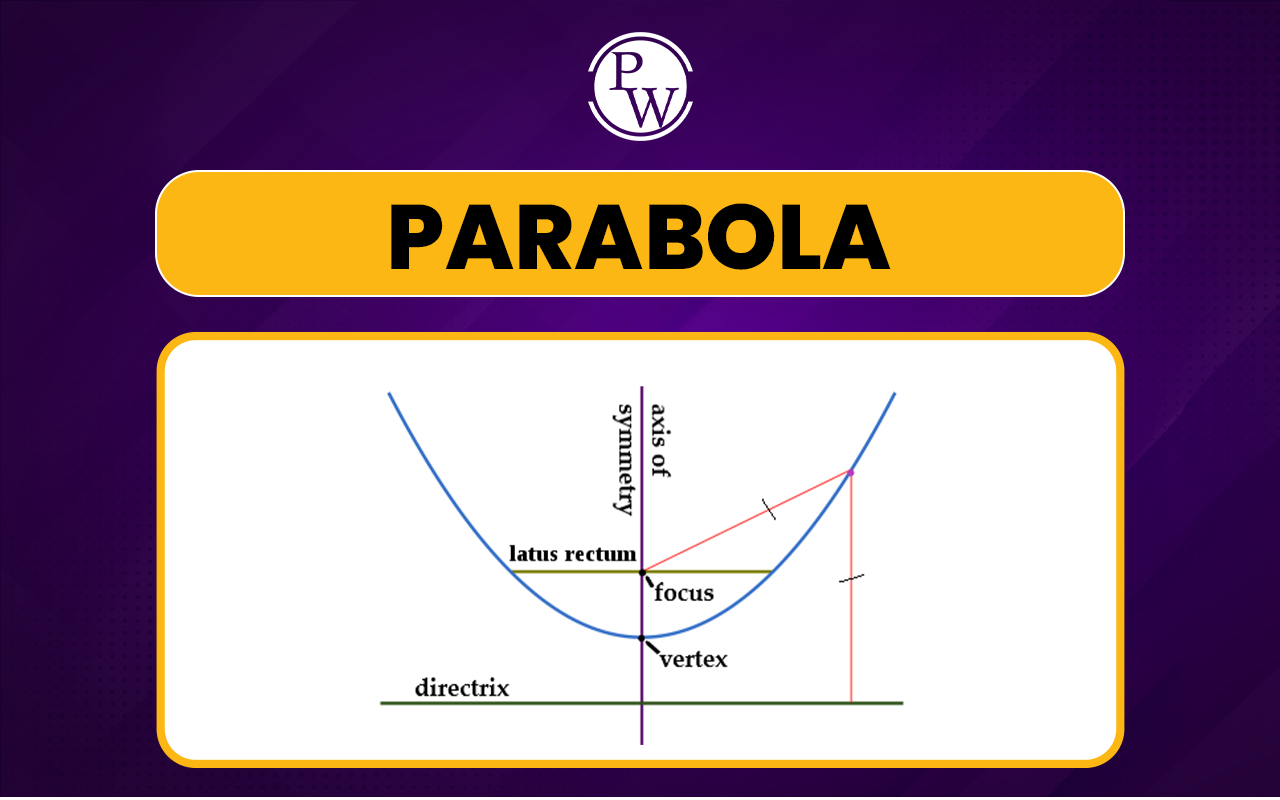
A Parabola is an approximately U-shaped symmetrical curve formed on a two-dimensional plane. The shape also resembles the curvilinear path of many objects in motion when they move upward and fall under the effect of gravity.
When you kick a soccer ball or throw a stone, the path is shaped like a parabola. In mathematics, the shape of this curve or parabola can be derived using certain conditions. In this article, we will clarify the concepts of parabola, its different forms, and the essential elements related to it. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]What is a Parabola?
A parabola is a curved shape on a two-dimensional plane. It is formed by moving a point so that its distance from a fixed point and a fixed line are always equal. This means any point on this curve is of equal distance from a point and a straight line.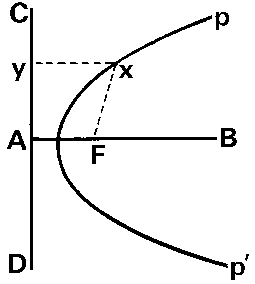
In this image, pp’ is a curve such that any point x on it is equidistant from a fixed-point F and the straight-line CD. More specifically, the distance of the point x on the curve from F and any point y on the line are equal. This condition satisfies the criteria of a parabola, so we can say that pp’ is a parabola. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]
Important Components of Parabola
The important terms relevant to the concept of parabola are mentioned as follows:- Focus: The fixed point from which the distance of any point of the parabola remains constant is called the Focus (F)
- Directrix: The perpendicular line from which the distance of any point of the parabola remains constant is called Directrix.
- Focal Chord: The focal chord of a parabola is the line passing through the parabola's focus and cutting the parabola at two distinct points.
- Axis: It is the straight line passing through the parabola's focus and perpendicular to the Directrix.
- Vertex: The point of intersection of the axis and the parabola. It is denoted by V.
- Latus Rectum : The focal chord of the parabola that is perpendicular to the axis and passes through the focus.
- Focal Distance : The distance of any point on the parabola from the focus is called the focal distance or focal length. It is also the perpendicular distance of the vertex from the directrix.
- Eccentricity : It is the ratio of the distance of a point on the parabola from the focus to the distance of the same point from the Directrix. It is denoted by e. For a parabola, e is always equal to 1.
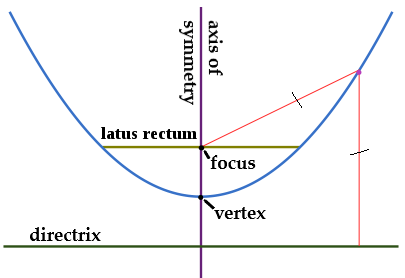
General Equation of Parabola
The general equation of a parabola can be given as:- y = a (x - h) 2 + k
- x = a (y - k) + h 2
Parabola Formulas
The parabola formula is used to describe the general equation and properties of a parabola in a plane. It provides the necessary equations to calculate various parameters, such as its vertex, axis of symmetry, focus, and directrix. Below are the formulas commonly used to determine the parameters of a parabola.|
Parabola Formulas |
||
| Parabola Equation | y = a (x - h) 2 + k | x = a (y - k) + h 2 |
| Axis of Symmetry | x = h | y = k |
| Vertex | (h, k) | (h, k) |
| Focus | (h, k + (1/4a)) | (h + (1/4a), k) |
| Directrix | y = k - 1/4a | x = h - 1/4a |
| Direction of Opening | Up (for a > 0) or Down (for a < 0) | Right (for a > 0) or Left (for a < 0) |
Standard Equation of Parabola
The standard equation of a parabola can be of four types, as follows:- y 2 = 4ax
- y 2 = -4ax
- x 2 = 4ay
- x 2 = -4ay
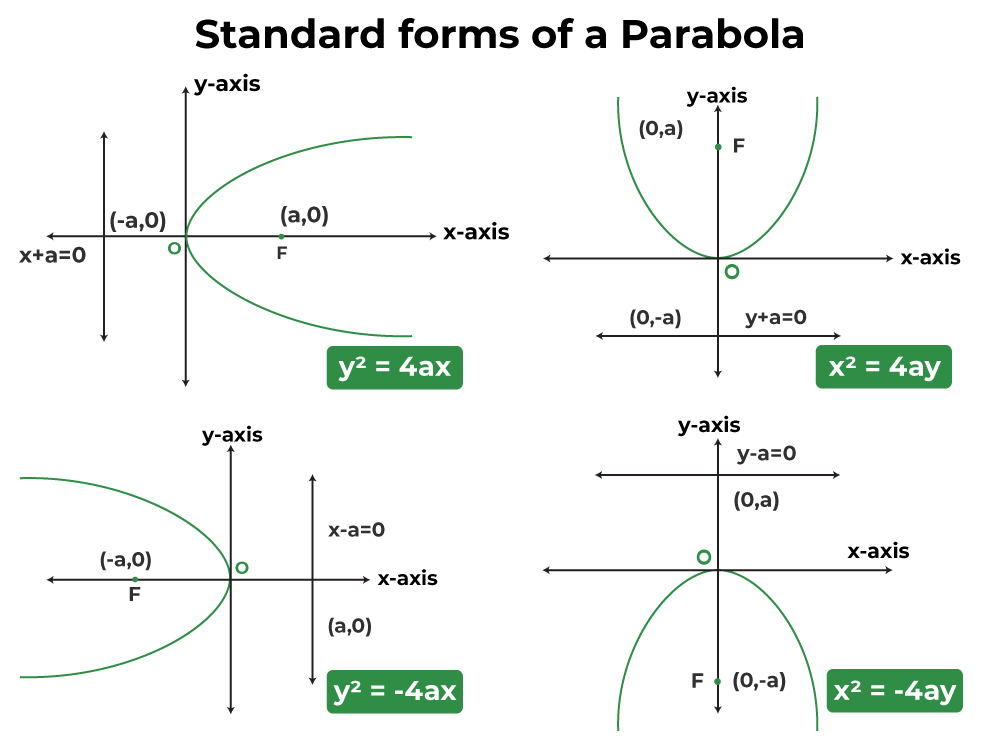The four standard equations generate four forms of parabola based on the axis and the orientation of the parabola. The axis and the directrix of each of these parabolas are different. The following are the observations made from the standard form of equations:
- If the equation has the term y 2 , then the axis of symmetry is along the x-axis.
- If the equation has the term x 2 , then the axis of symmetry is along the y-axis.
- When the axis of symmetry is along the x-axis and the coefficient of the x is positive, the parabola opens to the left.
- When the axis of symmetry is along the x-axis and the coefficient of the x is negative, the parabola opens to the right.
- When the axis of symmetry is along the y-axis, the parabola opens upwards if the coefficient of y is positive.
- When the axis of symmetry is along the y-axis, the parabola opens downwards if the coefficient of y is negative.
|
Various Forms of a Parabola |
||||
| Equation of parabola | y 2 = 4ax | y 2 = -4ax | x 2 = 4ay | x 2 = -4ay |
| Equation of axis | y = 0 | y = 0 | x = 0 | x = 0 |
| Equation of directrix | x + a = 0 | x -a = 0 | y + a = 0 | y – a = 0 |
| Vertex | (0,0) | (0,0) | (0,0) | (0,0) |
| Focus | (a, 0) | (-a, 0) | (0, a) | (0, -a) |
| Length of Latus Rectum | 4a | 4a | 4a | 4a |
| Direction of Opening | Right | Left | Upward | Downward |
Parabola Equation Derivation
Take a fixed point with coordinates (a, 0), which is the focus (F). The directrix is a straight line parallel to the y-axis with the equation x + a = 0. Take a point P with coordinates (x, y) on the parabola. As per the definition of a parabola, the distance of point P from the focus F is equal to the distance of point P from the directrix. Here, we consider a point C on the directrix so that PC = PF.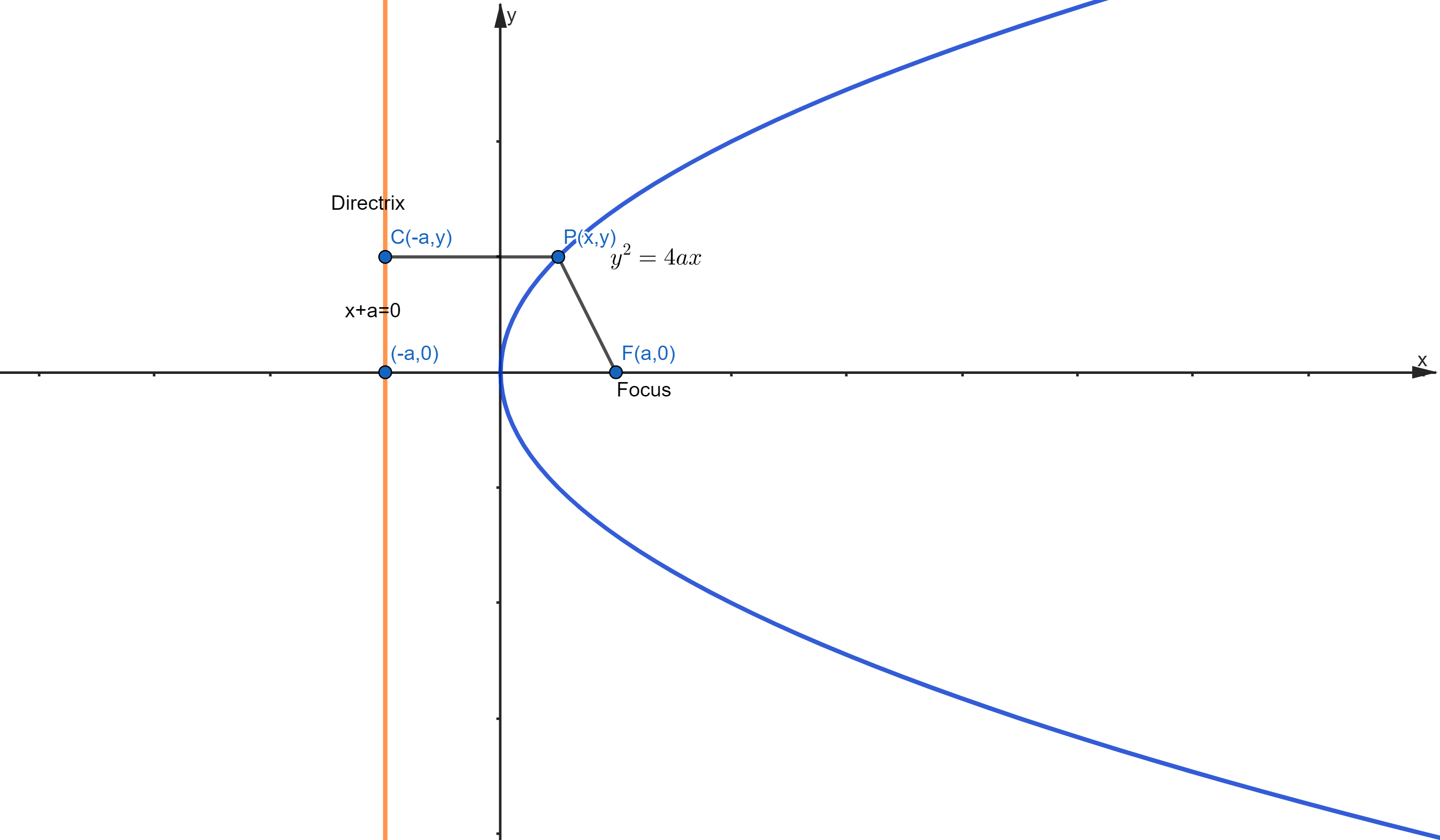
Using the distance formula, we can write, PF = √ {(x – a) 2 + y 2 } Also, PC = √ (x + a) 2 Since PF = PC, we get √ {(x – a) 2 + y 2 } = √ (x + a) 2 So by squaring both sides, we have (x – a) 2 + y 2 = (x + a) 2 or, x 2 – 2ax + a 2 + y 2 = x 2 + 2ax + a 2 or, y 2 = 4ax Therefore, we can say that any point on the parabola with a positive x coordinate satisfies this equation.
Tangent to a Parabola
A tangent is a line touching the parabola at a single point. The equation of a tangent to a parabola y 2 = 4ax is y = mx + c, where c = a/m. Some of the essential terms related to the tangent of a parabola are as follows:- Normal : The line perpendicular to the tangent, passing through the point of contact, and the parabola's focus.
- Chord of Contact: The chord joining the point of contact of the tangents drawn from an external point to the parabola is called the chord of contact.
Parabola Solved Examples
Find the coordinates of the focus, the equation of the directrix, and the measure of the latus rectum of the parabola y 2 = 12x
Solution:
From the given parabola equation, the axis is along the x-axis. The coefficient of x is positive, so it opens to the right. By comparing y 2 = 12x with equation y 2 = 4ax, we get a = 3. Therefore, the parabola's focus coordinates are (3, 0). The equation of the directrix is x = -a. By replacing the value of a, we get the equation of directrix as x = -3 or x + 3 = 0 Also, the length of the latus rectum is 4a = 4 x 3 = 12 The parabola is a geometrical curve on a plane with some distinct properties and can be seen in real life in moving objects. The concept of parabolas is used in many calculations concerning the practical applications of physics and engineering.| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Differentiation |
| Perimeter of Rectangle | Surface Area of Cylinder |
Parabola FAQs
What is a parabola in mathematics?
A parabola is a U-shaped curve that is the graph of a quadratic function or the locus of points equidistant from a fixed point (focus) and a fixed line (directrix
What is the axis of symmetry in a parabola?
The axis of symmetry is the vertical or horizontal line that passes through the vertex, dividing the parabola into two mirror images.
How is a parabola used in physics and engineering?
Parabolas are used in reflecting light and sound (parabolic mirrors), designing projectile motion, and constructing bridges and satellite dishes.
What is the difference between an ellipse, a hyperbola, and a parabola?
A parabola has one focus and one directrix. An ellipse has two foci and is a closed curve, while a hyperbola has two foci and two separate branches.
How is the parabola concept used in fountains?
The water shoots of the fountain move up in the air and fall following a parabolic path, making it attractive.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
