
Place Value: Have you ever noticed how a number changes depending on where its digits are? For example, in 25, the 2 means twenty, but in 205, it means two hundred. This happens because of place value, which tells us the value of a digit based on its position in a number.
Place value helps us read, write, and understand numbers, whether they’re small or very large. Imagine it as each digit having a special role, like ones, tens, or hundreds, depending on where it stands. In this blog, we will explore the concept of place value in detail, focusing on how it works in both the Indian and international numbering systems.What is Place Value?
So, what is the place value? Place value is the value a digit holds depending on its position in a number. Each position has a specific value, starting from ones, tens, hundreds, thousands, and so on as we move left. For example, in the number 7,853 :- The digit 3 is in the ones place, so its value is 3×1=3
- The digit 5 is in the tens place, so its value is 5×10=50
- The digit 8 is in the hundreds place, so its value is 8×100=800
- The digit 7 is in the thousands place, so its value is 7×1,000=7,000
This is a perfect place value example that shows how digits change their value depending on where they are.
In another example, for the number 31,204 :- The digit 3 is in the ten thousands place, so its value is 3×10,000=30,000
- The digit 1 is in the thousands place, so its value is 1×1,000=1,0001
- The digit 2 is in the hundreds place, so its value is 2×100=200
- The digit 0 is in the tens place, so its value is 0×10=0
- The digit 4 is in the ones place, so its value is 4×1=4
Even if a digit is zero, its place value still depends on its position. And don’t worry even a zero plays a role in big numbers.
This shows how a digit’s value changes based on its position, even if the digit itself remains the same.Properties of Place Value
- The place value of a single-digit number is the same as its face value.
- The place value increases by ten times as you move one position to the left in a number.
- The place value of zero is always zero, regardless of its position. For example, in 405, the place value of the 0 is 0.
- As we move left in a number, the place value of each position increases by 10 times. For example, in 2,345, the place value of 3 (hundreds) is ten times the place value of 4 (tens).
Place Value Chart
A place value chart is a structured tool used in mathematics that helps organize the digits in a number based on their position. Each position in the chart represents a place value, such as ones, tens, hundreds, thousands, and so on. It makes it easy to see what each digit in a number stands for. Let’s use this concept to explain the Indian and International Place Value Systems and write numbers in expanded form.Indian Place Value System
The Indian place value chart helps organize numbers according to the Indian numbering system, making it easier to understand, read, and write large numbers. Each digit in a number has a specific place value, which is determined by its position from right to left. The chart divides numbers into periods, separated by commas, following the Indian format. For example, the number 13,10,46,914 can be broken down as:| Indian Place Value Chart | ||||||||
|---|---|---|---|---|---|---|---|---|
| Ten Crores (10,00,00,000) | One Crore (1,00,00,000) | Ten Lakhs (10,00,000) | One Lakh (1,00,000) | Ten Thousands (10,000) | Thousands (1,000) | Hundreds (100) | Tens (10) | Ones (1) |
| 1 | 3 | 1 | 0 | 4 | 6 | 9 | 1 | 4 |
Structure of the Indian Place Value Chart
- First Period : Includes three places—ones, tens , and hundreds .
- Second Period : Includes two places—thousands and ten thousands .
- Third Period : Includes two places—lakhs and ten lakhs .
- Fourth Period : Includes two places—crores and ten crores .
Decimal Numbers in the Indian Place Value Chart
For numbers with decimals, the positions after the decimal point are defined from left to right . For instance, in 45.789 :- 7 is in the tenths place, valued at 7 × 0.1=0.77
- 8 is in the hundredths place, valued at 8 × 0.01 = 0.088.
- 9 is in the thousandths place, valued at 9 × 0.001=0.0099
International Place Value System
The international place value chart organizes numbers into groups called periods : ones, thousands, and millions. Each period contains three places: ones, tens, and hundreds. Commas are used to separate these periods, making large numbers easier to read and write. For example, let’s consider the number 987,654,321 .| International Place Value Chart | ||||||||
|---|---|---|---|---|---|---|---|---|
| Hundred Millions (100,000,000) | Ten Millions (10,000,000) | Millions (1,000,000) | Hundred Thousands (100,000) | Ten Thousands (10,000) | Thousands (1,000) | Hundreds (100) | Tens (10) | Ones (1) |
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Place Value Examples from Real Life
Let’s take some fun place value examples from daily life:
If a pencil costs ₹20 and you buy 2, the total is ₹40. The digit 4 in 40 is in the tens place.
In your math notebook, page 105 has the digit 1 in the hundreds place. That means 1×100 = 100.
By looking around, you’ll spot the place value of numbers everywhere.
Fun Ways to Learn Place Value
Here are some fun tips:
-
Use color-coded blocks to understand the place value chart.
-
Play board games like Snakes and Ladders with number reading challenges.
-
Watch animated videos explaining what is the place value of digits.
These activities make learning the place value super easy and fun.
Why Is Place Value Important?
Without place value, we wouldn't be able to:
-
Read big numbers
-
Add or subtract correctly
-
Solve word problems
-
It’s the base of all math work.
Understanding the place value definition helps you become a math champ.
Comparison Between Indian and International Place Value Systems
- A 6-digit number is read as 1 lakh in the Indian system but as 100 thousand in the International system.
- A 7-digit number is read as 10 lakhs in the Indian system but as 1 million in the International system.
- For 8-digit numbers, 1 crore in the Indian system is equivalent to 10 million in the International system.
- For 9-digit numbers, 10 crores in the Indian system is equivalent to 100 million in the International system.
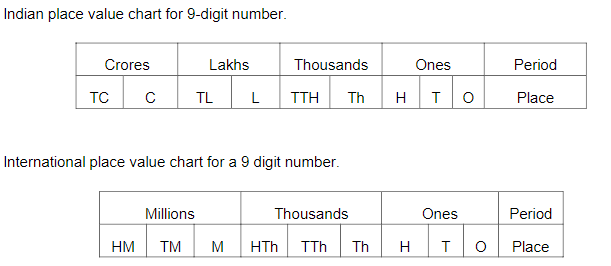
Difference Between Indian and International Place Value Chart
The Indian and International place value charts differ in how they group and organize numbers into periods, as well as in their use of commas and naming conventions. The table below highlights these differences:| Difference Between Indian and International Place Value Chart | ||
| Aspect | Indian Place Value Chart | International Place Value Chart |
| Number of Periods | 4 periods: ones, thousands, lakhs, and crores. | 3 periods: ones, thousands, and millions. |
| Period After Thousands | The period "lakhs" follows "thousands." | The period "millions" follows "thousands." |
| Comma Placement | Follows the 3:2:2 system: the first comma after three digits from the right, and subsequent commas after every two digits. | Follows the 3:3:3 system: commas placed after every three digits from the right. |
| Names of Places | Ones, tens, hundreds, thousands, ten thousands, lakhs, ten lakhs, crores, and ten crores. | Ones, tens, hundreds, thousands, ten thousands, millions, ten millions, and hundred millions. |
| Usage | Primarily used in India, Bangladesh, and Pakistan. | Used globally in most countries. |
Difference Between Place Value and Face Value
The difference between place value and face value lies in how the value of a digit is interpreted in a number. The face value of a digit is simply the digit itself, regardless of its position. For example, in the number 7,432, the face value of 7 is 7, the face value of 4 is 4, and so on. Face value remains constant no matter where the digit appears in the number. On the other hand, the place value of a digit depends on its position in the number and represents the value the digit contributes to the overall number. It is calculated as the digit multiplied by the positional value. For example, in the same number 7,432, the place value of 7 is 7×1,000 = 7,000, the place value of 4 is 4×100 = 400, the place value of 3 is 3×10 = 300, and the place value of 2 is 2×1 = 22. While the face value remains unchanged, the place value varies based on the digit's position.Place Value Solved Examples
Example 1: Determine the place value of the digit 5 in the number 94,560. In the number 94,560 , the digit 5 is in the hundreds place . The place value is: 5×100=500 Hence, the place value of 5 is 500 (five hundred). Example 2: Express the given numbers in both numerical and expanded forms. Thirty-one thousand five hundred and twenty-seven : Numerical form : 31,527 Expanded form : 30,000+1,000+500+20+730,000 + 1,000 + 500 + 20 + 730,000+1,000+500+20+7 Sixteen thousand four hundred and sixty-eight : Numerical form : 16,468 Expanded form : 10,000+6,000+400+60+810,000 + 6,000 + 400 + 60 + 810,000+6,000+400+60+8 Example 3: Given a number with 5 thousands, 9 hundreds, and 7 tens, determine the number.- 5×1,000=5,000
- 9×100=900
- 7×10=70
Adding the values:
5,000+900+70=5,9705,000 + 900 + 70 = 5,9705,000+900+70=5,970 The number is 5,970 . Example 4: Determine the place value of the digit 3 in the number 8.34. In the number 8.34, the digit 3 is in the tenths place. The place value is: 3×0.1=0.33 Hence, the place value of 3 is 0.3 (three-tenths).| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| What is an Abacus? | Math Puzzles |
| Multiplication Worksheets | Multiplication Sums |
Place Value FAQs
How is expanded form related to place value?
How does place value help in number comparison?
What is the connection between place value and rounding numbers?
Why do we start from the right in place value charts?
What happens if a digit's place value is misinterpreted?


