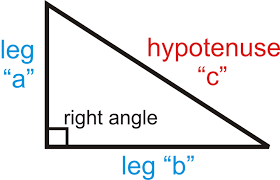
Pythagoras Theorem: Formula, Proof, and Solved Examples
The Pythagoras Theorem states the hypotenuse squared equals the sum of squares of two sides. Learn the proof of Pythagoras Theorem with a solved example here.
Chandni 7 Jan, 2025
Share
Pythagoras Theorem: A triangle with one right angle (90°, marked by a small square) is called a right triangle. The longest side, opposite the right angle, is known as the hypotenuse, while the two shorter sides are referred to as the legs, commonly labeled as "a," "b," and "c," where "c" represents the hypotenuse.
The Pythagorean Theorem establishes the relationship between these sides, making it one of the most significant principles in mathematics. Though named after the Greek mathematician Pythagoras, this theorem was applied by ancient civilizations like the Babylonians and Egyptians long before his time.
It remains a fundamental concept in geometry, widely used in fields such as construction, navigation, and design. Read this article to understand the concept of the Pythagorean Theorem in detail.
[video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]What is the Pythagoras Theorem?
Suppose you are building a ladder for a treehouse and need to figure out how long it should be. You already know the tree is 3 feet tall, and the base of the ladder sits 4 feet away from the tree. But how do you calculate the ladder’s length accurately without just guessing? This is exactly where Pythagoras' Theorem comes in. Pythagoras' Theorem states that in a right-angled triangle, the square of the longest side (called the hypotenuse) is equal to the sum of the squares of the other two sides. Mathematically, it’s expressed as: a 2 + b 2 = c 2 Here’s what these terms mean:- a and b are the two shorter sides of the triangle.
- c is the hypotenuse, the longest side opposite the right angle.
Now, let’s apply this theorem to our treehouse ladder problem!
- One side of the triangle (a) is 3 feet (the height of the tree).
- The other side (b) is 4 feet (the distance of the ladder’s base from the tree).
- The hypotenuse (c) is the length of the ladder we are trying to find.
Substitute the given values:
3 2 + 4 2 = c 2 25 = c 2 To find the value of c, take the square root of 25: c = 5 So, the ladder needs to be 5 feet long to reach the treehouse! [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]History of Pythagorean Theorem
The Pythagorean Theorem, also known as the Baudhayana Theorem, is a mathematical rule that states that in a right triangle, the square of the hypotenuse (longest side) equals the sum of the squares of the other two sides. While it is named after Pythagoras of Samos (570–495 B.C.) for his first recorded proof, the theorem was known much earlier in cultures like Babylon, Egypt, India, and China. In India, it was referenced in the Baudhayana Shulba Sutra, centuries before Pythagoras, where it was applied to geometry and construction. Pythagoras is said to have discovered the theorem while observing square tiles, noticing that the areas of the squares on the shorter sides added up to the area of the square on the hypotenuse. The Egyptians used a "3-4-5" knotted rope to create right triangles for building, while Euclid, another great Greek mathematician, developed a geometric proof of the theorem in his famous book Elements . Even James A. Garfield, a U.S. President, contributed with his own proof using the area of a trapezoid. This theorem, with its deep history and many applications, continues to be one of the most important concepts in mathematics.Proof of Pythagoras Theorem
Consider a right-angled triangle with sides A, B, and C, where AC is the hypotenuse (longest side), and AB and BC are the two shorter sides. Draw a perpendicular line from B to AC, dividing the triangle into two smaller triangles.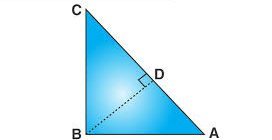
In △ABD and △ACB:
∠A is common to both triangles.
∠ADB =∠ABC = 90°.
Thus, △ABD ∼ △ACB (by AA similarity).
Similarly, △BDC ∼ △ACB.
From similarity:
AD/AB = AB/AC, which gives AB² = AD × AC ⇢ (1).
CD/BC = BC/AC, which gives BC² = CD × AC ⇢ (2).
Adding equations (1) and (2):
AB² + BC² = AC × AD + AC × CD
AB² + BC² = AC (AD + CD)
AB² + BC² = AC × AC
AB² + BC² = AC².
Since AC² = AB² + BC², the theorem is proved.
Converse of Pythagoras' Theorem Proof:
Statement: If the sides of a triangle are a, b, and c and a² + b² = c², then the triangle is considered a right triangle.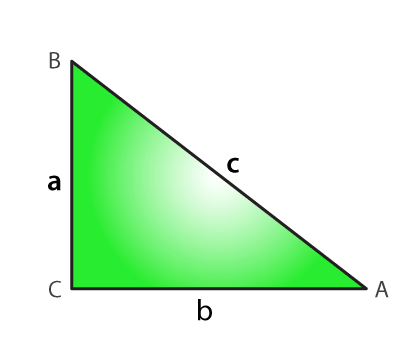
To prove this, construct another triangle △EGF,
where,
AC = EG = b and BC = FG = a.
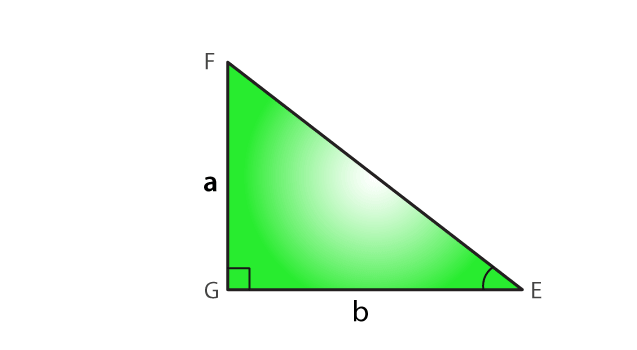Applying the Pythagoras Theorem to △EGF, we get EF² = EG² + FG² = b² + a².
In △ABC, applying the Pythagoras Theorem gives AB² = AC² + BC² = b² + a².
Comparing these results, EF² = AB², which implies EF = AB
By the SSS postulate, △ACB≅△EGF
Since ∠G in △EGF is a right angle, △ABC must also be a right triangle.
This proves the converse of the Pythagoras Theorem.
For a right triangle, the formula is a² + b² = c², where a, b, and c are the sides of the triangle.
Applications of the Pythagorean Theorem in Real Life
The Pythagorean Theorem is a foundational mathematical tool that helps solve practical problems by calculating distances and dimensions in right-angled triangles. It has widespread applications in everyday life and various professions. Here are different uses of the Pythagorean theorem in real life.- Construction and Building : It helps builders determine accurate dimensions for roofs, walls, and floors, ensuring structures are level and balanced.
- Navigation : Used by pilots and sailors to calculate direct routes between two points, saving time and fuel.
- Road Planning : Engineers use it to design diagonal shortcuts or calculate the distance between intersections.
- Home Improvement : People use it to measure ladder lengths or check if a rectangular object like a TV will fit diagonally into a space.
- Sports : Athletes and coaches use it to measure the shortest distance on fields or plan angles for plays.
- Robotics : Robots rely on it to calculate efficient paths when moving through spaces.
- Gardening and Design : Helps determine plot sizes or create straight edges in designs.
Pythagorean Theorem Solved Examples
Example 1: Find the hypotenuse where a = 3 cm and b = 8 cm. Solution: Label the sides : Hypotenuse (c): unknown. Shorter sides: a = 3 cm, b = 8 cm Write the formula : a 2 + b 2 = c 2 Substitute the values : 3 2 + 8 2 = c 2 Simplify : 9 + 64 = c Find c : c = √73≈8.54 cm Example 2: Determine if a triangle with sides a = 9 cm, b = 12 cm and c = 15 cm is a right-angled triangle . Solution : Label the sides : Hypotenuse (c) is the longest side: c = 15 cm Adjacent sides are a = 9 cm and b = 12 cm Use Pythagoras’ Theorem : a 2 + b 2 = c 2 Substitute the given values : 9 2 + 12 2 = 15 2 81 + 144 = 225 Simplify : 225 = 225 Since the equation holds true, the triangle satisfies Pythagoras’ Theorem, confirming it is a right-angled triangle. Example 3: Find the base of a right-angled triangle whose hypotenuse is 15 cm and whose height is 9 cm. Solution: Label the sides Here, a (perpendicular) = 9, c (hypotenuse) = 15, and we need to find b (base). Using Pythagorean Theorem : a 2 + b 2 = c 2Rearrange the formula to find b:
b= √c 2 −a 2 Substituting the values: b =√15 2 − 9 2 b = √225 − 81 b = √144 b = 12 cm Example 4: Find the perpendicular of a right-angled triangle whose hypotenuse is 17 cm and whose base is 8 cm. Answer : Label the sides Here, b (base) = 8, c (hypotenuse) = 17, and we need to find a (perpendicular). Using Pythagorean Theorem: a 2 + b 2 = c 2 Rearrange the formula to find the value of 'a': a = √c 2 − b 2Substituting the values:
a = √17 2 − 8 2 a = √289 − 64 a = √225 a = 15 cm| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Differentiation |
| Perimeter of Rectangle | Surface Area of Cylinder |
Pythagoras Theorem FAQs
What happens if one side of the triangle is zero?
If one side is zero, the triangle cannot exist as it collapses into a straight line. The Pythagorean Theorem requires three positive side lengths to form a valid right triangle.
Can the pythagorean theorem be applied to all triangles?
No, the pythagorean theorem specifically applies only to right-angled triangles. For other triangles, different rules, such as the law of cosines, are used to relate side lengths and angles.
Why is the hypotenuse always the longest side in a right triangle?
The hypotenuse is the side opposite the right angle, spanning the largest distance in the triangle. Mathematically, it is longer because its length equals the square root of the sum of the squares of the other two sides.
What are pythagorean triplets?
Pythagorean triples are sets of three positive integers (a, b, and c) that satisfy the Pythagoras theorem. In these triples, c represents the hypotenuse of a right-angled triangle, while aaa and bbb are its base and height. Such triples always form a right-angled triangle, known as a Pythagorean triangle.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.