Physics Wallah

Real Numbers: Meaning, Symbol, Properties, and Solved Examples

Real numbers are all numbers that represent continuous values, ranging from fractions to irrational numbers. Learn about Real Numbers in detail with solved examples here
authorImageChandni 23 Dec, 2024
Share

Share

Real Numbers

Real Numbers are used to measure continuous quantities like distance, time, and temperature. They include both rational and irrational numbers and can be represented as points on an infinite number line.

Each real number has a unique decimal expansion, which can go on forever. The real number system plays an important role in Mathematics, especially in calculus, where it helps define concepts such as limits, continuity, and derivatives.

The term “real” was introduced by René Descartes to distinguish these numbers from imaginary ones. In this blog, we will discuss real numbers in detail.

What are Real Numbers?

Real numbers are all the numbers that can be plotted on a number line. They include both rational and irrational numbers . Rational numbers can be expressed as fractions, such as 7, -3, 0.5, or 4/3, while irrational numbers cannot be expressed as exact fractions, like √2 and π. Real numbers cover whole numbers, integers, fractions, and decimals, representing a continuous and complete set of values. Some examples are 3, -1, 1/2, √2, π, and 2.5. So, what types of numbers are not real numbers?
  • Imaginary numbers , such as √−1 (the square root of -1), are not real numbers.
  • Infinity is also not a real number.
These special types of numbers are used in advanced mathematics but fall outside the category of real numbers. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/WhatsApp-Video-2024-12-18-at-17.55.24.mp4"][/video]

The Real N umber Line

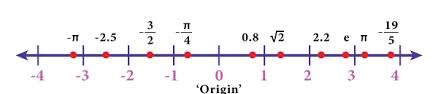
The real number line is a visual representation of all real numbers on a continuous, unbroken line. A specific point on this line is marked as the "origin" (0). Numbers to the right of the origin are positive, and numbers to the left are negative. A fixed distance is chosen to represent "1"; from there, whole numbers like 1, 2, 3, etc., are marked off to the right, while negative numbers like -1, -2, -3, etc. are marked to the left. Any point on this line represents a real number. These can include:
  • Whole Numbers: 5, 10, -3
  • Rational Numbers: 3/4, -2.5
  • Irrational Numbers: √3, π
However, you will not find numbers like infinity or imaginary numbers (such as √−1) on the real number line, as these do not belong to the set of real numbers.

Real Numbers Symbol

Real numbers are represented by the symbol R or ℝ. Here are symbols for other types of numbers:
  • Natural Numbers (N): 1, 2, 3,...
  • Whole Numbers (W): 0, 1, 2, 3,...
  • Integers (Z): -2, -1, 0, 1, 2,...
  • Rational Numbers (Q): Numbers that can be written as fractions, like 1/2 or -3/4
  • Irrational Numbers (Q’): Numbers that can't be written as fractions, like √2 or π

Properties of Real Numbers

Real numbers follow a set of basic rules for addition and multiplication . These rules help make calculations easier. Here’s a simple explanation of each property with examples.

Commutative Property

The order of the numbers doesn't matter. For Addition: a+b=b+a Example : 3+5=5+3 (Both equal 8) For Multiplication: a×b=b×a Example: 4×2=2×4 (Both equal 8)

Associative Property

The grouping of numbers doesn’t matter. For Addition: (a+b)+c = a+(b+c) Example: (2+3)+4=2+(3+4) (Both equal 9) For Multiplication: (a×b)×c=a×(b×c) Example: (2×3)×4 = 2×(3×4) (Both equal 24)

Distributive Property

You can distribute multiplication over addition. Rule a×(b+c) = a × b + a × c Example : 3×(4+2)=3 × 4 + 3 × 2 3 × 6 = 12 + 6 (Both equal 18)

Identity Property

Some numbers do not change their value when added or multiplied. For Addition (Additive Identity): a+ 0 = a Example: 7 + 0 = 7 For Multiplication (Multiplicative Identity): a × 1 = a Example: 5×1=5

Inverse Property

Combining a number with its inverse returns a neutral value . For Addition (Additive Inverse): a+(−a)= a + (-a) = 0 Example: 6+(−6)=0 For Multiplication (Multiplicative Inverse): a×(1/a)=1 (if a≠0) Example: 4×1/4=1

Real Numbers Solved Examples

Here are a few solved examples based on real numbers to help you better understand their application:

Example 1: Which of the following are real numbers?

333, −2.5-2.5−2.5,

Solution:
  • 333 is a whole number, which is a real number.
  • −2.5 is a decimal number, which is also a real number.
  • π is an irrational number, but it is still a real number.
Answer: 33 , −2.5-2.5 ,

Example 2: Find which of the variables a, b , c , and d represent rational numbers and which irrational numbers:

(i) a 2 =7 (ii) b 2 =16 (iii) c 2 =0.25 (iv) d 2 =20/9

Solution:

(i) a 2 = 7a On simplifying, we get: a = ± √7 Therefore, a is an irrational number

2. b 2 =16

On simplifying, we get: b = ± √4 Therefore, b is a rational number. 3 . c 2 = 0.25 On simplifying, we get: c=±0.5

Therefore, c is a rational number.

4. d 2 = 20/9 On simplifying, we get: d = ±20/3 Since √20 is irrational,

is an irrational number

Example 3: Place 7/4fraction on the number line.

Solution: 7/4=1.75 This lies between 1 and 2 on the number line. Answer: 7/4 is located between 1 and 2.

Example 4: Simplify 12√7/4√7

Solution: 12√7/4√7 12/4 × √7/√7 = 3 Example 5: What are the first 10 real numbers? Solution: Real numbers include all numbers on the number line, such as integers, fractions, decimals, and irrational numbers. However, if we focus on the first 10 real numbers, considering integers, they are: −5,−4,−3,−2,−1, 0, 1, 2, 3, 4
Real numbers form the backbone of mathematics, allowing us to measure, calculate, and solve real-world problems. Understanding real numbers helps unlock concepts like limits, continuity, and calculus. They are essential for both practical applications and advanced mathematical theories.
Related Articles
Subtraction Sums Word Problems
What is an Abacus? Math Puzzles
Multiplication Worksheets : Multiplication Sums

Real Numbers FAQs

Why are Irrational Numbers considered Real Numbers?

Irrational numbers, like π and √2, can still be represented on the number line even though they can’t be written as exact fractions.

How are real numbers used in real-life applications?

They are used in measuring lengths, temperatures, financial calculations, and scientific measurements.

What happens when you divide a Real Number by zero?

Division by zero is undefined in the real number system.

How do Real Numbers differ from Complex Numbers?

Real numbers do not include imaginary components, while complex numbers have both real and imaginary parts (e.g., 2+3i).

Is zero considered a positive or negative Real Number?

Zero is neither positive nor negative; it is a neutral real number.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.