Compound Interest: Definition, Formula, Example, How to Calculate
Khushboo Goyal28 Jul, 2025
Share
What is Compound Interest: Compound Interest is an important mathematical concept that shows how money can grow over time. Unlike simple interest, which is calculated only on the original amount, compound interest is calculated on both the initial amount and the already added interest.
This means the interest keeps building on itself, leading to faster growth as time passes. The longer the money is invested or saved, the more compound interest it will earn.
Compound interest is used in many areas of math, especially when studying exponential growth. Understanding compound interest helps students see how numbers can grow quickly when interest is added repeatedly over time, and it is a key concept in algebra and calculus. The definition of compound interest, formula, and method for calculating compound interest are given in the notes below.
What is Compound Interest?
Compound interest is the interest calculated on the principal amount and the interest that has already been added in previous periods. It differs from simple interest, where interest is calculated only on the original principal and not the accumulated interest.
Compound interest is calculated at regular intervals such as annually (once a year), semi-annually (twice a year), quarterly (four times a year), or monthly (twelve times a year). The more often the interest is added, the larger the final amount.
This means that compound interest helps the money grow faster than simple interest, as the interest keeps adding to the original amount and the interest earned so far.
Also Read: AM and PM
Compound Interest Formula
How to calculate Compound Interest: Compound interest is an important concept in mathematics where interest is calculated not only on the initial principal but also on the already added interest. This results in the money growing faster over time, as the interest keeps adding to the original amount and the previously earned interest.
The Compound Interest Formula:
CI Formula Compound Interest Formula) = A - P
The formula to calculate the amount (A) accumulated after a certain time period with compound interest is:
Where:
- A : Amount accumulated after the given period
- P : Principal amount (initial investment)
- r : Annual interest rate (written as a decimal)
- n : Number of times the interest is compounded per year
- t : Time period in years
Breaking Down the Formula
- (1 + r/n) : This part shows the interest rate for each compounding period. The annual interest rate (r) is divided by the number of times interest is added per year (n).
- (nt) : This represents the total number of compounding periods. It's found by multiplying the number of compounding periods per year (n) by the number of years (t).
- P(1 + r/n)^(nt) : This final part gives the total amount (A) after the specified time, showing how the principal (P) grows with compound interest.
Compound Interest Questions
Practicing compound interest questions goes a long way toward cementing the understanding. For example:
-
What is the amount received at the end if ₹5,000 were invested at 6% compound interest per annum for 5 years?
-
What would be the effect of the frequency of compounding on the total interest?
Compound Interest Formula Derivation
Compound interest formula is derived by calculating interest on both the principal and the accumulated interest over multiple periods. The following are step-by-step derivation of the Compound Interest Formula:
1. Principal and Interest for One Compounding Period:
Let P be the principal amount and r the annual interest rate. The interest earned after one compounding period is calculated by multiplying P by r/n , where n is the number of compounding periods per year. 2. Amount After One Compounding Period: After one compounding period, the total amount A will be the principal plus the interest earned:A = P(1 + r/n)
3. Amount After Two Compounding Periods:
After the second compounding period, interest is earned on the new amount P(1 + r/n) . The new total amount becomes:A = P(1 + r/n)(1 + r/n) = P(1 + r/n)²
4. Generalizing for t Years: For t years, with n compounding periods per year, the total number of compounding periods is n × t . The formula becomes:
This compound interest formula gives the future value A of an investment P after t years, considering the interest rate r , compounded n times per year.
CI Formula (Formula for Compound Interest) = A - P
Compound Interest Examples
Alice, a young entrepreneur, invests ₹10,000 in a promising tech startup that offers an annual interest rate of 8%, compounded quarterly. Let's calculate her earnings after 3 years.
- Principal (P) = ₹10,000
- Annual Interest Rate (R) = 8% = 0.08
- Number of Compounding Periods per Year (n) = 4 (quarterly)
- Time Period (t) = 3 years
Compound Interest Formula:
Formula for Compound Interest (CI) = A - P
Where, A is
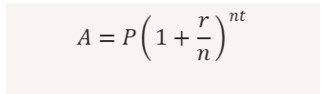
Step 1: Substitute the values into the formula:
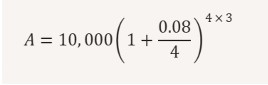
Step 2: Simplify inside the parentheses:
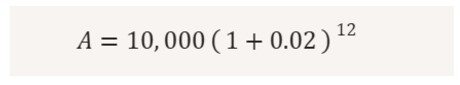
Step 3: Further simplify:
Step 4: Calculate the power:
Step 5: Multiply by the principal:
A ≈ 10,000 × 1.26824
Step 5: Multiply by the principal:
A ≈ 10,000 × 1.26824
Step 6: Final Amount:
A ≈ ₹12,682.42
Compound Interest (CI) = A - P = ₹12,682.42 - ₹10,000 = ₹2,682.42
After 3 years, Alice's investment grows to ₹12,682.42, earning her ₹2,682.42 as compound interest.
Also Check: Geometry
How to Calculate Compound Interest?
Eager to learn how to calculate compound interest, follow these steps:
- Determine the Principal Amount (P): Identify the initial amount of money that is being invested or borrowed. This is the starting point for the calculation.
- Convert the Interest Rate (r): If the interest rate is given as a percentage, convert it to decimal form. For example, 8% becomes 0.08. This makes it easier to work with in the formula.
- Identify the Compounding Frequency (n): Determine how often the interest is compounded in a year. It could be annually (once a year), semi-annually (twice a year), quarterly (four times a year), or monthly (12 times a year), etc.
- Calculate the Total Number of Compounding Periods (n × t): Multiply the number of compounding periods per year ( n ) by the total number of years ( t ) to get the total number of compounding periods.
- Apply the Compound Interest Formula: Substitute the values of P , r , n , and t into the compound interest formula to find the future value ( A ).
- Solve for the Future Value (A): Perform the necessary arithmetic operations to calculate the future value of the investment or loan. The result will give you the total amount after interest is added.
By following these steps, you can accurately calculate compound interest for any investment or loan.
Difference Between Simple and Compound Interest
Interest is the money paid for borrowing or the return earned on investments. There are two main types of interest: Simple Interest and Compound Interest . The following table provides between the two:
| Difference Between Simple and Compound Interest | ||
| Feature | Simple Interest (SI) | Compound Interest (CI) |
| Definition | Interest is calculated only on the initial amount of money (principal) throughout the investment period. | Interest is calculated on both the initial amount of money (principal) and the interest that has been added over time. |
| Formula | SI = (P × R × T) / 100 | Formula for Compound Interest (CI) = A - P |
| Where: | ||
| P | Principal amount | Principal amount |
| R | Rate of interest per period | Rate of interest per period |
| T | Time period (in years or months) | Time period (in years or months) |
| Interest Calculation | Interest is only calculated on the initial amount. | Interest is calculated on both the original amount and the interest added in previous periods. |
| Effect Over Time | The interest amount remains the same over time. | The interest amount grows over time due to compounding. |
| Growth of Investment | Investment grows at a steady, constant rate. | Investment grows at an increasing rate. |
| Time Factor Impact | Interest stays the same and does not change with time. | Interest grows faster as time passes because of compounding. |
| Frequency of Compounding | No compounding (interest is not added to the principal). | Interest is added to the principal at regular intervals (e.g., yearly, quarterly). |
| Use Cases | Often used for short-term loans or investments. | Commonly used for long-term savings or loans where growth over time matters. |
| Example | If you invest $1,000 at 5% yearly interest for 3 years, interest is always calculated on $1,000. | If you invest $1,000 at 5% yearly interest for 3 years, the interest will be calculated on the total amount each year, including previous interest. |
| Advantages | Easy to calculate and understand. | Results in higher returns over time due to compounding. |
| Disadvantages | Gives lower returns compared to compound interest. | More complex to calculate and track, especially for long periods. |
About CuriousJr Mental Maths Classes
At CuriousJr , part of Physics Wallah, we provide specialized Mental Maths Classes that help students master problem-solving skills. With over 50 mental math strategies our program is designed to enhance both speed and accuracy in calculations.
Our classes focus on developing logical reasoning and critical thinking skills enabling students to tackle complex problems effortlessly. By participating in our CuriousJr classes, you will not only improve your ability to solve challenging tasks but also strengthen your overall cognitive abilities. This empowers you to achieve more in less time making learning math an enjoyable and rewarding experience.
| Related Articles | |
| Pie Chart | Cube |
| AM and PM | Geometry |
| Mental Maths Worksheet | Vedic Maths |
Compound Interest FAQs
What means compound interest?
What is compound interest with example?
Is compound interest good or bad?
Can Compound Interest be Greater than Principal?
What Are the Units of Compound Interest?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
