
Trigonometric Table: Trigonometry is a core branch of mathematics focused on the relationships between the angles and sides of triangles. It primarily deals with right-angled triangles and key trigonometric functions such as sine, cosine, and tangent, which help define these relationships.
A widely used tool in trigonometry is the trigonometric table, which lists the values of these functions for commonly used angles. This table makes calculations easier and aids in solving problems involving angles, distances, and measurements.
Mastering how to read and use a trigonometric table can significantly improve your problem-solving skills in both theoretical and real-world scenarios.
In this blog, we’ll break down the concept of the trigonometric table and explain how it can be used effectively. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]What is a Trigonometric Table?
A trigonometric table is a reference chart that provides the values of the six primary trigonometric functions: sine (sin), cosine (cos), tangent (tan), cosecant (CSC), secant (sec), and cotangent (cot).
The table typically covers standard angles such as 0°, 30°, 45°, 60°, and 90°, but it can also include extended angles like 180°, 270°, and 360°. The values in the trigonometric table simplify calculations in various mathematical and real-world applications, especially in fields like geometry, physics, engineering, astronomy, and computer graphics.
Six Important Trigonometric Functions Formulas
The six trigonometric functions, also referred to as trigonometric ratios, are derived from specific formulas based on the sides of a right triangle.
To understand these functions, it's essential to know the three sides of a right triangle: the opposite side, the adjacent side, and the hypotenuse.
These relationships are fundamental to defining each trigonometric function. Below, we explain the meaning and formulas for each of the trigonometric ratios. If θ represents the angle in a right-angled triangle, then...
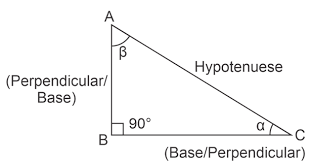
Sine (sin) : The sine of an angle is the ratio of the opposite side to the hypotenuse in a right-angled triangle.
sin(θ)=Opposite Side/ Hypotenuse
Cosine (cos) : The cosine of an angle is the ratio of the adjacent side to the hypotenuse.
cos(θ)=Adjacent Side/Hypotenuse
Tangent (tan) : The tangent of an angle is the ratio of the opposite side to the adjacent side . It can also be expressed as the ratio of sine to cosine.
tan(θ)=Opposite Side/Adjacent Side
Cosecant (csc) : The cosecant of an angle is the reciprocal of sine. It represents the ratio of the hypotenuse to the opposite side.
csc(θ) = 1 / sin(θ) = Hypotenuse / Opposite Side
Secant (sec) : The secant of an angle is the reciprocal of cosine. It represents the ratio of the hypotenuse to the adjacent side.
sec(θ) = 1 / cos(θ) = Hypotenuse / Adjacent Side
Cotangent (cot) : The cotangent of an angle is the reciprocal of a tangent . It represents the ratio of the adjacent side to the opposite side .
cot(θ) = 1 / tan(θ) = Adjacent Side / Opposite Side
[video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]The Trigonometric Table for Standard Angles
The table below shows the values of trigonometric functions for standard angles:
Trigonometric Table |
|||||||
| Angle in degrees (θ) | Angle (in radians) | sin(θ) | cos(θ) | tan(θ) | csc(θ) | sec(θ) | cot(θ) |
| 0° | 0 | 0 | 1 | 0 | ∞ | 1 | ∞ |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 | 2 | 2/√3 | √3 |
| 45° | π/4 | 1/√2 | 1/√2 | 1 | √2 | √2 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 | 2/√3 | 2 | 1/√3 |
| 90° | π/2 | 1 | 0 | ∞ | 1 | ∞ | 0 |
How to Read and Understand the Trigonometric Table?
The trigonometric table is a valuable tool for understanding the values of different trigonometric functions for standard angles. Here’s a clear breakdown of each function and how their values change across these angles.Sine (sin)
Sine values range from 0 to 1 , starting from 0° (where sin(0°) = 0) and increasing to 1 at 90°.Examples:
sin(30°) = 1/2 (This means the sine of 30° is 0.5)
sin(45°) = 1/√2 ≈ 0.707 (This is the sine of 45°, which is approximately 0.707)
Cosine (cos)
Cosine values start at 1 at 0° and decrease to 0 at 90°.Examples:
cos(30°) = √3/2 ≈ 0.866 (This is the cosine of 30°, which is approximately 0.866)
cos(60°) = 1/2 (This means the cosine of 60° is 0.5)
Tangent (tan)
Tangent is undefined at 90° because cos(90°) = 0 .Examples:
tan(45°) = 1 (This is because sin(45°) = cos(45°), so their ratio is 1)
tan(60°) = √3 ≈ 1.732 (This means the tangent of 60° is approximately 1.732)
For cosecant (csc), secant (sec), and cotangent (cot)
These are simply the reciprocals of ratios such as sine, cosine, and tangent. To find these, simply flip the values.Example:
- csc(30°) = 1 / sin(30°) = 1 / 0.5 = 2
- sec(30°) = 1 / cos(30°) = 1 / 0.866 ≈ 1.154
- cot(30°) = 1 / tan(30°) = 1 / 0.577 ≈ 1.732
How to Memorize the Trigonometric Table?
Here are the tips to memorise the trigonometric table using a one-hand tick: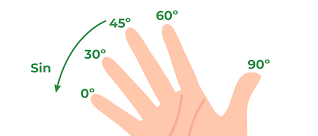
For S ine (sin)
Count the number of fingers on the left side of each finger for the angle. Divide that number by 4. Then, take the square root of the result. Example: For 30° , the left side has 1 finger (the pinky). Divide 1 by 4: 1 ÷ 4 = 0.25 Take the square root of 0.25 : √0.25 = 0.5 So, sin(30°) = 0.5 .For C osine (cos)
Cosine values are the same as sine values but in reverse order. Starting with the thumb (90°) and going backward. Example: For 30° , the cosine value is the same as sin(60°) . From the trick, we know that sin(60°) = 0.866 . So, cos(30°) = 0.866 . Count the number of fingers on the left side of each finger for the angle.For T angent (tan):
Tangent is the ratio of sine to cosine. So, you can use the sine and cosine values you already have to find the tangent value. Example: For 30° , we already know:- sin(30°) = 0.5
- cos(30°) = 0.866
- Now, calculate tan(30°) :
For C osecant (csc), S ecant (sec), and C otangent (cot)
These are just the reciprocals of sine, cosine, and tangent. To find these, simply flip the values. Example:- csc(30°) = 1 / sin(30°) = 1 / 0.5 = 2
- sec(30°) = 1 / cos(30°) = 1 / 0.866 ≈ 1.154
- cot(30°) = 1 / tan(30°) = 1 / 0.577 ≈ 1.732
Applications of the Trigonometric Table
T he trigonometric table is widely used in various fields, including:- Geometry : Calculating unknown sides or angles in triangles.
- Physics : Solving problems related to waves, oscillations, and forces.
- Engineering : Designing structures and analyzing mechanical systems.
- Astronomy : Determining distances between celestial bodies.
- Navigation : Calculating direction and distances in GPS and map systems.
The trigonometric table is an essential tool for solving problems involving angles and triangles. By understanding and memorizing the values of trigonometric functions for standard angles, you can quickly and accurately perform calculations in mathematics, physics, engineering, and more.
Mastering the trigonometric table not only simplifies problem-solving but also deepens your understanding of the relationships between angles and sides in triangles. Whether you’re a student, educator, or professional, having a firm grasp of the trigonometric table can give you an edge in solving real-world challenges.
| Related Articles | |
| Perimeter of a Triangle | Isosceles Triangle |
| Celsius to Fahrenheit | Natural Numbers |
| Surface Area of Cylinder | |
Trigonometric Table FAQs
Why are Trigonometric Tables used?
How accurate are the values in a Trigonometric Table?
How can I use a Trigonometric Table for solving real-life problems?
How do I find the cotangent of an angle from the Trigonometric Table?
What is the difference between a Trigonometric Table and a unit circle?
How do I read a trigonometric table?









