Unit Fraction- Definition, Examples, Practice Problems

Unit Fraction: Did you get confused when you heard the term Unit Fraction for the first time? If yes, then you're not alone. Many students feel the same. A unit fraction is a fraction where the numerator is always 1 but the denominator can be any whole number greater than 1. It shows one equal part of something that is divided into many parts.

Learning about unit fractions can help you understand the basics of dividing things into equal parts. To know more about what unit fraction is with examples and how it is used in solving problems, keep reading.

Read More: Natural Numbers

What is Unit Fraction? An Overview

In Mathematics, fractions are used to show parts of something whole. For example, if you cut a chocolate bar into 4 equal pieces and eat 1 piece, you ate 1 out of 4 pieces, which is written as 1/4.

Among different types of fractions, Unit Fraction is a special type of fraction. It always has 1 at the top, which is called the numerator and any number at the bottom, which is called the denominator. It shows just one part of something that is equally divided. For example:

• 1/2 means one out of two equal parts.

• 1/3 means one out of three equal parts.

• 1/5 means one out of five equal parts.

Enroll Now for Kids Online Classes

Unit Fraction Definition

In those kinds of fractions where the numerator is always 1 and the denominator can be any positive integer are defined as Unit Fraction. These fractions represent just one section of a whole that has been divided into equal sections. Since the numerator is 1, it shows that we are looking at one part out of the total number of equal parts. The word "unit" means one, which is why these are called unit fractions.

What is Denominator and Numerator?

While learning about unit fractions, we will be using terms like Numerator and Denominator many times. Therefore, knowing what denominator and numerator mean in a fraction is important to understand this topic in a better way.

• Numerator is the top number of a fraction that tells us how many parts we have. For example: In the fraction 3/5, 3 is the numerator, so we have 3 parts.

• Denominator is the bottom number of a fraction that tells about how many equal parts the whole is divided into. For example: In the fraction 3/5, 5 is the denominator, so the whole is divided into 5 equal parts.

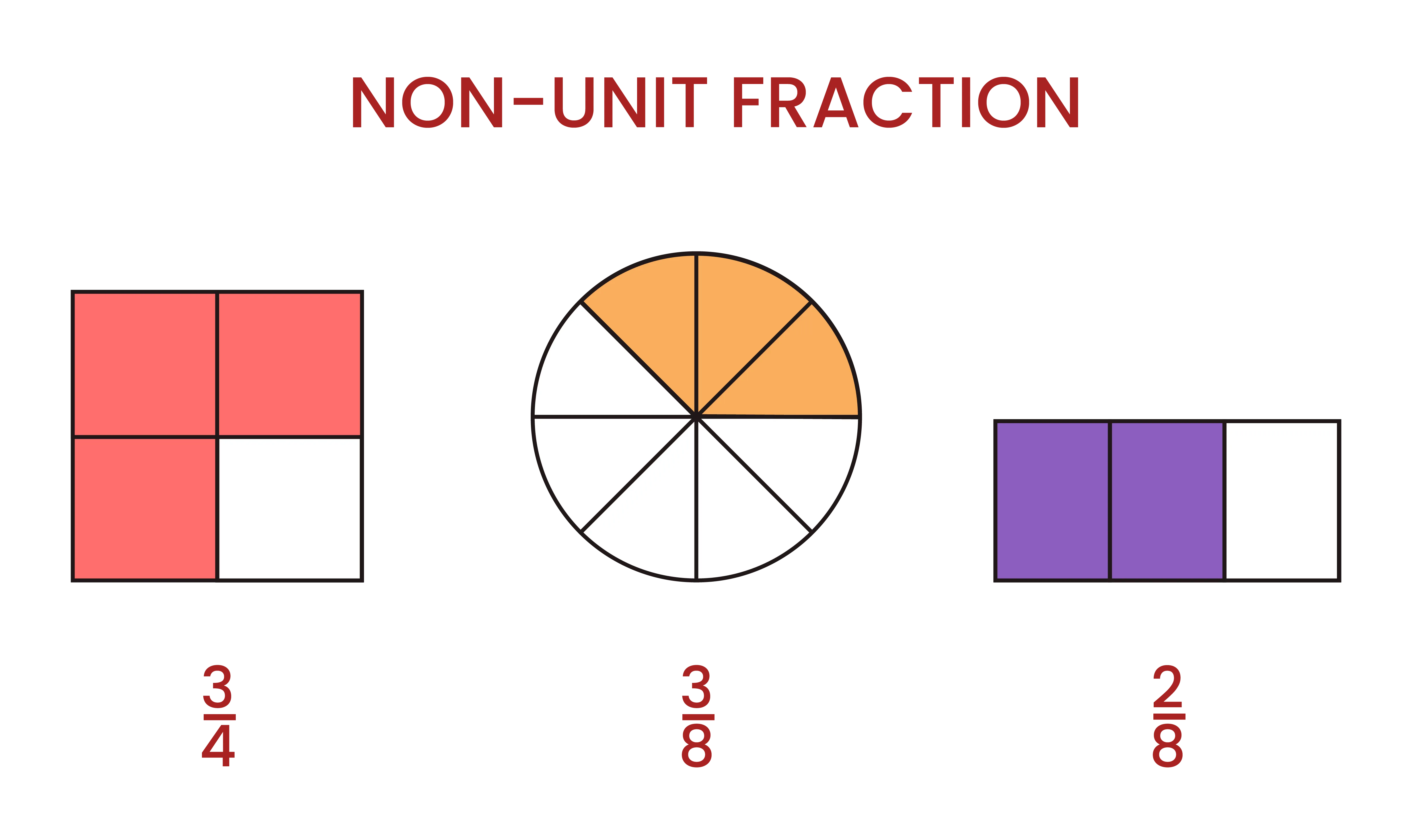
What is the Difference Between Unit and Non-Unit Fractions?

In math, a unit fraction is a fraction where the numerator is always 1 but the denominator can be any whole number, but it has to be bigger than 0. A unit fraction shows one part of something that is divided into equal parts, like 1/3 (one third), 1/4 (one fourth), etc.

On the other hand, a non-unit fraction has a numerator that is more than 1. The denominator can still be any whole number greater than 0. Non-unit fractions show more than one part of something divided into equal parts. For example: 2/3 (two-thirds), 3/4 (three-fourths), 5/6 (five-sixths), etc.

Key Properties of Unit Fractions

Unit fractions have some important properties that can help you in understanding how they work. Find out the key properties of Unit Fractions here:

• Numerator is Always 1: The numerator of a unit fraction is always 1, and the denominator can be any positive whole number greater than 1

• Multiplication with Whole Numbers: When a unit fraction is multiplied by a whole number, the answer may not come in another unit fraction. But dividing a unit fraction by a whole number can sometimes give an answer in a unit fraction. For example: 1/8 × 5 = 5/8 (Not a unit fraction) | 1/12 × 6 = 6/12 = 1/2 (Unit fraction)

• Multiplying Two Unit Fractions: When two unit fractions are multiplied together, the answer will always be another unit fraction. For example: 1/5 × 1/5 = 1/25 | 1/9 × 1/9 = 1/81.

• Dividing Unit Fractions by Rational Numbers: When dividing unit fractions by other rational numbers, the answer will not be a unit fraction.

Read More: Geometry

How to Multiply Unit Fractions with Unit Fractions?

To multiply two unit fractions, just multiply the top numbers (numerators) together and the bottom numbers (denominators) together. For example: Multiply 1/2 × 1/3.

• First, multiply the numerators: 1 × 1 = 1.

• Then multiply the denominators: 2 × 3 = 6.

So, the answer is: 1/2 × 1/3 = 1/6.

Multiplying Unit Fractions with Non Unit Fractions

When multiplying a unit fraction with a non-unit fraction, we will still multiply the numerators together and the denominators together. For example: Multiply 1/2 × 3/4.

• First, start by multiplying the numerators: 1 × 3 = 3.

• Then, multiply the denominators: 2 × 4 = 8

• Finally, 1/2 × 3/4 = 3/8.

How to Add Unit Fractions With the Same and Different Denominators?

Now that you've learned how to multiply unit fractions with non-unit fractions, let’s understand how you add unit fractions having the same denominator or different denominators.

Adding Unit Fractions With the Same Denominators

When the denominators are the same, we can just add the numerators and keep the denominator the same. After adding, we simplify if needed. For example: Add 1/4 and 1/4:

• Here the denominators are the same (4) so we can add the numerators: 1 + 1 = 2. We will keep the denominator as it is. So, the solution will be 1/4 + 1/4 = 2/4, which simplifies to 1/2.

So, the answer to 1/4 + 1/4 = 1/2.

Adding Unit Fractions With Different Denominators

In questions where the denominators of unit fractions are not similar, we need to find a common denominator first. Here's how we can do it:

Step 1: Find the Least Common Denominator (LCD). The LCD is the smallest number that both denominators can divide into. 

• For example: Add 1/3 and 1/6.

• Solution: The multiples of 3 are: 3, 6, 9, 12, 15, 18, etc and the multiples of 6 are: 6, 12, 18, etc. Therefore, the LCD here is 6.

Step 2: Convert each fraction to have the LCD (6) as the denominator.

• To make 1/3 have a denominator of 6, we multiply both the numerator and denominator by 2: 1/3 × 2/2 = 2/6

• 1/6 already has the denominator 6, so we will keep it the same: 1/6.

Step 3: Now that the denominators are the same, start with adding the unit fractions.

• First, we add the numerators: 2 + 1 = 3

• So, the answer is going to be: 2/6 + 1/6 = 3/6, which simplifies to 1/2.

Subtracting Unit Fractions With Different Denominators

Subtracting unit fractions is similar to how we add them; the only change here is instead of adding the numerators, we subtract them. Check the example below to understand it clearly:

Example: Subtract 1/2 from 3/4:

Step 1: Find the LCM of 2 and 4.

• The multiples of 2 are 2, 4, 6, 8, ...

• The multiples of 4 are 4, 8, 12, and so on. So the LCM we need here is 4.

Step 2: Convert each fraction to have the LCM 4 as the denominator.

• 1/2 becomes 2/4 after multiplying both the numerator and denominator by 2.

• 3/4 is going to be the same as 3/4 because it already has 4 as the denominator.

Step 3: Now subtract the unit fractions.

• Subtract the numerators: 3 - 2 = 1

• The denominator stays the same: 4. So, the answer is going to be: 3/4 - 2/4 = 1/4.

And that’s how you can add or subtract unit fractions. The important step here is to find a common denominator and then either add or subtract the numerators.

What is Unit Fraction With Example?

By now, you must have understood the definition of a unit fraction. Let’s now understand it better with a few sets of examples:

Example 1:

Question: A watermelon is cut into 6 equal slices. If one person eats 1 slice, what fraction of the watermelon did they eat?

Answer: They ate 1/6 of the watermelon.

Example 2: 

Question: A notebook has 10 equal sections. If 1 section is used for English, how can we show the English section as a fraction?

Answer: The English section is 1/10 of the whole notebook. This is a unit fraction.

Example 3 (Adding Unit Fractions):

Question: Add 1/6 and 1/6.

Answer: To add unit fractions, we add the numerators and keep the denominator the same like: 1/6 + 1/6 = 2/12 = 1/6.

Example 4 (Multiplying Unit Fractions):

Question: Multiply 1/5 and 1/5.

Answer: When multiplying unit fractions, you need to multiply the numerators and denominators like this: 1/5 × 1/5 = 1/25.

Example 5 (Dividing by a Whole Number):

Question: Divide 1/6 by 3.

Answer: To divide by a whole number, multiply the denominator by the whole number, like this: 1/6 ÷ 3 = 1/(6 × 3) = 1/18.

Read More: Angles

Unit Fractions Practice Problems With Solutions

Unit fractions are an important part of learning fractions. Practicing them helps you understand how to add, subtract, and divide fractions. Here are some practice problems with solutions to help you get better at using unit fractions in different situations:

1. Problem:  In the list of fractions given below, identify the unit fractions.
1/3, 5/7, 1/5, 2/8, 1/9, 3/4, 1/6

Answer: The unit fractions are 1/3, 1/5, 1/9, and 1/6.

2. Problem: Add the following unit fractions:
1/6 + 1/8

Solution: To add fractions, first you need to find the least common denominator (LCD), which is 24 in this case.
So,
1/6 = 4/24
1/8 = 3/24
Now, adding them:
4/24 + 3/24 = 7/24

Answer: The sum is 7/24.

3. Problem: Subtract the following unit fractions:
1/4 - 1/10

Solution: Find the least common denominator, which is 20.
1/4 = 5/20
1/10 = 2/20
Now, subtracting them:
5/20 - 2/20 = 3/20

Answer: The result is 3/20.

4. Problem: Divide the following unit fraction by a whole number:
1/12 ÷ 5

Solution: To divide a fraction by a whole number, multiply the denominator of the fraction by the whole number.
1/12 ÷ 5 = 1/(12 × 5) = 1/60

Answer: The result is 1/60.

Unit Fractions Practice Problems With Solutions

Unit fractions are an important part of learning fractions. Practicing them helps you understand how to add, subtract, and divide fractions. Here are some practice problems with solutions to help you get better at using unit fractions in different situations:

Want to make math easier and faster for your child? CuriousJr Online Classes for Kids helps students from Class 1 to 8 learn smart tricks to solve problems quickly and think more clearly. With engaging lessons and creative practice, your child will start enjoying maths while building strong problem-solving skills. Enroll now and help your child become confident in Mathematics!