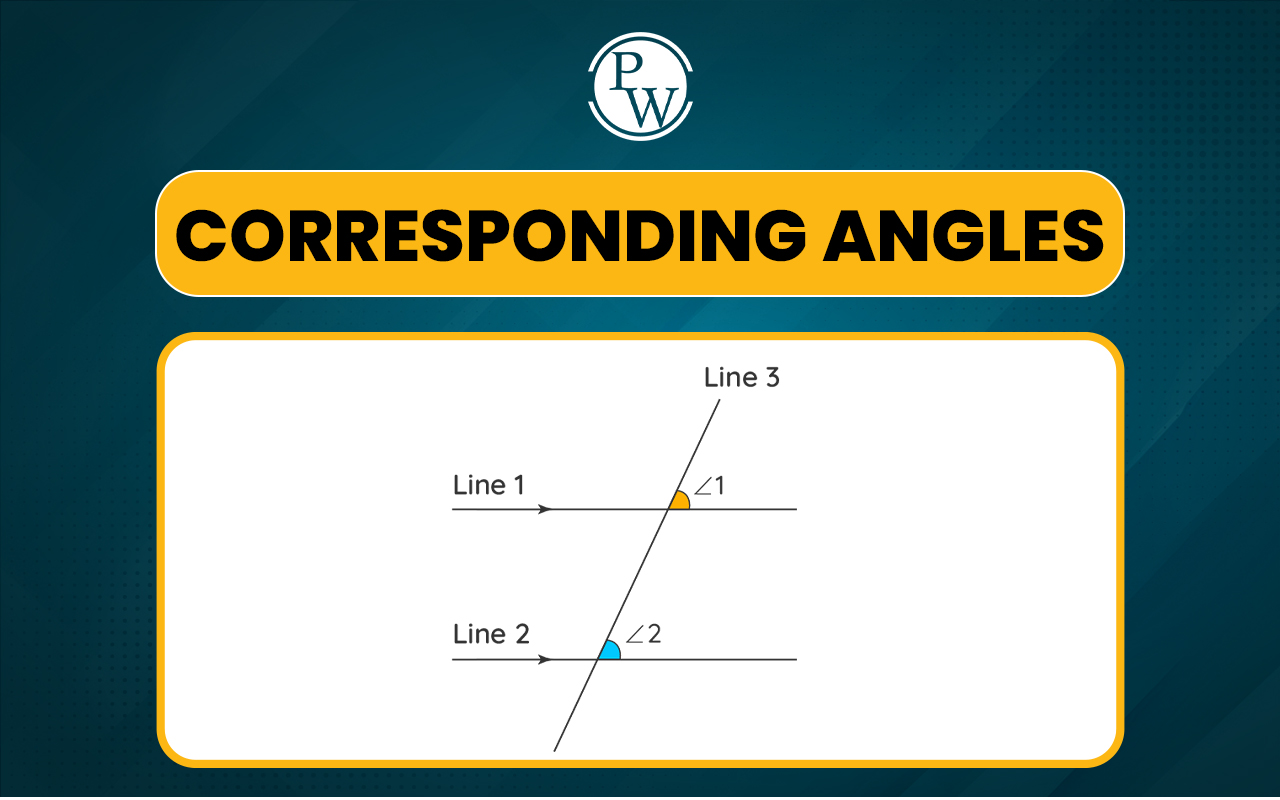
Corresponding Angles: Definition, Theorem, and Solved Examples
Corresponding angles are equal angles formed when a transversal crosses parallel lines. Understand the corresponding angles theorem and its real-life applications here.
Chandni 16 Jan, 2025
Share
Corresponding Angles are an important fundamental concept in geometry that tells us the nature and relationship between angles when transversal lines intersect parallel lines.
As a math enthusiast or looking to apply this knowledge in real-world scenarios, understanding corresponding angles can enhance your knowledge of theoretical concepts and practical applications. In this article, get useful insights into the concept of corresponding angles with detailed explanations and examples. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]What are Corresponding Angles?
When two or more lines on the same plane are crossed by another line (called a transversal), the angles formed on the same side of the transversal are called corresponding angles. There can be two different instances of forming corresponding angles as follows: Angles formed by the intersection of non-parallel lines and a transversal In the figure given below, Line 1 and Line 2, which are not parallel to each other, are intersected by another Line 3, and the angles 1 and 2 formed are known as corresponding angles.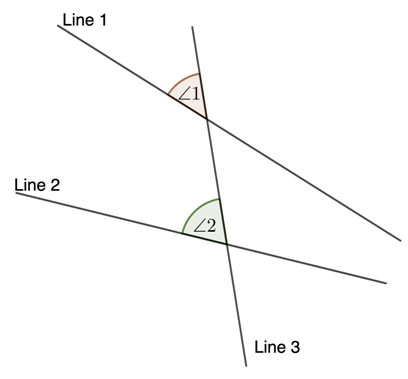
Angles formed by the intersection of parallel lines with a transversal
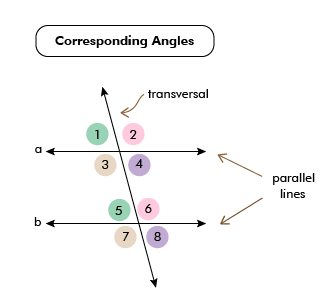
Interior and Exterior Angles
It is observed that there are always a pair of corresponding angles formed. Out of these two angles, one is called the interior angle, and the other is called the exterior angle.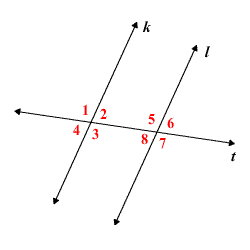
In the above image, out of two corresponding angles ∠1 and ∠5, angle ∠1 is called the exterior angle because it is formed outside the parallel lines, and angle ∠5 is called the
interior angle
because it is formed between the two parallel lines (
k
and
l
)
Corresponding Angles Characteristics
There are particular characteristics or properties for the angles created when a transversal crosses parallel lines. If two lines are parallel and a transversal line intersects them, then the measurement of corresponding angles formed on either side of the transversal are equal.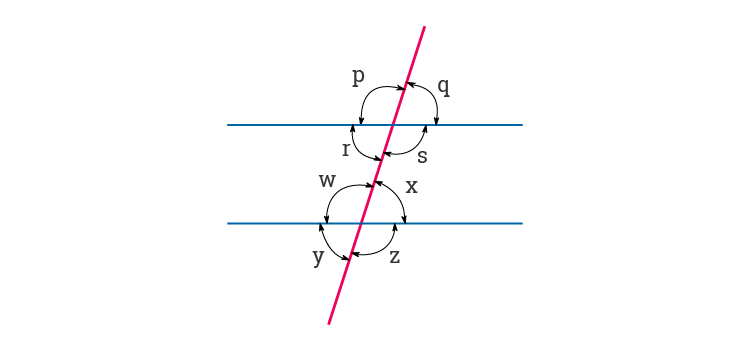
In the above figure, the two parallel lines are cut by a transversal. As a result, eight angles are formed between the lines and the transversal.
As per the theorem of corresponding angles, the angles formed by the first line with transversal and the corresponding angles formed by the second line with transversal are equal in measurement.
Therefore, we can say,
Angle ∠p = ∠w
Angle ∠q= ∠x
Angle ∠r = ∠y
Angle ∠s = ∠z
[video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]
The Converse Theorem
The converse of the statement is also true. It means if a transversal intersects two lines in such a way that the corresponding angles formed are equal or congruent, then it can be said that the two lines are parallel to each other.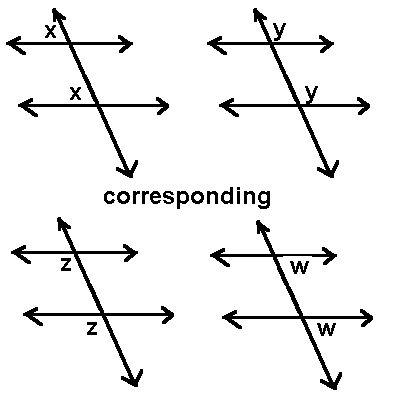
In the above image, we have found that four pairs of corresponding angles are formed between the transversal and two given lines, and each angle of the pair is equal in measurement. Therefore, we can say that the lines are parallel.
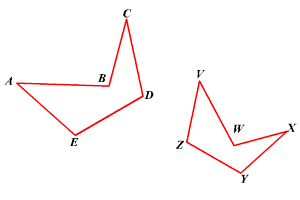
Corresponding Angles of Polygons
Two polygons are considered similar if they have the same shape but may differ in size. When two polygons are similar:- Their corresponding angles are congruent (equal in measure).
- Their corresponding sides are proportional in length.
Example: Corresponding Angles in Similar Triangles
Let's examine the two similar triangles in the given image: △ XYZ and △ PQR .- ∠X = ∠P
- ∠Y = ∠Q
- ∠Z = ∠R
Here,
the corresponding angles are equal, which means:
Angle ∠A = ∠V
Angle ∠B= ∠W
Angle ∠C = ∠X
Angle ∠D = ∠Y
Angle ∠E = ∠Z
Application of Corresponding Angles
Corresponding angles make many everyday tasks easier and more accurate. Here are a few real-life applications of corresponding angles:- Building Bridges and Roads : Corresponding angles help make bridges and roads straight and safe by keeping parts in the right position.
- Designing Buildings : Architects use these angles to design walls, windows, and roofs to be perfectly aligned.
- Making Patterns : Artists use corresponding angles to create beautiful and even patterns in their work.
- Sports and Games : In sports like golf or archery, these angles help players aim better by measuring heights and slopes.
- Machines and Gears : Engineers use them to make sure parts of machines and gears fit together and work smoothly.
- Navigation : Pilots and sailors use corresponding angles to figure out directions and distances.
Corresponding Angles Solved Example
1. In the image given below, find the value of x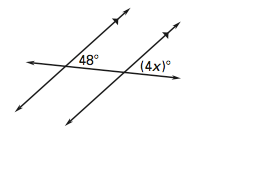
Solution:
Applying the theorem of corresponding angles, we can write: 4X = 48 Or, x = 48/4 = 12 Ans. The value of x is 12. 2. In the figure given below, find the value of x and y.
Solution:
Lines AB and CD are parallel and are intersected by a transversal. As per the properties of corresponding angles, we can write: x = 130 Again, using the corresponding angle and complementary angle theorem, we can say, y + 50 = 180 Or, y = 150 - 80 = 130| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Differentiation |
| Perimeter of Rectangle | Surface Area of Cylinder |
Corresponding Angles FAQs
If corresponding angles theorem apply when the lines crossed by the transversal line are not parallel?
The corresponding angles theorem doesn’t apply when the lines crossed by the transversal are not parallel.
What is the difference between corresponding angles and alternate angles?
The corresponding angles remain on the same side of the transversal while alternate angles are on the opposite side of the transversal.
What are parallel lines?
In geometry, parallel lines are those lines on the same plane that never meet or cross each other.
Mention a practical application of the corresponding angle.
The railway tracks are constructed parallelly by making the corresponding angles equal.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App