Less Than Symbol in Maths: Meaning, Tricks, and Examples
The less than symbol in Maths is used to show that one value is smaller than another. Learn an easy trick to remember the less than symbol with solved examples here.
Chandni 23 Jan, 2025
Share
Less Than:
In math, we often compare numbers to see which one is bigger or smaller. The "Less Than
S
ymbol" (<) is like a friendly arrow that points to a smaller number. Think of it as a crocodile’s mouth that’s always hungry for the bigger number!
For example:
- 3 < 5: The crocodile opens its mouth toward 5 because it’s bigger than 3 .
- 7<10: The crocodile chooses 10 because it’s the larger snack!
[video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]
What is Less Than ?
T he concept of "less than" refers to comparing two values to determine which one is smaller. The symbol for "less than" is “<”, and it helps compare numbers, weights, heights, and other quantities. For example, in the expression 2 < 6, it means 2 is less than 6. This symbol is commonly used in mathematical equations and real-world comparisons. Here are a few other examples to understand its application:- 5 < 8: Five is smaller than eight.
- -10 < -3: Negative ten is less than negative three.
- 0 < 15: Zero is smaller than fifteen.
- 3y + 2 < 14: The value of 3y + 2 is less than 14. For y = 3, the expression becomes 9+2 =11, and 11 < 14, which is true.
Tricks to Remember the Less Than Symbol
The less than symbol (“<”) and its counterpart, the greater than symbol (“>”), have similar appearances but point in opposite directions. To avoid confusion between the two, you can use these two simple tricks to remember which symbol represents “less than”:
The L Method
The word “less” starts with the letter L , and the less than symbol (“<”) resembles a slanted version of the letter L . This can help you associate the symbol with "less than."The Smaller Mouth Method
Think of the less-than symbol (“<”) as an open mouth pointing toward the smaller value. The wider endpoints are to the larger value, and the narrow endpoints are to the smaller value. For example: 3 < 7 The open side of the symbol faces 7, the larger value, while the pointed end faces 3, the smaller value .Representing "Less Than" on a Number Line
The less than symbol (“<”) is represented on a number line to show the range of possible values for an inequality visually. Here’s how it’s done in a simple, step-by-step way:Steps to Represent x<3
Here. we a re discussing steps to represent x< 3 on a number line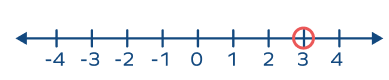
Step 1:
Identify the Limit Value
:
The inequality x<3 means x can take any value smaller than 3, but
not 3 itself
. On the number line, the number 3 is the
limit value
.
Step 2: Mark the limit value with an open circle:
Draw an open circle at 3. The open circle indicates that 3 is not included in the solution.
Step 3: Draw the Arrow for Smaller Values
:
Starting from the open circle at 3, draw an arrow extending to the
left
toward smaller numbers. This shows that all values less than 3 are part of the solution.
Note:
Here, the open circle represents that the limit value (in this case, 3) is
excluded
from the solution. This is because x<3 strictly means x is smaller than 3, not equal to 3.
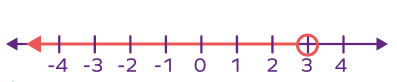
If the Inequality Is x ≤ 3x
For x ≤ 3x the steps are similar, but there is one key difference: Step 1: Use a Filled Circle : Instead of an open circle, draw a filled circle at 3. The filled circle means the limit value (3) is included in the solution. Step 2: Draw the Arrow to the Left : Extend the arrow to the left as before, covering all smaller values, including 3.Less Than, Greater Than, Equal To, and Not Equal To Symbols Comparison
The table below explains the mathematical symbols used to compare numbers, along with their names, meanings, and examples.| Symbol/Sign | Name | Indicates | Example | Explanation |
|---|---|---|---|---|
| < | Less than | The left value is smaller than the right value | 4 < 6 | 4 is less than 6 |
| - | Equal to | The left and right values are the same | 10 =10 | 10 is equal to 10 |
| ≠ | Not Equal To ≠ | The "not equal to" symbol is used to indicate that two values are not the same or do not hold equality. | 4 ≠ 7 | 4 is not equal to 7 |
| > | Greater than | The left value is larger than the right value | 12 > 8 | 12 is greater than 8 |
Less Than Symbol Solved Example
1: Solve for x in 5x < 25 .
Solution:
To find the value of x , divide both sides of the inequality by 5: 5x < 25 x < 25/ x < So, the solution is x<5x.Example 2: A library has two sections for books. The first section contains 120 books, and the second section contains 95 books. Which section has fewer books?
Solution:
To compare the number of books in both sections:- The first section has 120 books.
- The second section has 95 books.
Example 3: Ravi’s savings in May were at least ₹20 less than his savings in April. If Ravi saved ₹180 in May, determine his savings in April.
Solution:
The given statement is: "Ravi’s savings in May were at least ₹20 less than his savings in April. Let S represent Ravi’s savings in April. The inequality expression becomes: S− 20 ≥180 Add 20 to both sides of the inequality: S ≥ 200 Therefore, Ravi’s savings in April were at least ₹200.Less Than Symbol FAQs
What’s an example of "less than" in measurements?
A box weighing less than 10 kg" means its weight is x < 10.
How do you compare two values using <?
Check which value is smaller and place the smaller number on the left.
What does 𝑥 < 𝑦 mean in algebra?
It means the variable 𝑥 is smaller than the variable y.
How to write 45 is not greater than 50?
To express "45 is not greater than 50," you can write:
45 ≤ 50
This means 45 is less than or equal to 50, which shows 45 is not greater.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
