Area of Equilateral Triangle - Formulas, Derivation, Solved Examples
Area of Equilateral Triangle can be calculated using the formula (√3/4) × side². Learn how to find the area with examples and step-by-step guidance for better understanding.
Shruti Dutta8 Jan, 2025
Share
The area of equilateral triangle refers to the amount of space enclosed within its boundaries. An equilateral triangle is a unique type of triangle where all three sides are of equal length, and all three angles measure 60 degrees .
Due to its symmetry, calculating the area of an equilateral triangle is straightforward and can be done using a specific formula that depends on the length of one side. This formula simplifies the process, making it easier to find the area without needing to measure the height or other elements of the triangle directly. Understanding how to calculate the area of an equilateral triangle is essential in various fields, including geometry, engineering, and design.Area of Equilateral Triangle
The length of its sides determines the Area of Equilateral Triangle. Since all
three sides of an equilateral triangle are equal, the space it occupies can be calculated based on this common side length.
The area is derived from geometric principles, considering the height and base of the triangle, with the result depending on the square of the side length. In practical terms, the area represents the space within the triangle's boundaries.
For example, suppose the side of the area of an equilateral triangle is known. In that case, the area can be computed using a standard method that incorporates the properties of the equilateral triangle. This area is crucial in various applications, from geometry problems to real-world situations involving triangular shapes.
Also Check: Perimeter of a Triangle
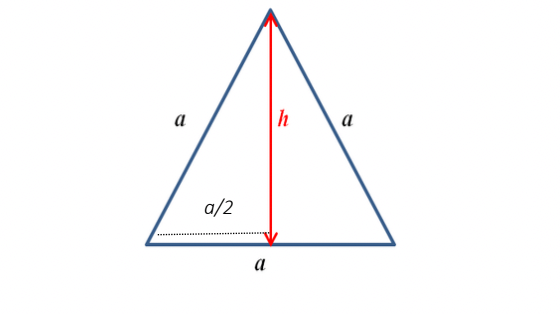
What is an Equilateral Triangle?
An equilateral triangle is a type of triangle where all three sides have equal length . Additionally, all three interior angles in an equilateral triangle are identical, each measuring 60 degrees. This symmetry gives the equilateral triangle its name, as "equilateral" means "equal sides ." Because of these equal sides and angles, an equilateral triangle is highly symmetrical and is often considered the most regular form of a triangle. This type of triangle is commonly found in geometry and is used in various applications, including architecture, design, and mathematics. The equal side lengths and angles also contribute to its properties, such as a specific way to calculate its area. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]Also Check: Triangle
Area of an Equilateral Triangle Formula
The formula for the area of equilateral triangle is: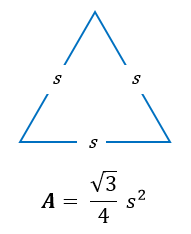
- Using the Standard Triangle Area Formula:
Area=1/2×base×height
where the base is the length of one side of the triangle and the height is the perpendicular distance from the base to the opposite vertex.- Using the Direct Formula for Equilateral Triangles:
A= 3 √ a 2 4
This formula requires only the length of one side of the equilateral triangle and is commonly used for quick calculations.Also Check: Isosceles Triangle
Area of Equilateral Triangle Proof
In an equilateral triangle, all three sides are of equal length, and each of the internal angles measures 60° . The area of equilateral triangle can be calculated when the length of one side is known. The commonly used formula for the area of an equilateral triangle is:Area of equilateral triangle = A = (√3/4)a 2
Where: 𝑎a is the length of each side of the equilateral triangle. This formula for the area of an equilateral triangle can be derived through several methods, each offering a unique approach: Using the General Area of a Triangle Formula: The area of any triangle is generally given by the formulaArea=12×base×height.
Since all sides are equal for an equilateral triangle, the height can be determined using the Pythagorean theorem. Once the height is found, you can substitute it into the area formula to get the desired result. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad.mp4"][/video]Deriving Area of Equilateral Triangle With 2 Sides and Included Angle (SAS)
To derive the area of equilateral triangle using two sides and the included angle, we can apply the Sine Rule for the area of a triangle. The formula for the area of a triangle when two sides and the included angle are known is given by:Area=1/2×𝑎×𝑏×sin(𝐶)
Where:, 𝑎 and 𝑏 are the lengths of the two sides of the triangle. 𝐶 is the included angle between these two sides. For an equilateral triangle, all three sides are equal, and the included angle between any two sides is always 60°. So, in an equilateral triangle: Let 𝑎=𝑏=𝑠 (the side length of the triangle), The included angle, 𝐶=60∘ Substituting into the area formula: Area=12×𝑠×𝑠×sin (60∘) Since, sin(60∘)=32 we can substitute this value into the equation: Area=12×𝑠2×32 Simplifying the expression:Area=3/4×𝑠2
Thus, the area of an equilateral triangle can be derived as:Area=3/4×𝑠2
This matches the standard formula for the area of an equilateral triangle, where 𝑠 is the length of a side. Summary : By using the SAS (Side-Angle-Side) method and applying the Sine Rule, we can derive the formula for the area of an equilateral triangle. The key idea here is to use the fact that all sides are equal and the angle between them is 60°. The area is calculated as34×𝑠243×s 2,
where 𝑠 is the side length of the triangle.
| Related Articles | |
| Integration Formulas | Diameter of a Circle |
| Multiplication Worksheets: | Length Width Height |
Area of Equilateral Triangle FAQs
Why is the formula for the area of an equilateral triangle different from a general triangle?
The formula for the area of an equilateral triangle is specific because all its sides and angles are equal, making it a highly symmetrical shape. This symmetry allows for a simplified formula based solely on the side length.
What happens to the area if the side length of an equilateral triangle is doubled?
If the side length is doubled, the area of the equilateral triangle increases by a factor of area is proportional to the square of the side length. So, if the side length is doubled, the area becomes four times larger.
Are all triangles with 60° angles equilateral triangles?
No, not all triangles with 60° angles are equilateral triangles. While equilateral triangles always have 60° angles, other triangles may have one or two 60° angles but have different side lengths, making them non-equilateral.
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
