First Order Derivative Test : Derivative of any term defines general equation of slope of tangent on it. Slope of tangent on a curve can be either positive negative zero or undefined, first derivative test helps in analysing the graphs such as its local maxima, local minima etc.
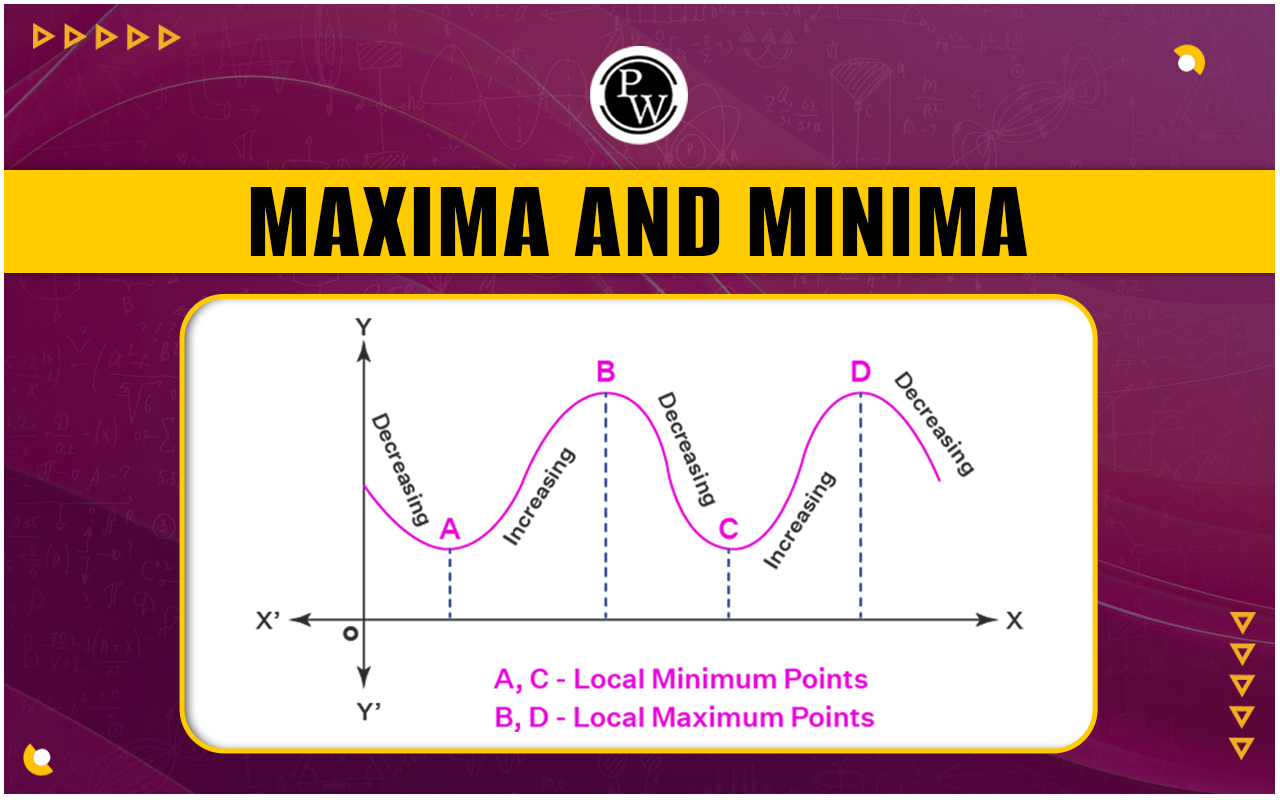
Local maxima of a curve
Local maxima of a curve are defined as set of points on x axis for which slope of tangent is zero or it is the peak point relative to its just left or just right position, it is not necessary for function to be differentiable if finding local maxima.
Local minima of a curve
Local minima of a curve are defined as set of points on x axis for which slope of tangent is zero or it is the lowest point relative to its just left or just right position, it is not necessary for function to be differentiable if finding local minima.
Global maxima of a curve
Global maxima are the highest point on the curve in its domain it is not necessary for the function to be differentiable at the point of global maxima. finding global maxima needs lots of analysis which is out of the scope of first order derivative test.
Global minima of a curve
Global minima are the lowest point on the curve in its domain it is not necessary for the function to be differentiable at the point of global minima. finding global minima needs lots of analysis which is out of the scope of first order derivative test.
Analysis of local maxima and local minima is done on the curves, curves are defined as set of points lying on x - y coordinate plane which is represented in form of algebraic equation and then plotted in xy plane by finding x , y values.
First order derivative test Introduction
First order derivative test: Term must be differentiable for this, first order derivative test is described as
1. Find derivative of the function.
2. Equate the derivative to zero and find all set of points on x axis.
3. Plot the points on number line and use wavy curve method.
4.
For each points check behaviour of derivative if
move from −ve to +ve than that particular point is local minima or if +ve to −ve than that point is local maxima
Let’s have some examples
Examples Based On Wavy Curve Method
Example 1:
Find all points of local maxima and local minima for the curve
and corresponding values?
Sol.
Given curve is
differentiate it with respect to
x
axis
Equate it equal to zero
Plot it in number line
While
is a local maximum as sign changes from + to -, 1 is neither maximum nor minimum.
Local minimum value is put
and
in
Local maximum value is
0
Example 2:
Find local maxima and local minima of the function
?
Sol.
Derivative of the function is
Equate it to zero
In the given interval
exist at
Now left to
is positive and negative right to it
So, function is moving from + to − hence local minima
Rapid Questions Based On Wavy Curve Method
1.
Find local maxima and local minima of the function
?
2.
Find all points of local maxima and local minima for the curve
and corresponding values?
Illustrations based on wavy curve method
1.
Find all points of local maxima and local minima for the curve
and corresponding values?
Sol.
Differentiation of the curve is
equate it to zero
x = 1 is a point of maxima as sign changes from + to –
while x = 3 is a point of minima as sign changes from – to +
Local maximum value is
Local minimum value is
Rapid Questions Based On Wavy Curve Method
1.
Find all points of local maxima and local minima for the curve
and corresponding values?
2.
Find all points of local maxima and local minima for the function
and find the corresponding values?
First Order Derivative Test FAQs
Q.1 : What is Local Maxima?
Q.2 : What are Local Minima?
Q.3 : Function must be differentiable for local maxima and local minim to exist?
Q.4 : Local maxima at a particular point are defined if slope of the curve shifting form positive to negative on it?