Area of a Square Formula: Definition, Characteristics, Solved Examples

Area of a Square Formula: The area of a square refers to the measure of the surface enclosed by The area of a square is determined by multiplying the length of one of its sides by the same length. The unit of measurement for the area is always in square units, such as square meters, square feet, square inches, and square centimeters.

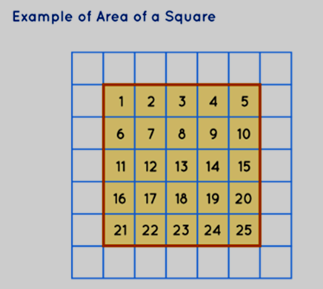
Look at the square shown below. It's made up of 25 smaller squares inside it. This means that the area inside the square is 25 square units. If you take a good look at the square, you will notice that each side of the square is 5 units long. To find the area of the square, you just need to multiply one side by itself. In this case, it's 5 times 5, which equals 25 square units.

Also Check - Complex Number Formula

Area of a Square Formula Characteristics of a Square

A square is a special four-sided shape. It has four sides that are all the same length, and all four angles are right angles, which means they are 90 degrees. Some important things to know about squares are:

• Opposite sides are parallel.
• All sides are of equal length.
• All angles are right angles (90 degrees).

Squares are commonly encountered in everyday objects. Some examples include a chessboard, a clock face, and a blackboard, all of which have square shapes.

Also Check - Conic Section Formula

Area of a Square Formula

The way to find the area of a square when you know the length of one side (S) is with this formula:

Area of a square = Side × Side = S²

In simpler terms, you can find the area of a square by multiplying the length of one side by itself. For example, if a square has a side length of 8 cm, you calculate its area like this:

Area = Side × Side = 8 × 8 = 64 square cm

Also Check - Quadratic Equations Formula

Area of a Square Formula Using the Diagonal

Another method to determine the area of a square is by using the length of its diagonal (d). The formula for finding the area of a square with the diagonal is:

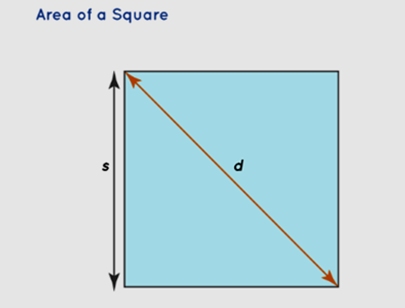
Area of a square using diagonals = Diagonal² / 2

This formula can be derived by applying the Pythagorean theorem to the right triangle formed by half of the diagonal and half of one side. For example, if the diagonal of a square is 12 cm, you can find its area as follows:

Area = (Diagonal × Diagonal) / 2 = (12 × 12) / 2 = 72 square cm

Also Check - Probability Formula

Area of a Square Formula Solved Examples

Example 1: Area of Square when Perimeter is Given

Suppose you have the perimeter of a square and want to find its area. For example, if the perimeter of a square park is 400 ft, you can calculate its area as follows:

Given: Perimeter of the square park = 400 ft

Perimeter of a square = 4 × side

4 × side = 400

Side = 400 / 4 = 100 ft

Area of the square park = side² = 100 × 100 = 10000 square ft

Example: Area of Square When the Side is Given

If the side length of a square is known, finding its area is straightforward. For instance, with a square side of 8 cm:

Given: The square has a side length of 8 centimetres .

Area of the square = side² = 8 × 8 = 64 square cm

Example 3: Area of Square When the Diagonal is Given

When you have the diagonal length of a square, you can use the formula mentioned earlier. For example, with a diagonal of 12 cm:

Given: Diagonal of the square = 12 cm

Area of the square = (Diagonal × Diagonal) / 2 = (12 × 12) / 2 = 72 square cm

Example 4: Area of Square When Perimeter is Given

Suppose the perimeter of a square garden is given as 48 meters, and you want to find its area:

Given: Perimeter of the square garden = 48 meters

Perimeter of a square = 4 × side

4 × side = 48

Side = 48 / 4 = 12 meters

Area of the square garden = side² = 12 × 12 = 144 square meters

Example: Area of Square When the Side is Given

Imagine you have a square tile with a side length of 10 inches, and you want to determine its area:

Given: Side of the square tile = 10 inches

Area of the square tile = side² = 10 × 10 = 100 square inches

Tips for Calculating the Area of a Square

• Keep in mind that to find the area of a square, you just multiply one side by itself. Don't try to double it.
• Always include the unit of measurement when representing the area, as it is a two-dimensional quantity. For instance, if the side is 5 units long, the area is 5 × 5 = 25 square units.