
Conic Section Formula: Conic sections, also known as sections of a cone, are fundamental geometric shapes that arise from the intersection of a plane and a cone. As you mentioned, there are three primary conic sections: the parabola, hyperbola, and ellipse (with the circle being a special case of an ellipse). Let's explore these conic sections in more detail and discuss their common properties, formulas, equations, parameters, and provide some examples:
Also Check - Logarithm FormulaWhat Is the Conic Section?
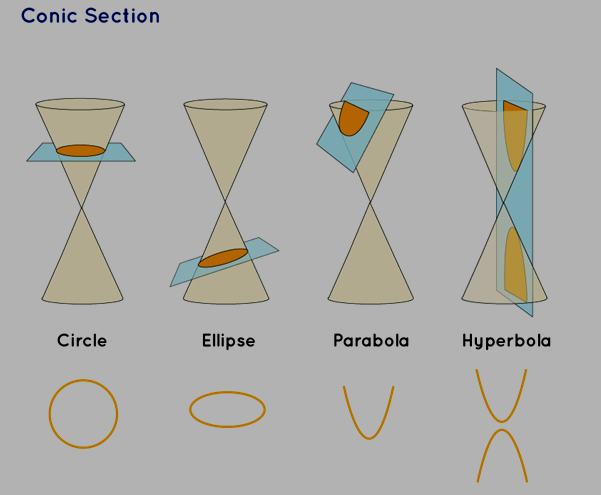
Conic sections are the geometric curves that emerge when a plane intersects a cone. A cone typically consists of two identical conical surfaces known as nappes. The resulting shapes depend on the angle at which the plane intersects the cone and which nappe it intersects. These shapes include:
Circle: When the cutting plane is parallel to the base of the cone, it produces a circular conic section.
Parabola : A parabolic conic section is formed when the intersecting plane slices the cone at an angle.
Ellipse: An elliptical conic section takes shape when the plane intersects the cone at an angle, creating a closed curve.
Hyperbola: Hyperbolic conic sections result when the intersecting plane is parallel to the cone's axis and intersects both nappes of the double cone.
It's important to note that the circle is a special case of an ellipse. These conic sections play a crucial role in geometry and have various real-world applications in mathematics, physics, and engineering.
 Also Check-
Line and Angles Formula
Also Check-
Line and Angles Formula
Conic Section Parameters
The conic sections, including the circle, ellipse, parabola, and hyperbola, are defined and characterized by three fundamental parameters: the focus, directrix, and eccentricity. These parameters play a crucial role in determining the shape and orientation of these conic figures.
Focus: The focus (or foci in the case of ellipses and hyperbolas) is a pivotal point that defines the geometry of a conic section. Each type of conic section has a specific arrangement of foci:
A parabola has one focus.
Ellipses and hyperbolas have two foci.
Circles, a special case of ellipses, have both foci at the same point, resulting in a constant distance from any point on the circle to the focus.
Download PDF Conic Section Formula
Directrix: The directrix is a straight line used to further define conic sections. It is positioned perpendicular to the axis of the referred conic. The relationship between any point on the conic and its distance from the directrix and focus is integral in characterizing the conic section:
A circle does not have a directrix.
A parabola has one directrix.
Both ellipses and hyperbolas have two directrices each.
Eccentricity: Eccentricity (denoted by "e") is a constant ratio that quantifies the distance of a point on the conic section from the focus and directrix. It serves as a unique descriptor of the shape of a conic section and is a non-negative real number. The value of eccentricity determines how closely the conic section resembles a circle:
For a circle, eccentricity (e) is equal to 0.
For ellipses, eccentricity ranges from 0 to less than 1.
Parabolas have an eccentricity of 1.
Hyperbolas have an eccentricity greater than 1.
Understanding these three parameters allows for a precise characterization of conic sections and is essential in various fields of mathematics, science, and engineering.
Also Check - Linear Equation Formula
Terms Related To Conic Section
In addition to the primary parameters of focus, directrix, and eccentricity, conic sections also have several other important parameters that help describe their characteristics. Here's a brief overview of these additional parameters associated with conic sections:
Principal Axis:
Definition: The principal axis is the axis that passes through the center and foci of a conic section. It is also known as the major axis of the conic.
Conjugate Axis:
Definition: The conjugate axis is an axis drawn perpendicular to the principal axis and passing through the center of the conic. It is also referred to as the minor axis.
Center:
Definition: The point where the principal axis and the conjugate axis of the conic intersect is called the center of the conic.
Vertex:
Definition: The point on the principal axis where the conic intersects the axis is known as the vertex of the conic.
Focal Chord:
Definition: The focal chord of a conic is a chord that passes through the focus of the conic section. It intersects the conic section at two distinct points.
Focal Distance:
Definition: The focal distance is the distance of a point on the conic from any of the foci. For ellipses and hyperbolas, which have two foci, there are two focal distances.
Latus Rectum:
Definition: The latus rectum is a focal chord that is perpendicular to the axis of the conic. Its length varies depending on the type of conic:
For a parabola, the length of the latus rectum is LL' = 4a ,
And the length of the latus rectum for an ellipse, and hyperbola is 2b 2 /a.
Tangent:
Definition: A tangent is a line that touches the conic externally at one point. The point where the tangent touches the conic is called the point of contact. From an external point, two tangents can be drawn to the conic.
Normal:
Definition: The normal is a line drawn perpendicular to the tangent and passing through the point of contact and the focus of the conic. There can be one normal for each of the tangents to the conic.
Chord of Contact:
Definition: The chord of contact is drawn to join the points of contact of the tangents drawn from an external point to the conic.
Pole and Polar:
Definition: For a point called the pole located outside the conic section, the locus of the points of intersection of the tangents drawn at the ends of the chords from this point is called the polar.
Auxiliary Circle:
Definition: An auxiliary circle is a circle drawn on the major axis of an ellipse with its diameter. It is used to relate the conic equation of an ellipse to the equation of the circle.
For an ellipse with equation x 2 /a 2 + y 2 /b 2 = 1
For a circle with equation x 2 + y 2 = a 2 .
Director Circle:
Definition: The director circle is the locus of points of intersection of perpendicular tangents drawn to an ellipse.
For an ellipse with equation (x 2 /a 2 + y 2 /b 2 = 1),
the equation of the director circle is x 2 + y 2 = a 2 + b 2
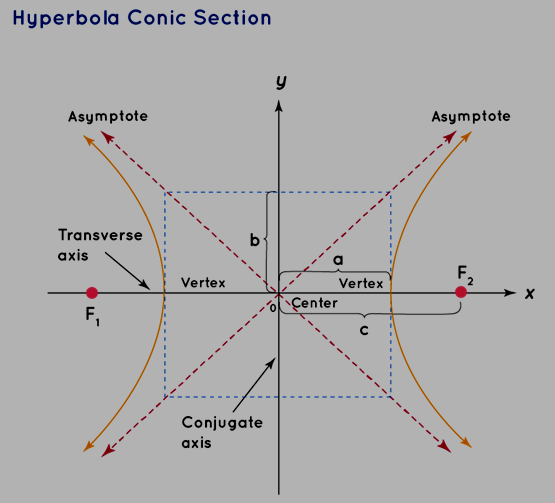
Asymptotes:
Definition: Asymptotes are a pair of straight lines drawn parallel to a hyperbola and assumed to touch the hyperbola at infinity. The equations of the asymptotes for a hyperbola are y = bx/a, and y = -bx/a
These parameters play critical roles in understanding and working with conic sections, helping to define their key characteristics and relationships.
Also Check - Quadrilaterals Formula
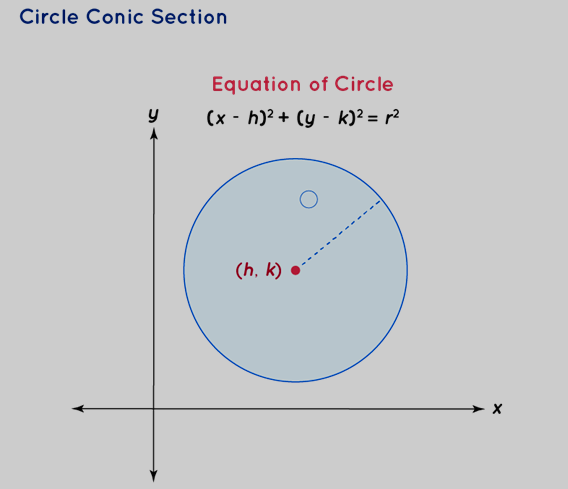
Circle - Conic Section
A circle is a unique variation of an ellipse characterized by a cutting plane that runs parallel to the base of the cone. Within the context of a circle:
The center of the circle coincides with its focus, and this point is often referred to as the center of the circle.
All points on the circle maintain a constant distance from the center, which is known as the circle's radius.
The eccentricity (e) of a circle is precisely zero, highlighting its perfect symmetry.
Unlike other conic sections, a circle does not have a directrix.
The standard equation of a circle with a center at (h, k) and a radius of r is given as:
(x−h) 2 + (y−k) 2 = r 2
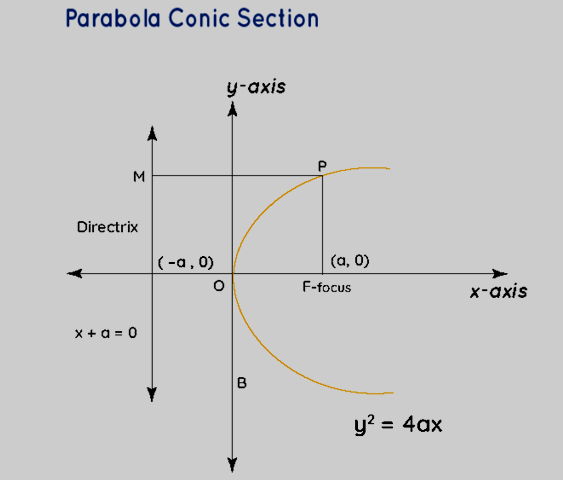
Parabola - Conic Section
When the intersecting plane makes an angle with the surface of the cone, it gives rise to a conic section known as a parabola. A parabola is a distinctive U-shaped curve. Key features of a parabola include:
The eccentricity (e) for a parabola is precisely 1, indicating its unique geometric property.
It is an asymmetrical open plane curve that results from the intersection of a cone with a plane parallel to its side.
In mathematics, the graph of a quadratic function takes the form of a parabola. It is a curve with a line of symmetry and a shape resembling that of the equation y = x^2.
Parabolas can open either upward, like the graph of y = x^2, or downward, like the graph of y = -x^2.
The path of a projectile under the influence of gravity closely follows a parabolic trajectory, making parabolas a fundamental concept in physics and engineering.
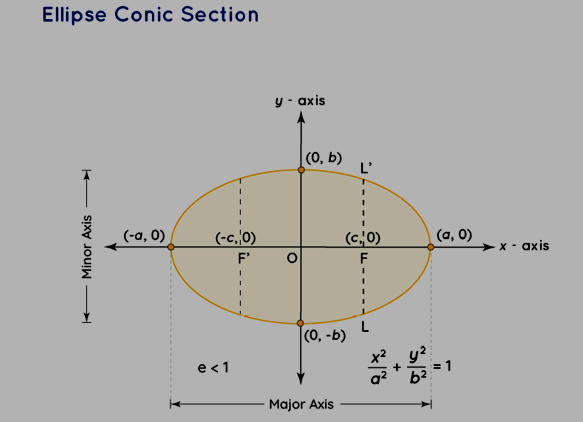
Ellipse - Conic Section
An ellipse emerges as a conic section resulting from the intersection of a plane with a cone at a certain angle. It possesses distinct characteristics, including:
An ellipse is defined by two foci, which are pivotal points that help determine its shape.
It features a major axis and a minor axis, which provide a means to quantify its dimensions.
The eccentricity (e) for an ellipse is a real number less than 1, signifying its deviation from a perfect circle.
An ellipse has two directrices, which are critical in its definition and geometry.
The general equation for an ellipse with its center at (h, k) and lengths of the major and minor axes as '2a' and '2b,' respectively, is a fundamental representation.
The major axis of the ellipse aligns parallel to the x-axis, contributing to its orientation.
(x−h) 2 /a 2 + (y−k) 2 /b 2 = 1
Hyperbola - Conic Section
A hyperbola takes shape when the intersecting plane runs parallel to the axis of the cone and intersects both nappes of the double cone. Some key characteristics of hyperbolas include:
The eccentricity (e) for a hyperbola is greater than 1, reflecting its unique geometric properties.
A hyperbola consists of two separate and unconnected sections, known as branches. These branches are symmetrical mirror images of each other.
The arms of the hyperbola's branches extend diagonally away from each other, approaching the limit of forming a straight line as they move further apart.
A hyperbola serves as an illustrative example of a conic section that arises when a plane intersects a double cone created from two nappes. The general equation for a hyperbola, with its center at (h, k), is expressed as:
(x−h) 2 /a 2 - (y−k) 2 /b 2 = 1
Conic Section Formulas - Standard Forms
Conic section formulas provide the standardized representations of circles, parabola, ellipse, and hyperbola. In these standard forms, the x-axis serves as the principal axis, and the origin (0,0) acts as the center. Key features include:
- Circle: x 2 +y 2 = a 2
- Parabola: y 2 = 4ax when a>0
- Ellipse: x 2 /a 2 + y 2 /b 2 = 1
- Hyperbola: x 2 /a 2 – y 2 /b 2 = 1
Also Check - Data Handling Formula
Conic Sections Formulas Examples
Example 1: To determine the equation of a circle with a center at (4, 3) and a radius of 5
Solution : Using the formula , (x 2 - h 2 ) + (y 2 - k 2 ) = r 2
Substituting values of (h, k) as (4, 3) and r as 5 we get,
= x 2 - 16 + y 2 - 9 = 25
= x 2 + y 2 - 25 = 25
= x 2 + y 2 = 50
Therefore, the equation of the circle is x 2 + y 2 = 50.
Example 2: To find the equation of a parabola with its vertex at the origin (0, 0) and the focus point at (0, 3).
Solution: Vertex of parabola = (0, 0) and Focal point of this parabola = (0, 3)
Since it lies on Y-axis, the axis of this parabola is Y-axis
By using the formula, x 2 = 4ay, we get x 2 = 4(3)y
= x 2 = 12y
Hence, the equation of the parabola is x 2 = 12y.
Applications of Conic Sections
The formulas for conic sections in class 11 mathematics have various practical applications in different fields. Here are some examples:
- Space Science: Conic sections play a significant role in space science. They are used to describe the orbits of celestial bodies such as planets, comets, and satellites. The study of these orbits is crucial for understanding celestial mechanics and planning space missions.
- Antennas and Telescopes: Conic sections are employed in the design of antennas and telescopes. The reflective properties of parabolic dishes, for instance, make them ideal for focusing and capturing signals or light from distant sources.
- Optics: Conic sections are utilized in the design of optical systems, including lenses and mirrors. They help in controlling the path of light, enabling the creation of devices like cameras, microscopes, and binoculars.
- Automobile Headlights: The shapes of automobile headlights often incorporate conic sections to efficiently direct and focus the light produced by the headlights. This enhances visibility for drivers while minimizing light dispersion.
- Flashlights and Reflectors: Conic sections are applied in the design of flashlight reflectors. They help concentrate the light emitted by the bulb into a beam, increasing the flashlight's effectiveness.
- Particle Physics: In the study of atomic and subatomic particles, conic sections can describe the trajectories and interactions of particles in particle accelerators and detectors. Understanding these paths is essential for fundamental research in particle physics.
Conic Section Formula FAQs










