Quadratic Equation Formula: Definition, Properties, Examples

Quadratic Equation Formula denoted as second-degree algebraic expressions, take the form ax ² +bx+ c = 0 . The term "quadratic" originates from the Latin word "quadratus," meaning square. This pertains to the squared nature of the variable x within the equation. In essence, a quadratic equation signifies an "equation of degree 2." The utilization of quadratic equations spans various domains.

Interestingly, quadratic equations find application in diverse scenarios. Notably, when a rocket is launched, its trajectory is delineated by a quadratic equation. Moreover, quadratic equations play a pivotal role in fields such as physics, engineering, and astronomy.

A distinctive characteristic of quadratic equations is that they yield a maximum of two solutions. These solutions can manifest as either real or complex numbers. They are termed as the roots of the quadratic equation, represented as (α, β). Further insights into the roots of quadratic equations will be explored in the subsequent sections.

What is Quadratic Equation?

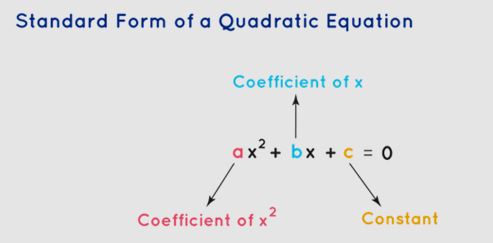
A quadratic equation takes the shape of a second-degree algebraic expression in the variable x. It adheres to the standard format ax ² +bx+ c = 0 , where 'a' and 'b' are coefficients, 'x' represents the variable, and 'c' stands as the constant term. A crucial criterion for an equation to qualify as quadratic is that the coefficient of x ² must not be zero (a ≠ 0). To represent a quadratic equation in the standard format, one lists the x 2 term first, followed by the x term, and concludes with the constant term.

In practical mathematical scenarios, quadratic equations come in diverse presentations. For example: (x - 1)(x + 2) = 0, -x ² = -3x + 1, 5x(x + 3) = 12x, x ³ = x(x ² + x - 3). However, before proceeding with further operations, all of these equations necessitate conversion into the standard form of a quadratic equation.

Roots of a Quadratic Equation

The solutions of a quadratic equation correspond to the two values of 'x' achieved through solving the equation. These solutions, also referred to as the zeros of the equation, signify the points where the equation intersects the x-axis. For instance, considering the equation x ² - 3x - 4 = 0, the solutions are x = -1 and x = 4, as they both satisfy the equation:

When x = -1: (-1) 2 - 3(-1) - 4 = 1 + 3 - 4 = 0

When x = 4: (4) 2 - 3(4) - 4 = 16 - 12 - 4 = 0

Numerous approaches exist to ascertain the solutions of a quadratic equation, with one of these methods involving the use of the quadratic formula.

Download PDF Quadratic Equation Formula

Quadratic Equation Formula

The quadratic formula serves as the most straightforward approach to determining the solutions of a quadratic equation. In instances where quadratic equations are challenging to factorize, the quadratic formula offers a convenient and efficient method to swiftly ascertain the solutions. Within the quadratic formula, both roots are presented in a unified expression. By employing either the positive or negative sign, the two distinct solutions of the equation can be derived interchangeably.

The quadratic formula can be expressed as follows: For a quadratic equation ax ² +bx + c = 0, the roots are obtained using x = [-b ± √( b ² - 4ac)] / 2a

This formula is also known as the Sridharacharya formula.

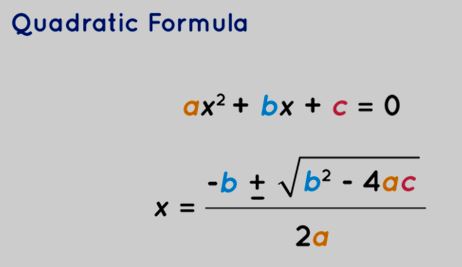
Nature Of Roots Of The Quadratic Equation Formula

The symbols alpha (α) and beta (β) commonly denote the roots of a quadratic equation. In this context, we will delve into methods for determining the characteristics of these roots without explicitly calculating their values.

The nature of the roots of a quadratic equation can be inferred without directly computing the roots themselves (α, β). This can be accomplished by evaluating the discriminant, an integral component of the quadratic equation solution formula. The quantity b ² - 4ac, known as the discriminant of the quadratic equation, is assigned the label 'D'. By analyzing the value of the discriminant, predictions regarding the attributes of the roots of the quadratic equation can be made.

Discriminant: D = b 2 - 4ac

• D > 0, the roots are real and distinct
• D = 0, the roots are real and equal.
• D < 0, the roots do not exist or the roots are imaginary.

Sum And Product Of Roots Of Quadratic Equation Formula

The coefficients of the quadratic equation, namely the term with x 2 , the term with x, and the constant term in ax ² +bx+ c = 0, play a crucial role in determining both the sum and the product of the roots of the quadratic equation. It's possible to directly compute the sum and product of these roots using the equation itself, without needing to explicitly calculate the individual roots.

For a quadratic equation ax ² +bx+ c = 0, the sum and product of its roots can be derived as follows:

Sum of the Roots: α + β = -b/a = Negative Coefficient of x / Coefficient of x ²

Product of the Roots: αβ = c/a = Constant term / Coefficient of x ²

Writing Quadratic Equations Using Roots

A quadratic equation can also be constructed based on the provided roots of the equation. If α and β represent the roots of the quadratic equation, then the corresponding quadratic equation takes the following form:

x ² - (α + β)x + αβ = 0

Formulas Related to Quadratic Equations

Here is a summary of the important formulas that are useful for solving quadratic equations:

• The standard form of a quadratic equation: ax ² +bx + c = 0,
• The discriminant of the quadratic equation: D = b 2 - 4ac.
• For D > 0, the roots are real and distinct.
• For D = 0, the roots are real and equal.
• For D < 0, the roots are imaginary or do not exist.
• Formula for finding the roots of the quadratic equation: x = [-b ± √(b 2 - 4ac)] / 2a.
• Sum of the roots of a quadratic equation: α + β = -b/a.
• Product of the roots of a quadratic equation: αβ = c/a.
• Quadratic equation with given roots α and β: x 2 - (α + β)x + αβ = 0.
• Condition for two quadratic equations to have the same roots: (a1b2 - a2b1)(b1c2 - b2c1) = (a2c1 - a1c2)^2.
• Minimum value of a quadratic expression when a > 0: f(x) = ax ² +bx+ c has a minimum at x = -b/2a.
• Maximum value of a quadratic expression when a < 0: f(x) = ax ² +bx+ c has a maximum at x = -b/2a.
• The domain of any quadratic function encompasses all real numbers.

Methods to Solve Quadratic Equations

A quadratic equation can be resolved to yield a pair of x values, representing the two solutions of the equation. There exist four distinct approaches to determine the roots of a quadratic equation. These four techniques for solving quadratic equations are outlined below:

• Factorization of the Quadratic Equation
• Utilization of the Quadratic Formula (as previously discussed)
• Application of the Completing the Square Method
• Employing the Graphical Method for Root Determination

Let's delve into a comprehensive exploration of each of the aforementioned methods, gaining insight into their utilization, applications, and advantages.

Solving Quadratic Equations by Factorization

The process of factorizing a quadratic equation involves a series of steps. For a quadratic equation in the general form of ax² + bx + c = 0, the initial step is to break down the middle term into two separate terms, in such a manner that the product of these terms equals the constant term. Subsequently, we have the opportunity to extract common factors from the available terms. This eventually leads us to the derivation of the desired factors through the following progression:

x² + (a + b)x + ab = 0

x² + ax + bx + ab = 0

x(x + a) + b(x + a)

(x + a)(x + b) = 0

Method of Completing the Square

The technique of completing the square within a quadratic equation involves performing algebraic operations to square and simplify, ultimately yielding the necessary solutions of the equation. Consider a quadratic equation in the form ax² + bx + c = 0, where 'a' is not equal to 0. To ascertain the roots of this equation, we undertake the following simplification process:

ax² + bx + c = 0

ax² + bx = -c

x² + bx/a = -c/a

Next, we express the left-hand side as a perfect square by introducing a new term, namely (b/2a)², on both sides:

x² + bx/a + (b/2a)² = -c/a + (b/2a)²

(x + b/2a)² = -c/a + b²/4a²

(x + b/2a)² = (b² - 4ac)/4a²

x + b/2a = +√(b² - 4ac)/2a

x = -b/2a + √(b² - 4ac)/2a

x = [-b ± √(b² - 4ac)]/2a

In this context, the '+' sign corresponds to one root, while the '-' sign corresponds to the other root of the quadratic equation. Generally, although this comprehensive method exists, it is often bypassed, and the quadratic formula alone is employed to acquire the necessary roots.

Graphing a Quadratic Equation

Illustrating the quadratic equation ax² + bx + c = 0 graphically involves representing the equation as a function y = ax² + bx + c. By solving the equation and substituting various x values, corresponding y values can be determined, yielding a collection of points. These points can then be plotted on the coordinate axis, resulting in the formation of a parabola-shaped graph that represents the quadratic equation. For more comprehensive insights into graphing a quadratic function.

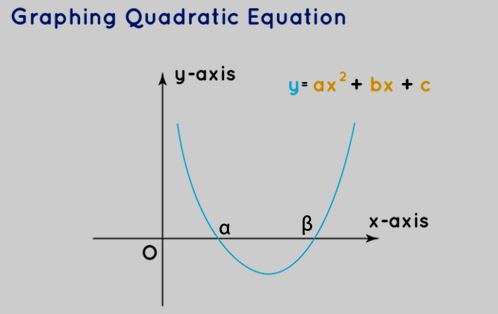
The points where the graph intersects the horizontal x-axis, commonly known as the x-intercepts, coincide with the solutions of the quadratic equation. These points can also be obtained algebraically by setting the y value to 0 in the function y = ax² + bx + c and solving for x.

Quadratic Equations Having Common Roots

Let's examine a pair of quadratic equations sharing common roots: a1x² + b1x + c1 = 0 and a2x² + b2x + c2 = 0. We aim to determine the conditions under which these equations possess a shared root. By solving these two equations, we can derive the prerequisites for their shared root. The equations are solved for x² and x, respectively.

Equation 1: (x²)(b1c2 - b2c1) = (-x)/(a1c2 - a2c1) = 1/(a1b2 - a2b1)

Equation 2: x² = (b1c2 - b2c1) / (a1b2 - a2b1)

Equation 3: x = (a2c1 - a1c2) / (a1b2 - a2b1)

By simplifying the above expressions, we arrive at the subsequent condition that ensures the two equations share a common root:

(a1b2 - a2b1) (b1c2 - b2c1) = (a2c1 - a1c2)²