Competitive Exams

IIT JEE, NEET, ESE, GATE, AE/JE, Olympiad

Only IAS

UPSC, State PSC

School Preparation

Foundation (Class 6-12), Commerce, Arts, CuriousJr (1st - 8th), Science, International Boards

Govt Exam

Judiciary, SSC, Defence, Teaching, JAIIB & CAIIB, BIHAR EXAMS WALLAH, UP Exams, Railway, Nursing Exams, Banking, WB Exams

UG & PG Entrance Exams

MBA, IPMAT, IIT JAM, LAW, CUET UG, UGC NET, GMAT, Design & Architecture, Pharma, CSIR NET, CUET PG, NEET PG

FINANCE

CA, CS, Finance Courses, ACCA

Others

English Wallah, Online Degrees

English Proficiency Test

IELTS, TOEFL

Agriculture

Area of Rhombus Formula: Definition, Derivation and Solved Examples

The area of rhombus formula refers to the space enclosed by this two-dimensional geometric shape. A rhombus itself is a quadrilateral positioned within a two-dimensional (2D) plane, distinguished by its four sides, all of which share the same length and congruency.

Anchal Singh15 Sept, 2023

Area of Rhombus Formula stands as a distinctive variation of a parallelogram, characterized by the presence of two sets of opposite sides that exhibit congruence. This implies that all sides of a rhombus are of equal length. This often leads students to grapple with differentiating between a square and a rhombus. The primary disparity between the two lies in the nature of their internal angles; specifically, all the internal angles of a square are right angles, whereas those of a rhombus do not possess such a characteristic. In the forthcoming discussion, you will acquire a comprehensive understanding of how to determine the area of a rhombus, employing various parameters including diagonals, side and height, and side and internal angle. Each scenario will be elucidated through solved examples to facilitate your comprehension.

What Is The Area Of A Rhombus?

The area of a rhombus formula refers to the space enclosed by this two-dimensional geometric shape. A rhombus itself is a quadrilateral positioned within a two-dimensional (2D) plane, distinguished by its four sides, all of which share the same length and congruency.

Area Of Rhombus Formula

The formula to calculate the area (A) of a rhombus depends on the information you have about the rhombus. Here are the three common methods for finding the area of a rhombus: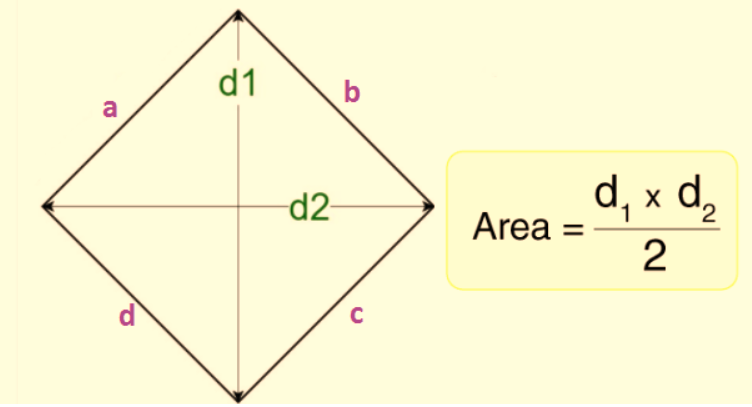 Area of rhombus formula

Using Diagonals (D1 and D2): If you know the lengths of both diagonals (D1 and D2) of the rhombus, you can use the following formula: A = (D1 * D2) / 2 Using Side Length (s) and Height (h): If you know the length of one side (s) of the rhombus and the height (h), you can use the formula: A = s * h The height (h) is the perpendicular distance between two parallel sides of the rhombus.

Also Check - Line and Angles Formula

Using Side Length (s) and Internal Angle (θ): If you know the length of one side (s) of the rhombus and the measure of one internal angle (θ) in degrees, you can use the formula: A = s^2 * (sin(θ)) Here, you need to ensure that θ is in degrees, and you'll use the sine function. Each of these methods allows you to calculate the area of a rhombus, depending on the given information about the rhombus. Choose the appropriate formula based on the data you have.

Derivation for Rhombus Area Formula

To derive the formula for the area of a rhombus, we can break it down into two right triangles. Let's consider a rhombus with side length 's' and diagonals 'D1' and 'D2':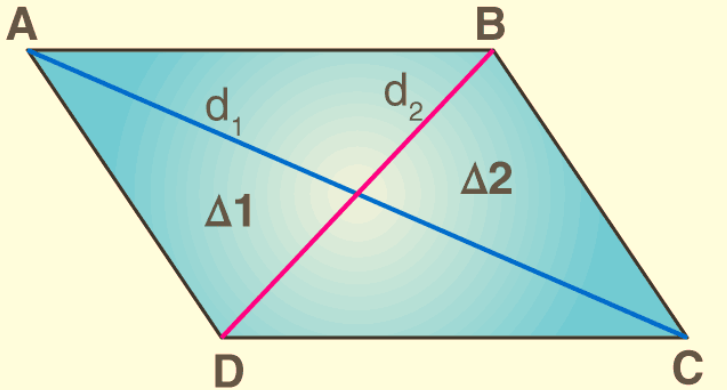

Draw the rhombus with one diagonal (D1) dividing it into two congruent right triangles. Each right triangle has a base equal to half of one diagonal (D1/2) and a height equal to the side length (s) of the rhombus. Use the formula for the area of a triangle: Area of a triangle = (1/2) * base * height For one of the right triangles: Area of one right triangle = (1/2) * (D1/2) * s Now, calculate the total area of the rhombus by considering both right triangles: Total area of rhombus = 2 * Area of one right triangle Total area of rhombus = 2 * [(1/2) * (D1/2) * s] Simplify the expression: Total area of rhombus = (D1/2) * s Since 'D1' is one of the diagonals of the rhombus, and we know that 'D1' is equal to 'D2' (both diagonals are congruent in a rhombus), we can substitute 'D2' for 'D1': Total area of rhombus = (D2/2) * s Finally, you can write the area of the rhombus formula as: Area (A) = (D1 * s) / 2 or Area (A) = (D2 * s) / 2 Both of these formulas represent the area of a rhombus. You can choose the one that suits the given information about the rhombus, whether you know the lengths of the diagonals (D1 and D2) or the side length (s) and a diagonal.

Also Check - Perimeter and Area Formula

How To Calculate Area Of Rhombus?

Below, we will explore three distinct methods for determining the area of a rhombus, accompanied by illustrative examples: Method 1: Utilizing Diagonals Method 2: Employing Base and Height Method 3: Leveraging Trigonometry (specifically, involving a side length and an angle measure)

Also Check - Probability Formula

Area Of Rhombus Using Diagonals: Method 1

Let's examine how to determine the area of a rhombus, such as ABCD, with two diagonals, AC and BD, using the following steps: Step 1: Measure the length of diagonal 1, denoted as d1. This measurement is the distance between points A and C. It's essential to note that the diagonals of a rhombus intersect at the center, forming four right triangles. Step 2: Measure the length of diagonal 2, referred to as d2, which represents the distance between points B and D. Step 3: Multiply the lengths of both diagonals, d1 and d2. Step 4: Divide the result obtained in step 3 by 2. The outcome of this calculation will yield the area of the rhombus ABCD. To illustrate this method further, let's explore it with an example.

Also Check - Linear Inequalities Formula

Example 1: Determining the Area of a Rhombus with Diagonals Measuring 6 cm and 8 cm. Solution: Given: Diagonal 1, d1 = 6 cm Diagonal 2, d2 = 8 cm To compute the area of the rhombus, employ the formula: Area (A) = (d1 × d2) / 2 = (6 × 8) / 2 = 48 / 2 = 24 cm² Therefore, the area of the rhombus is 24 square centimeters (cm²).

Area Of Rhombus Using Base And Height: Method 2

Step 1: Determine both the base and height of the rhombus. The base corresponds to one of the rhombus's sides, while the height signifies the altitude, which is the perpendicular measurement from the selected base to the opposite side. Step 2: Proceed to multiply the base by the calculated height. To illustrate this process, let's explore an example: Example 2: Determine the area of a rhombus with a base measuring 10 cm and a height of 7 cm. Solution: Given: Base, b = 10 cm, Height, h = 7 cm To calculate the area (A), apply the formula: Area (A) = b × h = 10 × 7 cm² A = 70 cm² Hence, the area of the rhombus is 70 square centimeters (cm²).

Area Of Rhombus Using Trigonometry: Method 3

This technique is employed to compute the area of a rhombus when provided with one of its internal angles and the length of one of its sides. Step 1: Begin by squaring the length of any of the sides. Step 2: Follow this by multiplying the squared side length by the sine of the specified internal angle. To grasp a practical application of this approach, let's explore an example demonstrating how to determine the area of a rhombus using the side length and an angle. Example 3: Compute the area of a rhombus with a side length of 2 cm and one of its angles (angle A) measuring 30 degrees. Solution: Given: Side length (s) = 2 cm , Angle A = 30 degrees Square of side = 2 × 2 = 4 To determine the area (A), apply the formula: Area, A = s^2 × sin(30°) A = 4 × 1/2 A = 2 cm² Thus, the area of the rhombus is 2 square centimeters (cm²) when the side length is 2 cm, and angle A is 30 degrees.

Solved Problem On Area Of Rhombus Formula

Problem: Calculate the area of a rhombus with diagonals measuring 10 cm and 12 cm. Solution: Given: Diagonal 1 (D1) = 10 cm Diagonal 2 (D2) = 12 cm Method 1: Using Diagonals Use the formula for the area of a rhombus using diagonals: Area (A) = (D1 * D2) / 2 Plug in the values: Area (A) = (10 cm * 12 cm) / 2 Calculate the area: Area (A) = (120 cm²) / 2 Simplify: Area (A) = 60 cm² So, the area of the rhombus is 60 square centimeters (cm²) when the diagonals are 10 cm and 12 cm long.

Area of Rhombus Formula

What Constitutes a Rhombus?

A rhombus is a type of quadrilateral characterized by opposite sides that are both parallel and of equal length. Additionally, rhombuses possess equal opposite angles, and their diagonals intersect each other at right angles.

What Represents the Formula for Calculating the Area of a Rhombus?

To compute the area of a rhombus, the following formula is employed: A = ½ × d1 × d2

How Can You Determine the Area of a Rhombus Given the Side Length and Height?

To ascertain the area of a rhombus when furnished with the side length and height measurements, utilize this formula: A = Base × Height

What Constitutes the Formula for Calculating the Perimeter of a Rhombus?

The formula for determining the perimeter of a rhombus, with a side length denoted as "a," is: P = 4a units

🔥 Trending Blogs

CBSE Class 10 Compartment Result 2025 Anytime @results.cbse.nic.in

NCERT Solutions Federalism Class 10 Questions and Answers PDF

NCERT Solutions for Gravitation Class 9 Questions Answers PDF

NCERT Ram Lakshman Parshuram Samvad Question Answer for Class 10

NCERT Solutions Atmakatha Class 10 Question Answer Hindi Kshitij

Talk to a counsellorHave doubts? Our support team will be happy to assist you!

7019243492

07019243492

Check out these Related Articles

SCHOOL PREPARATION

CBSE Compartment Result 2025 OUT, Direct Link to Download Here

Read Full Story

1 Aug 2025, 11:54 pm

CLASS 12 EXAM

CBSE Class 12 Compartment Result 2025 Out, Direct Link To Download Marksheet

Read Full Story

1 Aug 2025, 11:54 pm

ICSETEN

ICSE ISC Improvement Results 2025 Out @cisce.org Check 10th 12th Result

Read Full Story

1 Aug 2025, 05:51 pm

SCHOOL

NCERT Solutions Class 11 chemistry Chapter 2 Structure of atom

Read Full Story

1 Aug 2025, 05:49 pm

CLASS 6 EXAM

NCERT Class 6 Maths Ganita Prakash Chapter 9 Symmetry PDF

Read Full Story

31 Jul 2025, 01:36 pm

CLASS 7 EXAM

NCERT Solutions for Class 7 Maths Ganita Prakash Chapter 3 PDF

Read Full Story

30 Jul 2025, 12:49 pm

CLASS 7 EXAM

NCERT Solutions for Class 7 Science Curiosity Chapter 7

Read Full Story

30 Jul 2025, 05:07 pm

CLASS 7 EXAM

NCERT Solutions for Class 7 Science Curiosity (2025-26 Edition)

Read Full Story

25 Jul 2025, 02:18 pm

CLASS 7 EXAM

NCERT Solutions for Class 7 Science Curiosity Chapter 9 Life Processes in Animals

Read Full Story

11 Jul 2025, 07:00 pm

Join 15 Million students on the app today!

Live & recorded classes available at ease

Dashboard for progress tracking

Millions of practice questions at your fingertips

Free Learning Resources

PW Books

Notes (Class 10-12)

Class 10 Math's Notes

Class 10 Chemistry Notes

Class 10 Physics Notes

lass 10 Biology Notes

Aptitude & Reasoning

Class 10 Geography

Physics Class 11 Notes

Class 11 Chemistry Notes

Maths Notes Class 11

Zoology Class 11

Class 11 Botany Notes

Physics Class 12 notes

Chemistry Class 12

Maths Notes Class 12

Zoology class 12

Class 12th Botany Notes

PW Study Materials

Arjuna JEE Study Material

JEE 5 PYQs

JEE Mind Maps

Yakeen Study Material

NCERT Punch

Arjuna Neet Study Material

NEET PYQs

CBSE Sample Paper

CBSE Question Bank

Udaan For Class 10th Study Material

Notes (Class 6-9)

Class-6 Theory & Notes

Math's Notes for class 7

Science Notes for class 7

Class 8 Math Notes

Class 8 Chemistry Notes

Class 8 Physics Notes

Class 8 Biology Notes

Class 8 SST Notes

Class 9 Math's Notes

Class 9 Physics Notes

Class 9 Chemistry Notes

Class 9 Biology Notes

Ncert Solutions

NCERT Solutions For Class 6

NCERT Solutions For class 7

NCERT Solutions for class 8

NCERT Solutions for class 9

NCERT Solutions for class 10

NCERT Solutions for class 11

NCERT Solutions for Class 12

NCERT Solutions For Class 6

Govt Exams

Entrance Exams

Our Other Websites

Class 6th to 12th Online Courses

Class 12 Online Course

Class 11 Online Course

Class 10 Online Course

Class 9 Online Course

Class 8 Online Course

Govt Job Exams Courses

SSC Online Coaching

Bank Exam Online Coaching

TET Online Coaching

JAIIB & CAIIB Online Coaching

Bihar Exam Online Coaching

UPSC Coaching

UPSC Online Coaching

UPSC Offline & Hybrid Coaching

State PSC Online Coaching

UPPSC Online Coaching

BPSC Online Coaching

Defence Exam Coaching

NDA Online Coaching

CDS Online Coaching

AFCAT Online Coaching

Agniveer Online Coaching

Gate Exam Coaching

Civil Engineering Courses

Mechanical Engineering Courses

Formulas

Other Exams

Company Secretary Exam

Know about Physics Wallah

Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.

We Stand Out because

We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.

Our Key Focus Areas

Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.

What Makes Us Different

Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others

What Is The Area Of A Rhombus?

Area Of Rhombus Formula

The formula to calculate the area (A) of a rhombus depends on the information you have about the rhombus. Here are the three common methods for finding the area of a rhombus: Area of rhombus formula

Also Check - Line and Angles Formula

Derivation for Rhombus Area Formula

To derive the formula for the area of a rhombus, we can break it down into two right triangles. Let's consider a rhombus with side length 's' and diagonals 'D1' and 'D2':