
Hexagonal Pyramid Formula: The hexagonal pyramid represents a unique variation among pyramids. It features a hexagonal base and is constructed by joining isosceles triangles, converging at the apex. This article aims to explore and deepen our understanding of the hexagonal pyramid concept.
Hexagonal Pyramid Formula
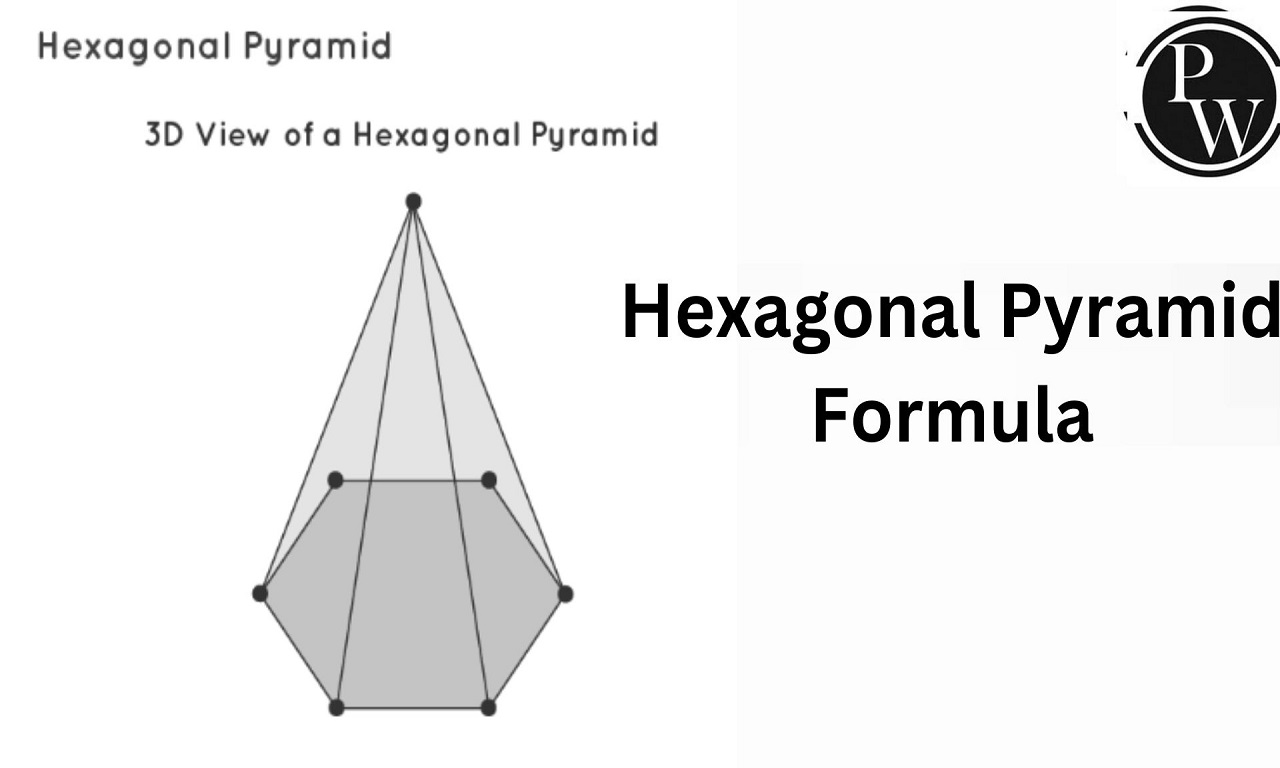
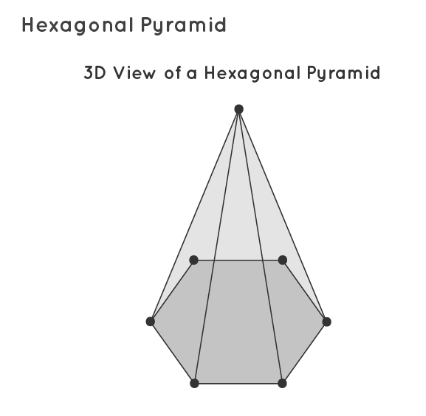
A hexagonal pyramid is a three-dimensional geometric figure characterized by a base in the shape of a hexagon and triangular faces, typically isosceles triangles, meeting at the apex or top of the pyramid. Comprising a base with six sides and six isosceles triangular lateral faces, a hexagonal pyramid is also referred to as a heptahedron. This structure includes seven faces, twelve edges, and seven vertices. Refer to the image below for a visual representation of a hexagonal pyramid.
Hexagonal Pyramid Formula Volume
Determining the Volume of a Hexagonal Pyramid involves considering three critical dimensions: the apothem (measured from the base's center to any side), the base length, and the pyramid's height from the apex to the base. The formula to calculate the volume of a hexagonal pyramid is:
Volume of Hexagonal Pyramid = (abh) cubic units
Where:
a represents the apothem of the pyramid
b signifies the base
h denotes the height
In cases where the apothem of the hexagonal pyramid isn't specified and the triangles are equilateral, an alternative formula is used.
The formula for the volume of a hexagonal pyramid is expressed as (√3/2) × a² × h cubic units, where 'a' represents the side length of the base, and 'h' indicates the height of the hexagonal pyramid
Hexagonal Pyramid Formula Surface Area
Surface Area of a Hexagonal Pyramid requires knowledge of its base and the slant height, which is the measurement from the apex to any point on the base's boundary. Here are the formulas for the base area and surface area of the hexagonal pyramid:
Base Area of a Hexagonal Pyramid = 3ab square units
Surface Area of a Hexagonal Pyramid = (3ab + 3bs) square units
Where:
a signifies the apothem of the pyramid
b represents the base
s stands for the slant height of the pyramid
Hexagonal Pyramid Net
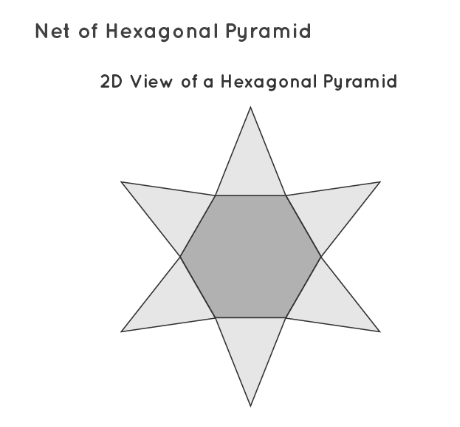
With 7 faces, 7 vertices, and 12 edges, the hexagonal pyramid displays a net configuration. This net is constructed from a base shaped like a hexagon comprising 6 sides, around which 6 triangles emerge by connecting the base's edges. These triangles constitute the lateral faces of the pyramid. Upon flattening the pyramid, the net reveals 6 triangles and one hexagonal base, totaling 6 faces for the triangles and one face for the base. Please refer to the image below for visual clarification.
Properties of a Hexagonal Pyramid
Similar to other pyramids, a hexagonal pyramid possesses distinct characteristics setting it apart. Here are its defining properties:
- The base of a hexagonal pyramid is in the shape of a polygon known as a hexagon.
- Consisting of 6 isosceles triangles, these faces stand upright against the base and converge at the apex.
- This type of pyramid features a total of 7 vertices, with 6 positioned at the base and one at the peak.
- A hexagonal pyramid is composed of 12 edges, 6 connecting the edges of the triangles to the central vertex and the other 6 edges belonging to the base.
- In total, the hexagonal pyramid encompasses 7 faces, with each representing a side of the triangle and the additional base.
The hexagonal pyramid stands as a distinctive geometric form among pyramids, distinguished by its hexagonal base and triangular faces converging at the apex. This exploration aimed to deepen our understanding of this unique structure. Defined by a base with six sides and isosceles triangular lateral faces, the hexagonal pyramid. It is also known as a heptahedron, embodies seven faces, twelve edges, and seven vertices. Its characteristics, such as the base shape, the arrangement of faces, and vertex count, differentiate it within the field of pyramids.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Tangent Line Formula | Tangent to a Circle Formula |
| Tangent 3 Theta Formula | Tan Theta Formula |
Hexagonal Pyramid Formula FAQs
What is a hexagonal pyramid?
How do you find the volume of a hexagonal pyramid?
What is the surface area formula for a hexagonal pyramid?
What are the properties of a hexagonal pyramid?
Why is the hexagonal pyramid unique?












