
Tangent to a Circle Formula :A line touching a circle at a single point is called a tangent, and this point is referred to as the point of tangency. At this intersection, the tangent is perpendicular to the circle's radius. Tangents can relate to other curved shapes, each with its unique equation, explored below in this article.
Tangent to a Circle Formula
A tangent to a circle contacts the circle at only one point, with just one tangent existing at any specific circle point. The point where the tangent meets the circle is termed the point of tangency. At their intersection point, it can be shown that the tangent and the circle's radius are perpendicular to each other.
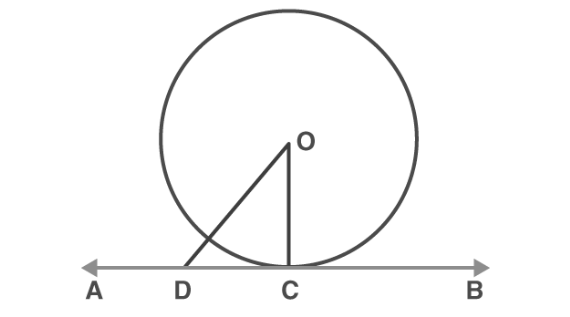
Consider the circle depicted in the figure above, with its center marked as O. AB represents the tangent to the circle passing through point C.
Choose a point D on the tangent line AB, distinct from point C, and connect it to O to form line segment OD. Point D must be situated outside the circle; if it were inside the circle, AB would become a secant, not a tangent.
Consequently, OD is longer than the radius OC of the circle. This holds true for all points along AB except for the point of contact, C. It follows that OC represents the shortest distance between the center of the circle O and the tangent AB.
Since the shortest distance between a point and a line is the perpendicular distance between them, it can be deduced that OC is perpendicular to AB.
In summary:
The tangent intersects the circle at only one point.
The line containing the radius through the point of contact is termed the 'normal' to the circle at that point.
Note: A tangent to a circle represents a specific case of a secant when the endpoints of the corresponding chord coincide.
Tangent to a Circle Formula General Equation
Below is the provided list of Tangent to a Circle Formula Equations:
The equation for the tangent to a circle x 2 + y 2 =a 2 at (x 1 , y 1 ) is xx 1 +yy 1 = a 2
The equation for the tangent to a circle x 2 + y 2 +2gx+2fy+c =0 at (x 1 , y 1 ) is xx 1 +yy 1 +g(x+x 1 )+f(y +y 1 )+c =0
The equation for the tangent to a circle x 2 + y 2 =a 2 at (a cos θ, a sin θ ) is x cos θ+y sin θ= a
The equation for the tangent to a circle x 2 + y 2 =a 2 for a line y = mx +c is y = mx ± a √[1+ m 2 ]
Tangent to a Circle Formula Conditions
The condition for establishing a tangent is contingent upon its contact with a curve at a solitary point; otherwise, it is simply regarded as a line. Hence, the conditions for defining a tangent are based on the location of the point of tangency in relation to the circle:
- If the point is within the circle.
- If the point is on the circle.
- If the point is outside the circle.
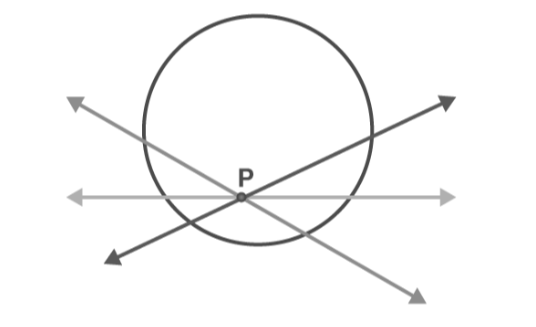
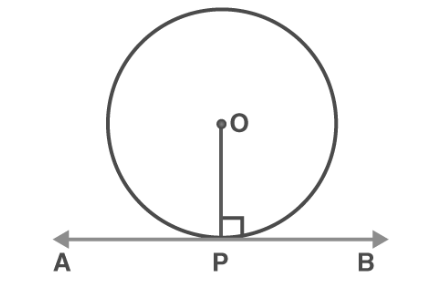
If the point is within the circle
Examining point P situated inside the circle in the preceding figure, it is evident that any line passing through P intersects the circle at two distinct points. Consequently, it can be inferred that it is impossible to draw a tangent to a circle that passes through a point located inside the circle.
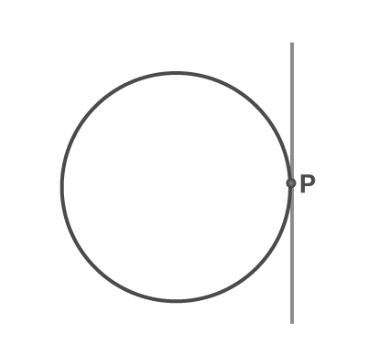
If the point is on the circle
The illustration demonstrates that there exists a single tangent to a circle when passing through a point situated on the circle itself.
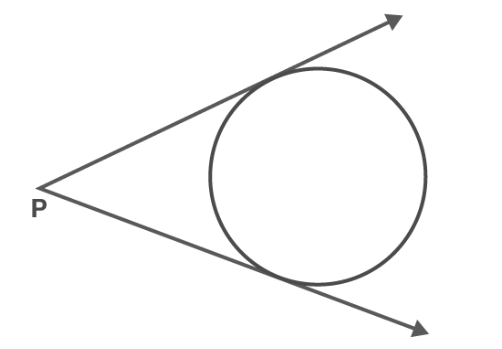
If the point is outside the circle
According to the figure above, it can be stated that a point situated outside the circle allows for the existence of precisely two tangents to the circle from that point.
Tangent Formula
Assume a point P is situated outside the circle. Drawing two tangents from point P, meeting at points A and B on the circle. Let a secant be drawn from P, intersecting the circle at Q and R. PS represents the tangent line from point P to S. The formula for the tangent to a circle and the circle's secant can be represented as follows:
Tangent to a Circle FormulaPR/PS = PS/PQ
PS 2 =PQ.PR
Tangent to a Circle Formula Theorem
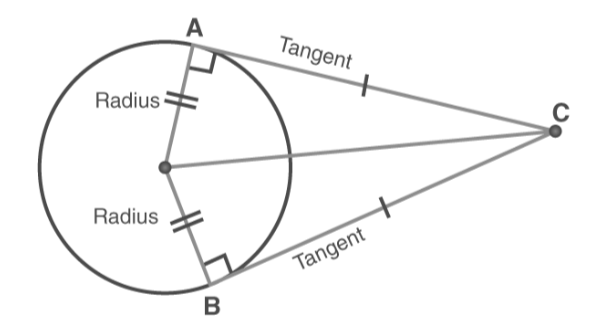
Theorem 1: The statement is as follows. The tangent touching a circle is perpendicular to the circle's radius at the point of contact.
Theorem 2: When two tangents are drawn from an external point to a circle, both tangents are of equal length.
Tangent to a Circle Formula Properties
The tangent makes contact with the circle at only one point.
At the point of tangency. It is perpendicular to the circle's radius
The tangent never intersects the circle at two points.
The lengths of tangents from an external point to a circle are identical.
| Related Links | |
| Vector Projection Formula | Variance Formula |
| Unit Rate Formula | Uniform Distribution Formula |
Tangent to a Circle Formula FAQs
What is a tangent to a circle?
What are the conditions for tangency with a circle?
What are the key properties of tangents to a circle?
Are there any fundamental theorems related to tangents?










