
Tan Theta Formula: The tangent function, part of Trigonometry, a mathematical branch focusing on angle-related functions, explores the correlation between angles and side lengths within triangles. It primarily aids in determining unknown angles or side lengths within right-angled triangles using specific trigonometric functions and formulas. Trigonometry encompasses six widely utilized functions: Sine (sin), Cosine (cos), Tangent (tan), Cotangent (cot), Secant (sec), and Cosecant (cosec). This discussion centers on the formula for tan θ.
Tan Theta Formula
Tan θ, one of the six primary trigonometric functions, is also known as the tangent law. This function, in the context of a right-angled triangle, is defined as the ratio between the side opposite the angle and the adjacent side. Alternatively, it can be expressed as the ratio of the sine of an angle to its cosine.
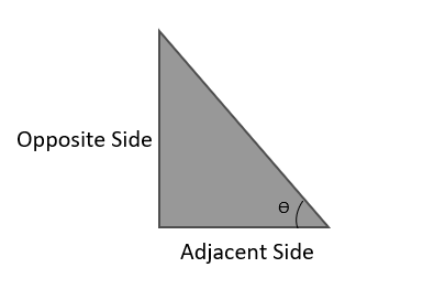
tan θ = Opposite side/Adjacent side
where.
θ is one of the acute angles.
| θ | 0° | 30° | 45° | 60° | 90° |
| tan θ | 0 | 1/√3 | 1 | √3 | ∞ |
Important Tan Theta Formula
Below are some Important Tan Theta Formulas.
tan(θ)=sin(θ)/cos(θ)
tan(θ)=1/cot(θ)
tan2(x)=sec2(x)-1
tan(-x)=-tan(x)
tan(90o-x)=cot(x)
tan(x+π)=tan(x)
tan(π-x)=-tan(x)
tan(x+y)= \frac{tan(x)+tan(y)}{1-tan(x).tan(y)}
tan(x-y)= \frac{tan(x)-tan(y)}{1+tan(x).tan(y)}
tan(2x)=\frac{2tan(x)}{1-tan^2(x)}
tan(3x)=\frac{3tan(x)-tan^3(x)}{1-3tan^2(x)}
tan(x/2)=\sqrt{\frac{1-cos(x)}{1+cos(x)}}
Tan Theta Formula Solved Examples
Example 1: Finding θ in a Right-Angled Triangle
Solution: Given: Opposite side length = 3 cm
Adjacent side length = 3√3 cm
Using the tangent rule:
tan(θ)= Opposite side / Adjacent side
= 3 / 3√3
= 1 / √3
tan ( 3 0 ∘ ) = 1 / √3
tan(30 ∘ )=1 / √3
Therefore, θ=30 ∘ .
Example 2: Determining tanθ from cotθ=0
Solution: Given: cotθ=0
As the relationship between tanθ and cotθ is inverse:
tanθ= 1/ cotθ = 1/ 0
tanθ=∞
Example 3: Finding tan tanθ from sinθ= 1/2 and cosθ= √3/2.
Solution: Given: sinθ= 1/2
cosθ= √3/2.
Using the relationship
tanθ= sinθ / cosθ :
tanθ= (1/2 ) / (√3/2) = 1 / √3
Example 4: Determine tanx from secx= 2/5
Solution:
Given: secx= 2 /5
Using the identity sec 2 x−tan 2 x=1 and
tan 2 x=sec 2 x−1:
tan 2 x=( 2/5 ) 2 −1= 4/25 −1 = 4−25 / 25 =− 21 /25
tan(x) = √(-21/25)
tan(x) = √(-21)/5
Example 5: Determine tanx from secx= 1/5
Solution:
Given: secx= 1 /5
Using the identity sec 2 x−tan 2 x=1 and
tan 2 x=sec 2 x−1:
tan 2 x=( 1/5 ) 2 −1= 1/25 −1 = (1−25) / 25 =− 24 /25
tan(x) = √(-24/25)
tan(x) = √(-24)/25
Example 6: Finding tan tanθ from sinθ= 1/ √2 and cosθ= √3/2.
Solution: Given: sinθ= 1/ √2
cosθ= √3/2.
Using the relationship
tanθ= sinθ / cosθ :
tanθ= (1/ √2 ) / (√3/2) = √2 / √3
Example 7: Finding tan tanθ from sinθ= 1 and cosθ= √3/2.
Solution: Given: sinθ= 1
cosθ= √3/2.
Using the relationship
tanθ= sinθ / cosθ :
tanθ= (1 ) / (√3/2) = 2 / √3
Example 8: Determine tanx from secx= 1/3
Solution:
Given: secx= 1 /3
Using the identity sec 2 x−tan 2 x=1 and
tan 2 x=sec 2 x−1:
tan 2 x=( 1/3 ) 2 −1= 1/9 −1 = (1−9) / 9 =− 8/9
tan(x) = √(-8/9)
tan(x) = √(-8/9)
The tangent function, an important aspect of trigonometry, serves to establish the relationship between angles and side lengths within triangles, particularly in right-angled triangles. It aids in determining unknown angles or side lengths using specific trigonometric functions and formulas. The fundamental formula for tan θ involves the ratio of the side opposite an angle to the adjacent side.
Throughout various problem-solving scenarios, the tangent function has been applied to find unknown angles or ratios. From identifying angles using known side lengths to solving for tangent values when given information about other trigonometric functions like sine, cosine, and secant, the application of the tangent function is crucial in trigonometric problem-solving.
Understanding the fundamental principles and relationships between trigonometric functions like tangent, sine, cosine, cotangent, secant, and cosecant, as well as their respective formulas, enables precise calculations and analysis within trigonometry, particularly in the context of right-angled triangles.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Pythagorean Triples Formula | Quadratic Interpolation Formula |
| Quartile Formula | Recursive Formula |
Tan Theta Formula FAQs
What is the fundamental Tan θ formula?
What does the tangent function represent in a right-angled triangle?
What's the relationship between tangent and cotangent?
What is the difference between tan(−x) and −tan(x)?
How does tan(x+y) relate to tan(x) and tan(y)?










