Orthocenter Formula, Definition, Solved Example
Manoj Kumar4 Nov, 2023
Share
The term "ortho" derives from "right." The orthocenter formula signifies the centre point related to all right angles within a triangle. This formula is constructed from the vertices to the opposite sides, known as altitudes. Understanding this concept is crucial for grasping the diverse properties of a triangle concerning its additional dimensions. An altitude of a triangle is a line passing through a vertex and perpendicular to the opposite side. Hence, every vertex of a triangle forms altitudes. Let's delve further into the details of the orthocenter formula.
What is the Orthocenter Formula
The point of intersection of a triangle's altitudes is termed the orthocenter. This formula aids in determining the coordinates of the triangle's orthocenter. Let's explore the details of the orthocenter formula.
We will examine a triangle PQR, shown in the figure below.
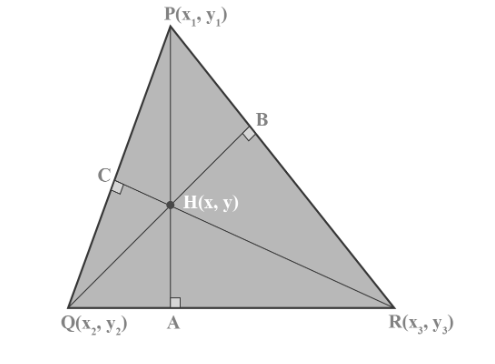PA, QB, and RC denote the perpendicular lines drawn from the three vertices: P( x
1
, y
1
), Q( x
2
, y
2
), and R( x
3
, y
3
) respectively of triangle △PQR. H( x, y) represents the point where the three altitudes of the triangle intersect.
Step 1: To calculate the slope of the triangle's sides using the formula:
The slope is calculated using the formula:
m(slope)= ( y 2 −y 1 )/ (x 2 −x 1 )
Let the slope of PR be denoted as mPR. Therefore, mPR= ( y 3 −y 1 ) / (x 3 −x 1 ) Similarly, mQR= ( y 3 −y 2 ) / (x 3 −x 2 ) Step 2: The slope of the altitudes of triangle △PQR will be perpendicular to the slope of its sides. The perpendicular slope of a line is given by: Perpendicular slope of line = − 1/ slope of the line = =−1/ m The slope of the respective altitudes is: Slope of PA: mPA= − 1/ mQR Slope of QB: mQB= −1/ mPR We will utilize the slope-point form equation for a straight line to derive the equations of the lines that coincide with PA and QB. The general equation formed using arbitrary points x and y is:mPA= (y−y 1 ) / (x−x 1 )
mQB= (y−y 2 ) / (x−x 2 )
By solving these equations for any given values, the orthocenter of a triangle can be determined. This method, outlined step-by-step in the formula, allows for the accurate computation of coordinates defining the orthocenter. Its applications not only aid in geometrical problem-solving but also facilitate a deeper understanding of the fundamental properties of triangles in the realm of mathematics.Orthocenter Formula Solved Example
Example 1: Finding the orthocenter of a triangle with vertices A(1, 3), B(2, 5), C(3, -4) using the orthocenter formula. The triangle is denoted as ABC with the orthocenter H.
Solution: Given the vertices of the triangle: A(1,3) B(2,5) C(3,−4) Let the coordinates of the orthocenter be H(x, y). Using the orthocenter formula: Slope of AB: m AB = ( y 2 −y 1 )/ (x 2 −x 1 ) = (5−3) / (2−1) =2 Slope of CF: m CF =Perpendicular slope of AB=−1/ m AB =−1/ 2 The equation of CF is given by: (y−y 1 )=m(x−x 1 ) y+4= −1/ 2 (x−3) 2y+8=−x+3 x+2y=−5(equation 1) Slope of BC: m BC = ( y 2 −y 1 ) / (x 2 −x 1 ) = (−4−5)/ (3−2) =−9 Slope of AD: m AD =Perpendicular slope of BC=− 1 / m BC = 1 / 9 The equation of AD is given by: (y−y 1 )=m(x−x 1 ) y−3= 1/9 (x−1) 9y−27=x−1 x−9y=−26(equation 2) Subtracting equation (2) from (1), y= 21 / 11 . Substituting this value into equation (1): x=−97 /11 Join Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.| Related Links | |
| Hexagonal Pyramid Formula | Hypothesis Testing Formula |
| Interquartile Range Formula | Inverse Variation Formula |
Orthocenter Formula FAQs
What does the orthocenter of a triangle represent?
How is the orthocenter formula defined?
What are altitudes in a triangle?
Why is the orthocenter of significance in triangles?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
