
Inverse Variation Formula: Inverse variation denotes a proportional relationship where one quantity's increase results in the decrease of another, and vice versa. This relationship signifies that as one quantity increases, the other decreases, ensuring their product remains constant—the constant of proportionality. Real-life examples of inverse variation are abundant. Consider a car's speed: as it accelerates, the time taken to reach a destination decreases. This article aims to delve into the concept of inverse variation, exploring its formula, graphical representation, and providing multiple illustrative examples.
Inverse Variation
Inverse Variation Formula is xy=k. Inverse variation refers to a relationship between two quantities that exhibit an inverse correlation. In the field of proportionalities, there exist two primary types: direct variation and inverse variation. Direct variation occurs when a change in one quantity results in a corresponding change in the other quantity, be it an increase or decrease. Conversely, inverse variation describes a scenario where one quantity's increase coincides with the decrease of the other quantity.
Inverse Variation Formula
When the product of two non-zero quantities remains constant (known as the constant of proportionality), they are deemed to be inverse variation. Put differently, two quantities exhibit inverse variation when one is directly proportional to the reciprocal of the other. Hence, an increase in one quantity results in a decrease in the other, and conversely, a decrease in one quantity corresponds to an increase in the other.
The symbol "∝" denotes proportionality. In the case of two quantities, x and y, exhibiting Inverse Variation Formula denoted as:
x∝ 1/ y or y∝ 1/ x .
To formulate this as an equation, a constant or coefficient of proportionality, represented by k, is introduced. Thus, the equation for Inverse Variation Formula is presented as:
x= k/y or
y= k/x ,
xy=k.
Here, k stands for the constant of proportionality, and it's important to note that x ≠ 0 =0 and y ≠ 0.
Product Rule for Inverse Variation:
Consider two sets of solutions for inverse variation:
(x1, y1) and (x2, y2).
This relationship can be expressed as x 1 ⋅y 1 =k and x 2 ⋅y 2 =k.
Using these equations:
x 1 ⋅y 1 =x 2 ⋅y 2
or
x 1 / x 2 =y 2 / y 1
This demonstrates the product rule for inverse variation. Let's illustrate this formula for inverse variation using an example.
Inverse Variation Formula Solved Example
Example: Let's consider x and y in an inverse proportion such that when x = 15, y = 4. We're tasked to find the value of y when x = 20.
Solution: Given: x 1 =15, y 1 =4, x 2 =20, y 2 =?
Utilizing the inverse variation formula, x 1 ⋅y 1 =x 2 ⋅y 2
Substituting the provided values, 115×4=20×y 2
60=20×y 2
y 2 =3
Answer: Hence, the value of y is 3 when x equals 20.
Graph of Inverse Variation
The graphical representation of an inverse variation takes the form of a rectangular hyperbola. When two quantities, x and y, exhibit inverse variation, their product equals a constant, denoted as k. Since neither x nor y can equal zero, the graph does not intersect the x-axis or y-axis. The graph for an inverse variation with the function y = k / x is depicted below:
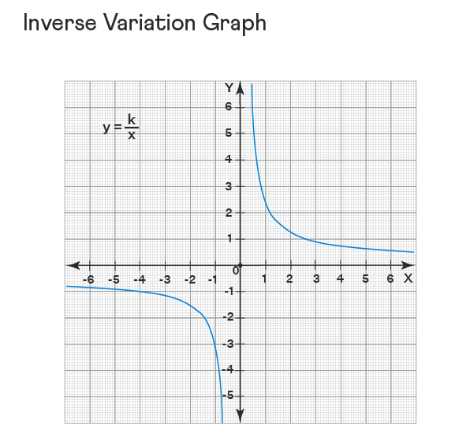
Key Points about Inverse Variation
- When one quantity increases while the other decreases, or vice versa, it indicates an inverse variation between the two quantities.
- An inverse variation is denoted as x∝ 1/y or x= k/y .
- For two quantities in inverse variation, it's crucial that both values are not equal to zero, and their product remains constant (the constant of proportionality).
- The relationship between two quantities exhibiting inverse variation produces a rectangular hyperbola on the Cartesian coordinate plane.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Tangent Line Formula | Tangent to a Circle Formula |
| Tangent 3 Theta Formula | Tan Theta Formula |
Inverse Variation Formula FAQs
What is inverse variation?
What's the inverse variation formula?
How do you express inverse variation as an equation?
What does the constant 'k' represent in inverse variation?










