Introduction to Truss, Classification, Types

Introduction to Truss

In engineering mechanics, the study of structures is crucial as it forms the foundation for understanding how various mechanical components interact and support loads. Structures are an integral part of engineering systems, ranging from simple trusses to complex bridges and buildings. A structure is an assembly of several members connected such that these bodies don’t have any relative motion between them to carry and distribute loads safely and efficiently.

Truss

Trusses are fundamental structural elements extensively used in civil and mechanical engineering to carry and distribute loads efficiently. Trusses are commonly used in bridges, roofs, transmission towers and other load-bearing structures due to their efficient load distribution capabilities and cost-effectiveness.

• The concept of a truss is derived from the remarkable stability of a basic triangular formation. A triangle stands as the simplest geometric shape that maintains its form under the application of load when the lengths of its sides remain fixed.
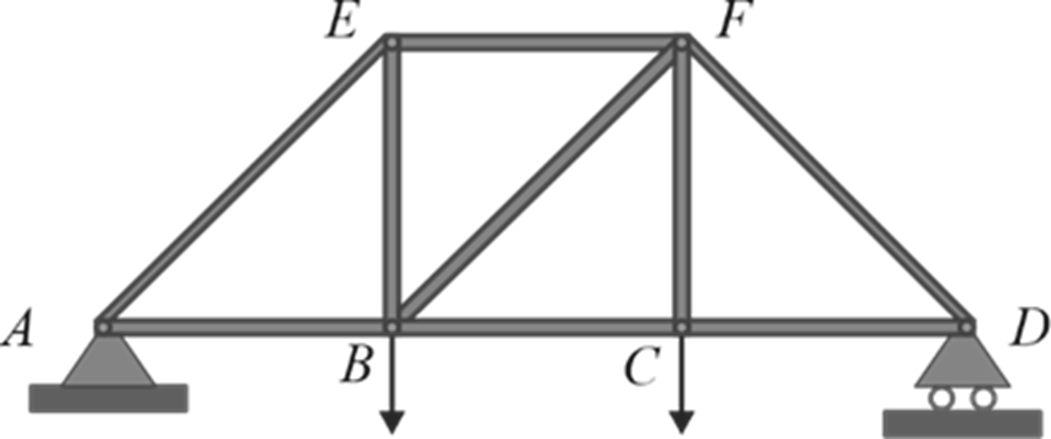
• A truss is a structure that is made of straight slender bars joined together at their ends by frictionless pins to form a pattern of triangle.

• The loads exclusively apply to the joints and not the members. As a result, each member of a truss is classified as a two-force member.

Classification of Trusses

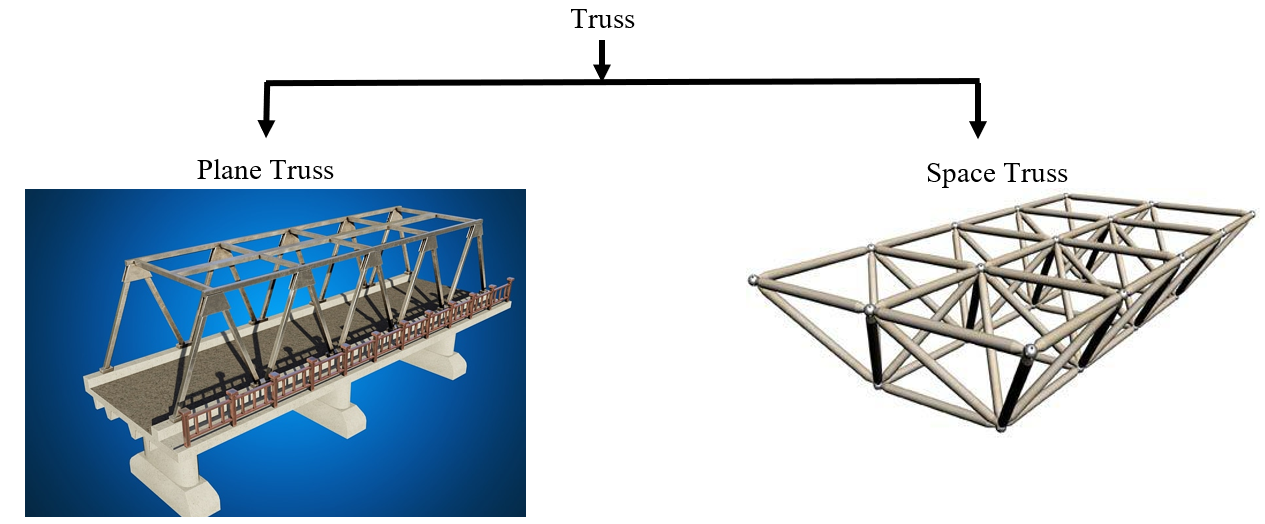
• Plane Truss: A plane truss is a type of truss in which all its members lie in a single plane. This means that all the bars and joints of the truss are confined to a two-dimensional surface. Plane trusses are commonly used for simple and relatively flat structures, such as roof trusses or bridge decks, where the loads and forces primarily act in one plane.
• Space Truss: A space truss is a type of truss in which its members extend into three dimensions and are not confined to a single plane. The bars and joints in a space truss form a three-dimensional network, providing additional stability and load-carrying capacity compared to plane trusses.

Note: Space trusses are generally not included in the syllabus of competitive exams. Therefore, we won't be covering the space truss in detail, as it is not relevant for exam preparation.

Types of Plane Trusses

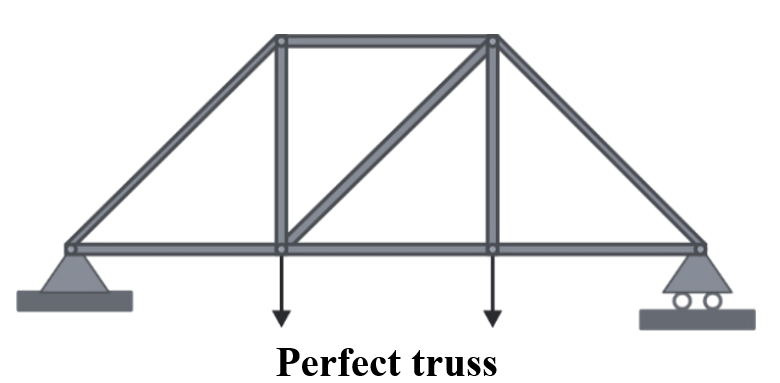
Perfect Truss: -

• A perfect truss is one composed of just sufficient members to maintain equilibrium when subjected to loads without experiencing any deformation in its shape.
• A perfect truss is statically determinate.

m → number of members, j → number of joints, r → number of reactions

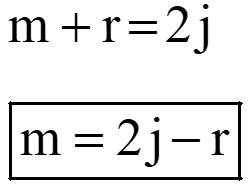
Imperfect Truss

A truss is called imperfect truss when the actual number of members in truss is more or less than the minimum number of members required for perfect truss. (i.e., m≠ 2j-r )

• A truss is called imperfect deficient truss or deficient truss when the actual number of members in truss is less than the minimum number of members required for perfect truss. (i.e., m < 2j-r )
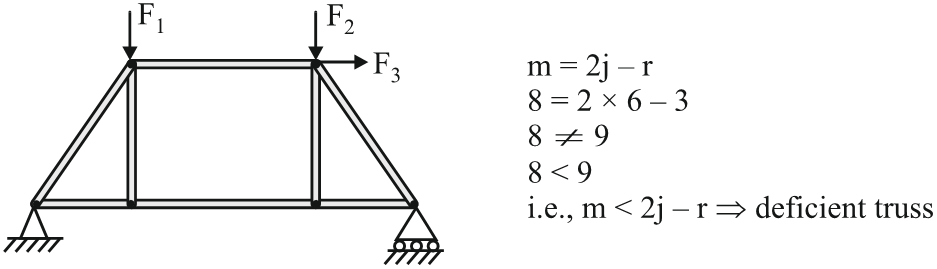
• A truss is called imperfect redundant truss or redundant truss when the actual number of members in truss is more than the minimum number of members required for perfect truss. (i.e., m > 2j-r )

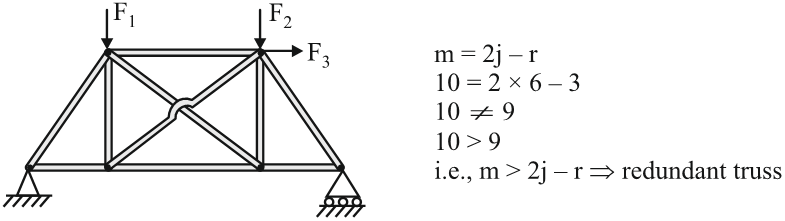
Note: When the support conditions are idealized (e.g., one hinge support and one roller support), the number of unknown reactions will be three, and the expression for a

• perfect truss will be as follows: m = 2j − 3
• deficient truss will be as follows: m < 2j − 3
• redundant truss will be as follows: m > 2j − 3