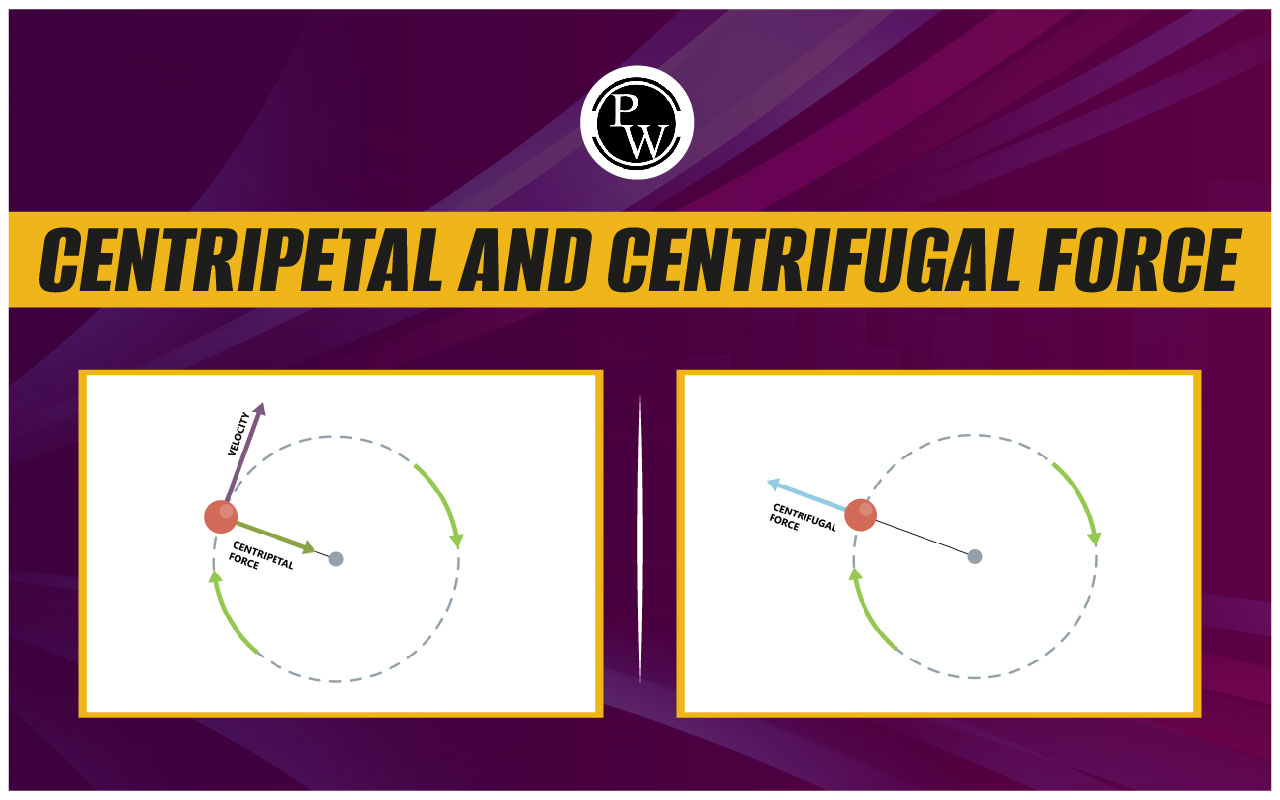
Centripetal and Centrigugal force :
Circular motion is a two-dimensional motion or motion in a plane. This plane may be horizontal, inclined or vertical. But in most cases, this plane is horizontal. In circular motion, direction of velocity continuously keeps on changing. Therefore, even though speed is constant, and velocity keeps on changing. So, body is accelerated. Later the concept of centripetal and centrifugal or coriolis
f
force is introduced with conceptual understanding followed by formulation.
Centripetal Force
Centripetal Force :
In linear acceleration of a particle in circular motion has two components, tangential and radial (or centripetal). So, normally we resolve the forces acting on the particle in two directions:
(i)
Tangential
(ii)
Radial
In tangential direction, the net force on the particle is
ma
t
and in radial direction net force is
ma
r
. In uniform circular motion, tangential acceleration is zero. Hence, net force in tangential direction is zero and in radial direction. Centripetal force given by
mr
ω
2
(towards center) does not act on the particle but this much force is required to the particle for rotating in a circle (as it is accelerated due to change in direction of velocity).
The real forces acting on the particle provide this centripetal force, or we can say that vector sum of all the forces acting on the particle is equal to
mr
ω
2
(in case of uniform circular motion). The real forces acting.
on the particle may be, friction force, weight, normal reaction, tension etc.
Centrifugal Force
Centrifugal Force :
Newton’s laws are valid only in inertial frames. In non-inertial frames a pseudo force −
ma
has to be applied. (
a
= acceleration of frame of reference). After applying the pseudo force one can apply. Newton’s laws in their usual form. Now, suppose a frame of reference is rotating with constant angular velocity ω in a circle of radius ‘
r
’. Then, it will become a non-inertial frame of acceleration
r
ω
2
towards the center.
Now, if we observe an object of mass ‘m’ from this frame then a pseudo force of magnitude mrω2 will have to be applied to this object in a direction away from the center. This pseudo force is called the centrifugal force.
Let us understand this by the following example: Suppose the observer is sitting in a closed cabin which is made to rotate about the vertical Z-axis at a uniform angular velocity. The X and Y axes are fixed in the cabin. Consider a heavy box of mass m kept on the floor at a distance r from the Z-axis. Suppose the floor and the box are rough and the box does not slip on the floor as the cabin rotates.
The box is at rest with respect to the cabin and hence is rotating with respect to the ground at an angular velocity. Let us first analyze the motion of the box from the ground frame. In this frame (which is inertial) the box is moving in a circle of radius r. It, therefore, has an acceleration
v
2
/
r
towards the center. The resultant force on the box must be towards the center and its magnitude must be
m
2
r
. The forces on the box are (
a
) weight mg (
b
) normal force N by the floor (
c
) friction f by the floor.
Figure shows the free body diagram for the box. The resultant is towards the center and its magnitude is
mv
2
/
r
. The floor exerts a force of static friction
f
=
mv
2
/
r
towards the origin. Now consider the same box when observed from the frame of the rotating cabin. The observer there finds that the box is at rest. If he or she applies Newton’s laws, the resultant force on the box should be zero.
The weight and the normal contact force balance each other but the frictional force
f
=
mv
2
/
r
acts on the box towards the origin. To make the resultant zero, a pseudo force must be assumed which acts on the box away from the center (radially outward) and has a magnitude
m
2
r
. This pseudo force is called the centrifugal force. The analysis from the rotating frame is as follows: The forces on the box are (a) weight mg (b) normal force N (c) friction f (d) centrifugal force
mv
2
/
r
.
Note that we get the same equation for friction as we got from the ground frame. But we had to apply Newton’s second law from the ground frame and Newton’s first law from the rotating frame. Let us now summarize our discussion. Suppose we are working from a frame of reference that is rotating at a constant angular velocity with respect to an inertial frame.
If we analyse the dynamics of a particle of mass m kept at a distance
r
from the axis of rotation, we have to assume that a force
mv
2
/
r
acts radially outward on the particle. Only then we can apply Newton’s laws of motion in the rotating frame. This radially outward pseudo force is called the centrifugal force.
In fact, centrifugal force is a sufficient pseudo force, only if we are analysing the particles at rest in a uniformly rotating frame. If we analyse the motion of a particle that moves in the rotating frame, we may have to assume other pseudo forces, together with the centrifugal force. Such forces are called the coriolis forces. The coriolis force is perpendicular to the velocity of the particle and also perpendicular to the axis of rotation of the frame. Once again, we emphasize that all these pseudo forces, centrifugal or coriolis, are needed only if the working frame is rotating. If we work from an inertial frame, there is no need to apply any pseudo force.
