Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Rotational Motion: Definition, Formulas, and Applications
Q.1: What is the difference between rotational motion and linear motion?
Ans. Rotational motion involves the movement of an object around a fixed axis, while linear motion involves movement in a straight line. In rotational motion, objects spin around a central point, whereas in linear motion, objects move from one point to another in a straight path.
Q.2: What are some real-world examples of rotational motion?
Ans. Examples of rotational motion include the rotation of wheels on a vehicle, the spinning of a ceiling fan, the turning of a steering wheel, and the rotation of planets and stars in space.
Q.3: How is angular velocity different from linear velocity?
Ans. Angular velocity measures the rate of change of angular displacement, while linear velocity measures the rate of change of linear displacement. Angular velocity is expressed in radians per second (rad/s), while linear velocity is typically expressed in meters per second (m/s).
Q.4: What is the significance of moment of inertia in rotational motion?
Ans. The moment of inertia quantifies an object's resistance to changes in its rotational motion. It depends on both the mass and distribution of mass within the object. Objects with a higher moment of inertia require more torque to change their rotational motion.
Q.5: How does torque affect rotational motion?
Ans. Torque is the rotational equivalent of force and is responsible for causing an object to rotate around its axis. It is determined by the product of the applied force and the lever arm (distance from the axis of rotation). Torque is essential for changing the angular momentum of an object.
Rotational Motion In JEE Physics Syllabus 2024, Definition, Formulas, Key Concepts And Applications
Rotational motion : Understanding rotational motion is essential in a wide range of scientific and engineering disciplines. Whether it's designing efficient machinery or explaining celestial phenomena, the principles of rotational motion are pervasive in our world.
Srinjoy Pan22 Nov, 2023
Share
Introduction To Rotational Motion:
Rotational motion, also known as angular motion, is a fundamental concept in physics that describes the movement of an object around a fixed axis. Unlike linear motion, where an object moves in a straight line, rotational motion involves the rotation of an object around a central point or axis.
This type of motion is prevalent in both the natural world and in man-made systems. From the spinning of celestial bodies like planets and stars to the rotation of wheels in vehicles, understanding and analyzing rotational motion is crucial in various scientific, engineering, and everyday contexts.
Key Characteristics Of Rotational Motion
Axis of Rotation
At the heart of rotational motion lies the concept of an axis. This imaginary line serves as the center around which an object rotates. The behavior of rotational motion is often analyzed with respect to this fixed axis.
Circular Motion
Rotational motion is intimately connected with circular motion. Objects undergoing rotational motion trace out circular paths, which is why concepts like radius and circumference are integral to understanding this phenomenon.
Angular Measurements
Angular measurements, typically expressed in radians, are used to quantify the extent of rotation an object undergoes. These measurements provide a standardized way to describe the change in orientation of an object in rotational motion.
Practical Significance of Rotational Motion
The study of rotational motion has far-reaching implications in various fields of science and engineering. It forms the foundation for understanding complex mechanical systems, celestial mechanics, and the behavior of particles in quantum physics.
From the operation of engines and turbines to the dynamics of celestial bodies in space, the principles of rotational motion are vital in the design, analysis, and optimization of a wide array of technologies and systems.
Exploring Rotational Motion Further
In this comprehensive guide, we will delve into the key concepts, formulas, and applications of rotational motion. Whether you're a student of physics seeking to grasp the fundamental principles or an engineer looking to apply these concepts in practical scenarios, this guide will serve as a valuable resource.
Let's embark on a journey to unravel the intricacies of rotational motion and discover how it shapes the world around us.
Angular displacement refers to the change in angle of an object as it rotates around a fixed point or axis. It is a measure of how far an object has rotated from its initial position. Angular displacement is typically measured in radians, providing a standardized unit to quantify the extent of rotation.
In practical terms, angular displacement can be visualized as the distance traveled along the circumference of a circle during rotation. It is a fundamental concept in rotational motion analysis and serves as the basis for understanding other related parameters.
Angular velocity is a crucial parameter in rotational motion. It quantifies the rate at which an object undergoes angular displacement over time. In other words, it represents how quickly an object is rotating. Angular velocity is measured in radians per second (rad/s).
Analogous to linear velocity, which measures how fast an object is moving in a straight line, angular velocity provides insight into the rotational speed of an object around its axis. Understanding angular velocity is essential in various applications, from designing machinery to analyzing celestial bodies' rotational behavior.
Angular acceleration
describes the rate of change of angular velocity with respect to time. It signifies how quickly an object's rotation is changing. Angular acceleration is measured in radians per second squared (rad/s²).
Objects in rotational motion can undergo changes in their rate of rotation, either accelerating or decelerating. Angular acceleration is a crucial parameter in analyzing these changes and is fundamental in understanding the dynamics of rotating systems.
The moment of inertia is a property that quantifies an object's resistance to changes in its rotational motion. It depends not only on the mass of the object but also on how that mass is distributed relative to the axis of rotation.
Objects with a higher moment of inertia are more resistant to changes in their rotational motion, requiring more torque to accelerate or decelerate. Understanding moment of inertia is crucial in engineering applications, especially in the design of machinery and mechanical systems.
Torque
Torque is the rotational equivalent of force in linear motion. It is the product of the force applied to an object and the distance from the axis of rotation at which the force is applied. Torque is measured in Newton-meters (N·m) or foot-pounds (ft·lb).
In practical terms, torque is what causes an object to rotate around its axis. It plays a central role in various mechanical systems, from engines and transmissions in vehicles to the operation of machinery in manufacturing processes.
Angular displacement represents the change in angle as an object rotates around a fixed axis. It is defined as the ratio of the arc length traveled along the circumference of the circle to the radius from the axis of rotation:
Where:
θ is the angular displacement in radians.
s
is the arc length along the circumference.
r
is the radius from the axis of rotation.
This formula provides a straightforward way to quantify the extent of rotation an object undergoes.
Angular velocity measures the rate of change of angular displacement with respect to time. It is calculated as the change in angular displacement divided by the change in time: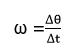
Where:
ω
is the angular velocity in radians per second.
is the change in angular displacement.
Δ
t
is the change in time.
Angular velocity provides crucial information about how quickly an object is rotating.
Angular acceleration quantifies the rate of change of angular velocity. It is determined by dividing the change in angular velocity by the change in time:
Where:
α
is the angular acceleration in radians per second squared.
Δ
ω
is the change in angular velocity.
Δ
t
is the change in time.
Angular acceleration is essential for understanding how an object's rotation is changing over time.
The moment of inertia is a property that characterizes an object's resistance to changes in its rotational motion. It is calculated through integration, summing up the contributions of all mass elements within the object:
I=∫
r
2
dm
Where:
I
is the moment of inertia.
r
is the distance from the axis of rotation.
dm
is the mass element.
Moment of inertia plays a crucial role in engineering applications, especially in designing mechanical systems.
Torque is the rotational equivalent of force. It is calculated as the product of the applied force and the lever arm (distance from the axis of rotation) at which the force is applied:
τ
=
rF
sin(θ)
Where:
τ
is the torque.
r
is the distance from the axis of rotation.
F
is the applied force.
θ is the angle between
r
and
F
.
Torque is what causes an object to rotate and is a fundamental concept in mechanical systems.
Rotational motion is a fundamental concept with diverse applications across various scientific, engineering, and everyday contexts. Understanding and harnessing the principles of rotational motion is crucial in the development and operation of numerous technologies and systems. Below are some of the key areas where rotational motion plays a pivotal role:
1. Automotive Engineering
In the automotive industry, rotational motion is at the core of various critical components and systems. Engines, for example, rely on the controlled combustion of fuel to generate rotational motion, which is then transmitted to the wheels via a complex system of gears and axles. Understanding the dynamics of rotational motion is essential for optimizing engine performance, transmission systems, and overall vehicle efficiency.
2.Manufacturing and Machinery
Rotational motion is prevalent in manufacturing processes and machinery operations. Equipment such as lathes, drills, mills, and conveyor systems heavily rely on rotating components to perform tasks like cutting, shaping, and transporting materials. Efficient utilization of rotational motion is crucial in achieving precision and productivity in manufacturing operations.
3.Sports and Athletic Performance
Many sports involve the manipulation of rotational motion for performance. Activities like gymnastics, figure skating, and diving require athletes to control their body's rotation in complex ways. Understanding the principles of rotational motion is vital for athletes to achieve precision, balance, and skill in their movements.
4. Astronomy and Celestial Mechanics
The study of celestial bodies, including planets, stars, and galaxies, relies on a deep understanding of rotational motion. Observing and analyzing the rotation of celestial objects provides insights into their composition, structure, and behavior. Additionally, the rotational dynamics of celestial bodies play a crucial role in astrophysical theories and models.
5.Engineering Design and Machinery
Engineers leverage the principles of rotational motion in designing a wide range of mechanical components and systems. Gears, pulleys, flywheels, and other mechanisms are meticulously engineered to transmit and manipulate rotational motion. Accurate calculations of parameters like moment of inertia and torque are essential for ensuring the functionality and reliability of these components.
6.Physics and Research
Rotational motion is a cornerstone of many areas of physics, including classical mechanics, quantum mechanics, and fluid dynamics. Researchers use the principles of rotational motion to study phenomena ranging from the behavior of subatomic particles to the dynamics of fluid flows. Understanding rotational motion is essential in advancing scientific knowledge across multiple disciplines.
7.Gyroscopic Systems
Gyroscopes, which rely on the principles of rotational motion, are critical components in navigation systems, aerospace technology, and stabilizing devices. They provide stability and maintain orientation in applications such as aircraft navigation, satellite control, and inertial navigation systems.
These applications represent just a subset of the extensive reach of rotational motion in our modern world. From powering engines to guiding spacecraft, from enhancing athletic performance to advancing scientific research, the principles of rotational motion continue to shape and revolutionize various fields of science and engineering.
Where:
Where:
Where:
