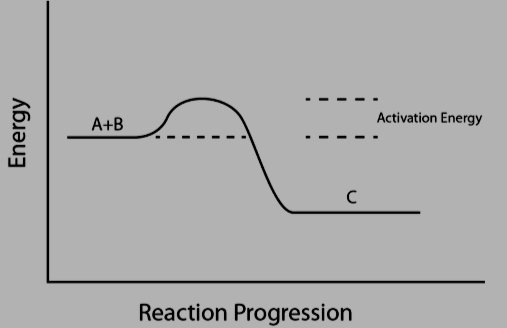
Activation Energy Formula: The activation energy of a chemical reaction represents the minimum energy required to initiate the reaction. It can be thought of as the energy difference between the initial state of molecules and atoms and the activated or transition state configuration required for the reaction to proceed. To kickstart a reaction, molecules must collide with sufficient kinetic energy, exchanging energy and velocity. Without this collision or adequate kinetic energy, the reaction will not occur. This concept is quantified in kilojoules per mole (kJ/mol).
Also Check –
Theoretical Yield Formula
Activation Energy Formula
The activation energy (Ea) can be determine using the Arrhenius equation:
Ea = 2.303 * R * (log(k2/k1)) * (T1 * T2) / (T2 - T1)
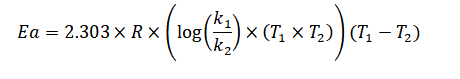
Where:
Ea is the activation energy.
R is the ideal gas constant (8.3145 J/K mol).
k1 and k2 are the rate constants at initial and final temperatures.
T1 is the initial temperature.
T2 is the final temperature.
Derivation:
Let's consider a reaction between reactants P and Q yielding product R, with a rate constant denoted as k.
The formula for the rate constant is as follows:
ln(k) = -Ea / (RT) + ln(A)
For the initial temperature T1 and rate constant k1, we have:
ln(k1) = -Ea / (R * T1) + ln(A) ... (1)
For the final temperature T2 and rate constant k2, we have:
ln(k2) = -Ea / (R * T2) + ln(A) ... (2)
Subtracting (2) from (1), we obtain:
ln(k2/k1) = Ea * (1/T1 - 1/T2) * R
2.303 * log(k2/k1) = Ea * (1/T1 - 1/T2) * R
Also Check –
Vapor Pressure Formula
Activation Energy Formula Solved Examples
Example 1:
A chemical reaction has a rate that increases sevenfold when the temperature is raised from 25°C to 75°C. Calculate the activation energy for this reaction.
Solution:
Given: T1 = 25°C = 298 K, T2 = 75°C = 348 K, and k2 = 7 * k1.
Using the formula:
Ea = 2.303 * R * (log(7)) * (298 * 348) / (348 - 298)
Ea ≈ 24.77 kJ/mol
Example 2:
In a certain reaction, the rate is halved when the temperature is reduced from 400 K to 300 K. Calculate the activation energy for this reaction.
Solution:
Given: T1 = 400 K, T2 = 300 K, and k2 = 0.5 * k1.
Using the formula:
Ea = 2.303 * R * (log(0.5)) * (400 * 300) / (300 - 400)
Ea ≈ 56.56 kJ/mol
Also Check –
Tungstic Acid Formula
Example 3:
For a chemical reaction, the rate constant triples when the temperature changes from 273 K to 373 K. Calculate the activation energy for this reaction.
Solution:
Given: T1 = 273 K, T2 = 373 K, and k2 = 3 * k1.
Using the formula:
Ea = 2.303 * R * (log(3)) * (273 * 373) / (373 - 273)
Ea ≈ 61.02 kJ/mol
Example 4:
In an enzyme-catalyzed reaction, the rate increases by a factor of 4 when the temperature is increased from 25°C to 37°C. Calculate the activation energy for this enzymatic reaction.
Solution:
Given: T1 = 25°C = 298 K, T2 = 37°C = 310 K, and k2 = 4 * k1.
Using the formula:
Ea = 2.303 * R * (log(4)) * (298 * 310) / (310 - 298)
Ea ≈ 22.40 kJ/mol
Also Check –
Empirical Formula
Example 5:
For a chemical reaction, the rate constant is observed to increase fivefold when the temperature changes from 200 K to 250 K. Calculate the activation energy for this reaction.
Solution:
Given: T1 = 200 K, T2 = 250 K, and k2 = 5 * k1.
Using the formula:
Ea = 2.303 * R * (log(5)) * (200 * 250) / (250 - 200)
Ea ≈ 31.62 kJ/mol
Example 6
: In a chemical reaction, the rate constant is found to increase by a factor of 2 when the temperature is raised from 300 K to 350 K. Calculate the activation energy for this reaction.
Solution:
Given: T1 = 300 K, T2 = 350 K, and k2 = 2 * k1.
Using the Arrhenius equation:
Ea = 2.303 * R * (log(2)) * (300 * 350) / (350 - 300)
Ea ≈ 20.96 kJ/mol
So, the activation energy for this reaction is approximately 20.96 kJ/mol.
These examples demonstrate the application of the Arrhenius equation to determine the activation energy of various chemical reactions based on changes in temperature and rate constants.
