CBSE Class 6 Maths Notes Chapter 10 Mensuration PDF Download
CBSE Class 6 Maths Notes Chapter 10 Mensuration is provided here. Students can use our CBSE Class 6 Maths Notes Chapter 10 and prepare better for their examinations.
Neha Tanna20 Sept, 2024
Share
CBSE Class 6 Maths Notes Chapter 10: The idea of measuring the size of forms and things is introduced in Mensuration, Chapter 10 of CBSE Class 6 Maths. Its main emphasis is on area and perimeter calculations. The perimeter of a closed figure, like a rectangle, square, or triangle, is its entire boundary length.
The perimeter of a rectangle is equal to 2 × (length plus breadth), and the perimeter of a square is equal to 4 × side. The area, or the space encircled by a shape, is also covered in this chapter. Area is calculated as length × width for a rectangle and as side × side for a square. These ideas are reinforced by real-world examples.CBSE Class 6 Maths Notes Chapter 10 Overview
Students should read Chapter 10 of CBSE Class 6 Maths, Mensuration, as it presents fundamental ideas of measuring that are important in daily life. Through the process of calculating the area and perimeter of forms such as triangles, squares, and rectangles, students get a fundamental understanding of spatial dimensions. This chapter provides practical applications, like measuring a room's space or building a garden fence, to promote logical thinking. Comprehending these ideas aids in the development of students' problem-solving abilities, which facilitates their understanding of more complex material in upper-level classes. Furthermore, future applications in geometry, physics, and engineering are built around the capacity to compute perimeter and area. This chapter's practical approach guarantees that students may use what they have learnt in a variety of everyday circumstances outside of the classroom.CBSE Class 6 Maths Notes Chapter 10 PDF
Below we have provided CBSE Class 6 Maths Notes Chapter 10 Mensuration for the ease of the students. Students can download this CBSE Class 6 Maths Notes Chapter 10 Mensuration pdf from the below link and access it without internet.CBSE Class 6 Maths Notes Chapter 10 PDF
CBSE Class 6 Maths Notes Chapter 10 Mensuration
Below is CBSE Class 6 Maths Notes Chapter 10 Mensuration - One area of mathematics that is covered in geometry is mensuration. It is the study of different geometric shapes, including 2D and 3D shapes, including their length, breadth, volume, and area. The terms that are relevant to this topic are discussed below.Introduction to Mensuration
Mensuration
Mensuration is the branch of mathematics that deals with the measurement of various geometric shapes' lengths, areas, and volumes.Shapes
An object's form is its shape. The shapes square, rectangle, and triangle are examples of two-dimensional shapes; cube, cuboid, and sphere are examples of three-dimensional shapes.Perimeter
- Perimeter is the total length or total distance covered along the boundary of a closed shape.
- Perimeter of a circle is also called as the circumference of the circle.
Perimeter of a Triangle
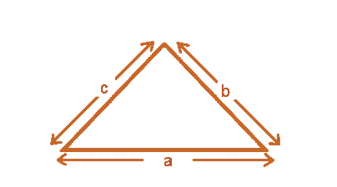
- Perimeter of triangle = Sum of lengths of all sides = a + b + c.
- If the given triangle is equilateral that is if all the sides are equal (a = b = c), then its perimeter is equal to 3 × length of one side of the triangle.
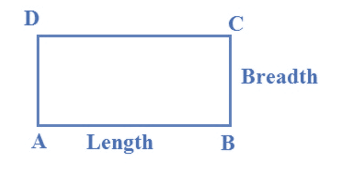
Perimeter of a Rectangle
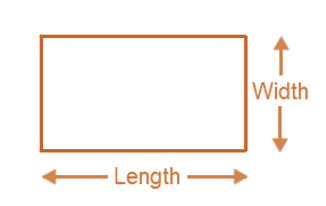
- Perimeter of the rectangle = length ( l ) + length ( l ) + width (w) + width (w)
Perimeter of a Square
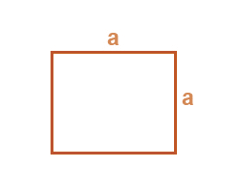Perimeter of square = 4 × length of a side = 4a
Perimeter of an ‘n’ Sided Polygon
A closed shape composed of line segments is called a polygon. n× length of one side equals the perimeter of an n-sided polygon. For instance: If a hexagon's side lengths are each one centimetre, then: Hexagonal perimeter = 6 a cm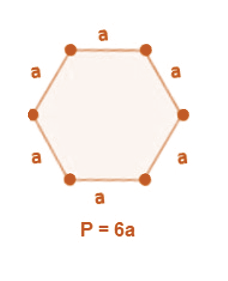
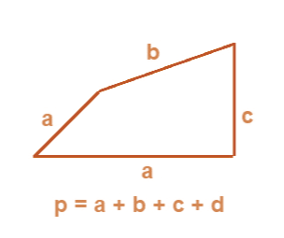
Perimeter of Irregular Sshapes
Shapes classified as irregular have non-equal angles and sides. The entire length that an irregular form covers is its perimeter. The perimeter of the following figure is equal to the sum of its sides.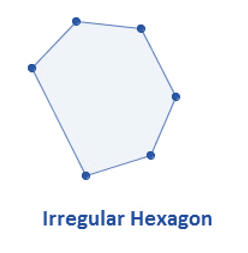
Area
- Area is the total amount of surface enclosed by a closed figure.
Area of Square
- Area of a square = Side × Side =Side 2 =a 2 , where a is the length of each side.
Area of Rectangle
- Area = length ( l ) × breadth ( b)
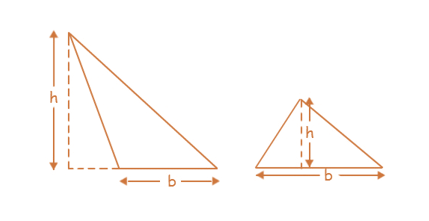
Area of Triangle
Area of triangle = (1/2) × base × height = (1/2) × b × h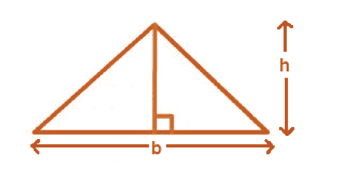
Areas of different types of triangles
- Consider an acute and an obtuse triangle. Area of each triangle = (1/2) × base × height = (1/2) × b × h
Visualisation of Area
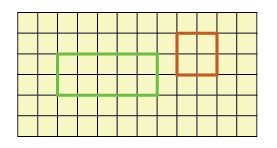
- In the given graph, if the area of each small square is 1 cm 2 , then Area of rectangle = l×b = 5×2 = 10cm 2 Area of square = a×a = 2×2 =4cm 2
Area of Irregular Shapes
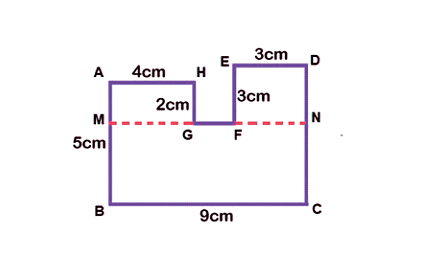
An irregular figure's area can be computed: Step 1: Split the irregular shape into easily recognisable regular shapes (such as squares, rectangles, triangles, and circles). Step 2: Add these individual shapes to the region you found. The area of the irregular figure will be the sum.- Example: Area of the given figure = Area of MNCB + Area of AMGH + Area of EFND = [ 5 × 9 + 4 × 2 + 3 × 3 ] cm 2 = [45 + 8 + 9 ] cm 2 =62 cm 2
Benefits of CBSE Class 6 Maths Notes Chapter 10
The benefits of studying Chapter 10, Mensuration , in CBSE Class 6 Maths include:Foundation for Geometry : It provides the groundwork for understanding key geometric concepts such as perimeter and area, which are essential for higher-level mathematics.
Practical Applications : The knowledge gained from this chapter is useful in real-life situations like calculating areas for painting walls, flooring, or measuring land for construction.
Problem-Solving Skills : Students develop analytical and logical thinking by solving practical problems related to measurement.
Improves Spatial Understanding : Helps students visualize and understand the dimensions of various shapes, boosting their spatial awareness.
Future Readiness : The concepts learned are critical for advanced studies in fields like engineering, architecture, and design, making students ready for future academic challenges.
Boosts Accuracy in Measurements : It enhances precision when dealing with measurements, which is important for various practical tasks in everyday life.
CBSE Class 6 Maths Notes Chapter 10 FAQs
What is the purpose of mensuration?
Mensuration is the branch of mathematics that studies the measurement of geometric figures and their parameters like length, volume, shape, surface area, lateral surface area, etc.
What are the basics of mensuration?
Mensuration is a division of mathematics that studies geometric figure calculation and its parameters such as area, length, volume, lateral surface area, surface area, etc. It outlines the principles of calculation and discusses all the essential equations and properties of various geometric shapes and figures.
What are the rules of mensuration?
Mensuration Formulas: Area of rectangle (A) is equal to length(l) × Breath(b) Perimeter of a rectangle (P) is equal to 2 × (Length(l) + Breath(b)) Area of a square (A) is equal to Length (l) × Length (l)
Who is the father of mensuration?
Leonard Digges
Where is mensuration used in real life?
The length of cloth needed for sewing, the size of a wall to be painted, the perimeter of a circular garden to be fenced, and the amount of water needed to fill the tank are some examples of mensuration. Standard and non-standard units of measurement can be used to measure items and amounts.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.