NCERT Solutions for Class 6 Maths Chapter 6 Integers
Jasdeep Bhatia6 Jan, 2024
Share
NCERT Solutions for Class 6 Maths Chapter 6
NCERT Solutions for Class 6 Maths Chapter 6: Chapter 6 of the Class 6 math syllabus focuses on Integers. This essential chapter is divided into four main sections. Below is a list of the key topics covered in NCERT Solutions for Class 6 Math Chapter 6 - Integers. It is suggested that students explore each of the four topics to make the most of PW’s provided solutions for this Integer chapter. These four topics encompass the entire content of the Integer chapter. Students can be confident that understanding these topics will facilitate practicing the given solutions effortlessly and achieving high marks in exams that involve integer-based questions.NCERT Solutions for Class 6 Maths Chapter 6 Overview
The NCERT Solutions for Class 6 Maths Chapter 6 present a brief solution to each topic in this chapter. Following these solutions, along with the textbook, will assist students in enhancing their performance and achieving better results. NCERT Solution for Class 6 Mathematics Chapter 6 delves into the concept of integers. There are four sections with subsections that elaborate on the idea of integers. For additional marks in examinations, you can download NCERT Solution for Class 6 Science. The chapter commences with a specific problem and proceeds to introduce negative numbers. As students advance through the chapter, they encounter new topics such as the representation of integers on a number line, ordering and addition of integers, subtraction of integers, and more.
NCERT Solutions for Class 6 Maths Chapter 6 Integers
NCERT solutions for Chapter 6 of Class 6 Maths serve as important study material for students getting ready for their exams. The solutions clarify the concepts in a simpler way, helping students understand the topics rapidly. This makes it effortless for students to comprehend both the fundamental and more advanced ideas. The solutions are accessible online without any cost, and they can be easily found on different websites. Keep on reading to see the solutions in detail: Exercise 6.1 Page No: 120 1. Write opposites of the following. (a) Increase in weight (b) 30 km north (c) 80 m east (d) Loss of Rs 700 (e) 100 m above sea level Solutions: (a) The opposite of an increase in weight is a decrease in weight. (b) The opposite of 30 km north is 30 km south. (c) The opposite of 80 m east is 80 m west. (d) The opposite of a loss of Rs 700 is a gain of Rs 700. (e) The opposite of 100 m above sea level is 100 m below sea level. 2. Represent the following numbers as integers with appropriate signs. (a) An aeroplane is flying at the height of two thousand meters above the ground. (b) A submarine is moving at a depth of eight hundred meters below sea level. (c) A deposit of rupees two hundred. (d) Withdrawal of rupees seven hundred. Solutions: (a) + 2000 m (b) – 800 m (c) + Rs 200 (d) – Rs 700CBSE Board Exam Centre List 2024
3. Represent the following numbers on a number line.
(a) + 5 (b) – 10 (c) + 8 (d) – 1 (e) – 6 Solutions: (a) + 5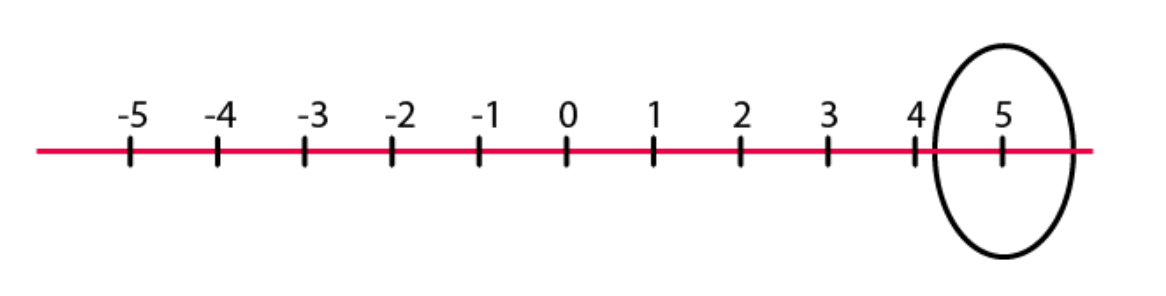
(b)
– 10
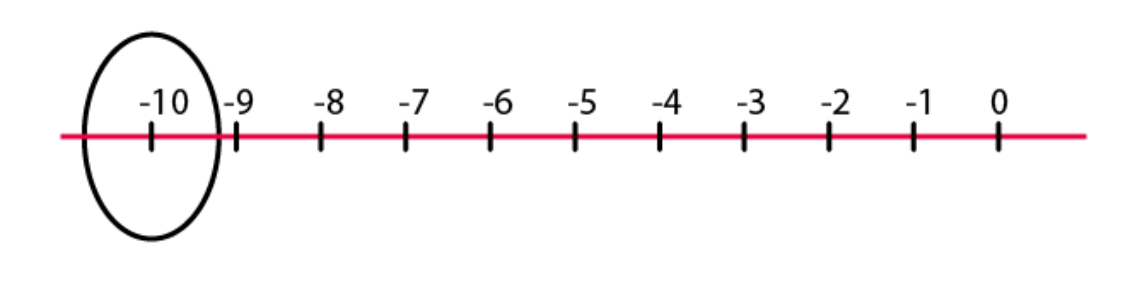(c)
+ 8
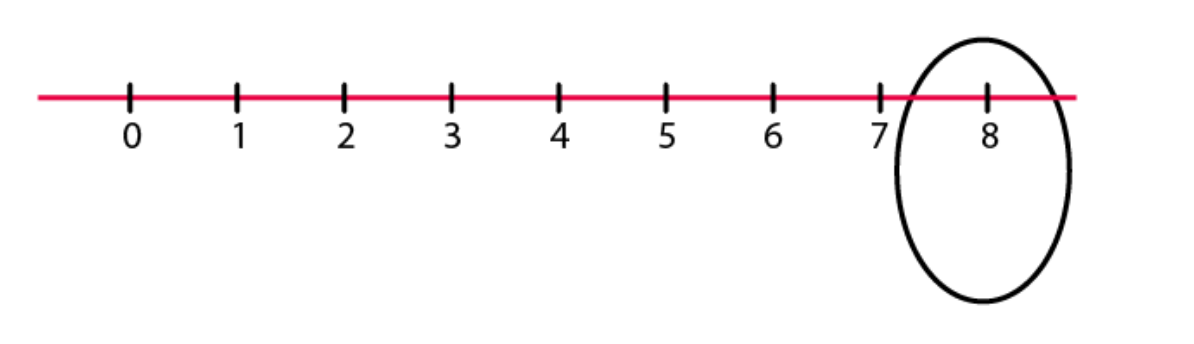(d)
– 1
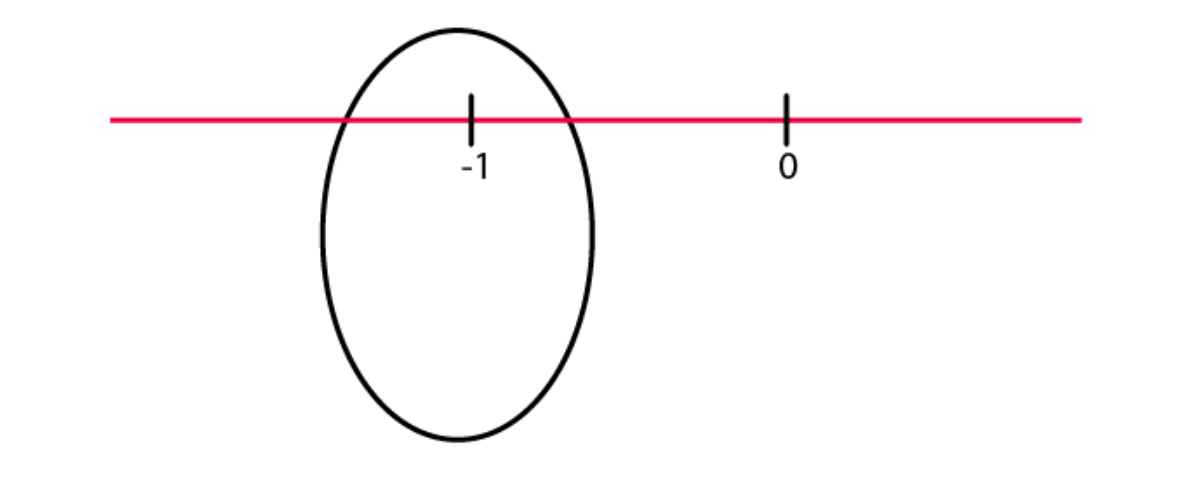(e)
– 6
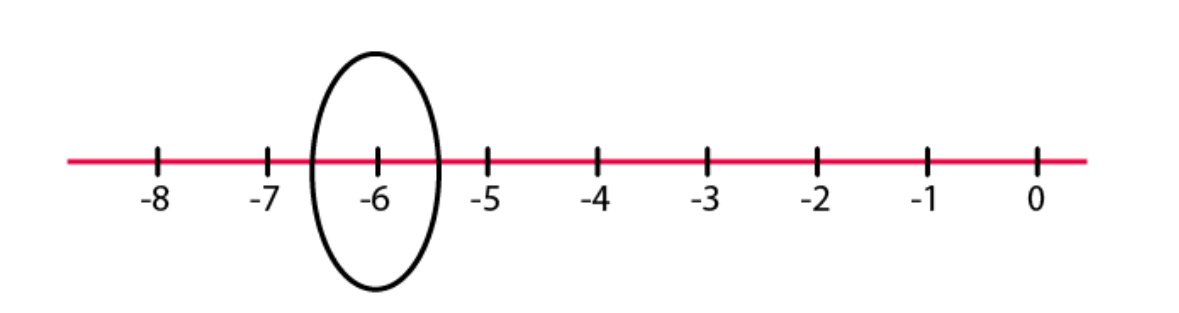4. Adjacent figure is a vertical number line representing integers. Observe it and locate the following points.
(a) If point D is + 8, then which point is – 8?
(b) Is point G a negative integer or a positive integer?
(c) Write integers for points B and E.
(d) Which point marked on this number line has the least value?
(e) Arrange all the points in decreasing order of value.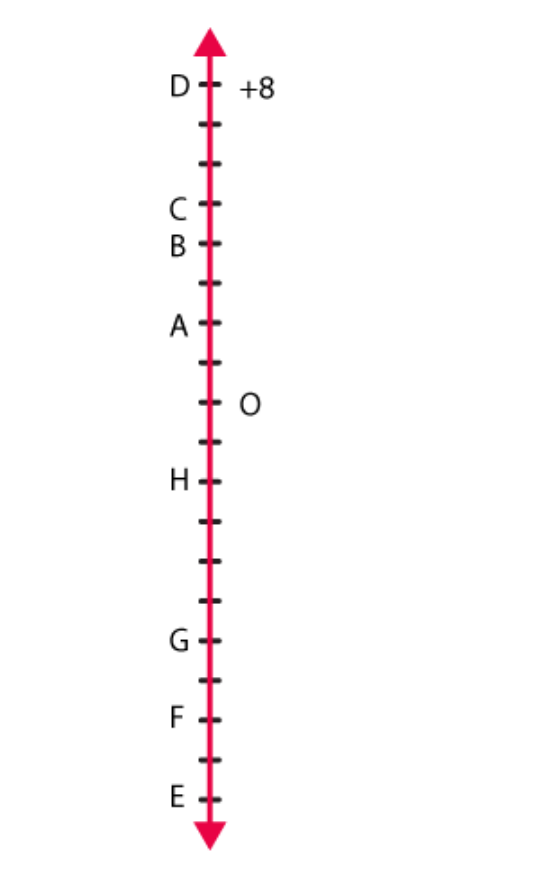
Solutions:
(a)
If point D is +8, then point F is -8.
(b)
Point G is a negative integer.
(c)
Point B is 4, and point E is – 10.
(d)
The least value on this number line is point E, as it represents – 10.
(e)
The points in decreasing order of value are D, C, B, A, O, H, G, F, E.
NCERT Solutions for Class 6 Maths Chapter 2
5. Following is the list of temperatures of five places in India on a particular day of the year.
Place Temperature Siachen 10°C below 0°C …………….. Shimla 2°C below 0°C …………….. Ahmedabad 30°C above 0°C …………….. Delhi 20°C above 0°C …………….. Srinagar 5°C below 0°C …………….. (a) Write the temperatures of these places in the form of integers in the blank column. (b) Following is the number line representing the temperature in degree Celsius. Plot the name of the city against its temperature.
(c) Which is the coolest place?
(d) Write the names of the places where temperatures are above 10°C.
Solutions:
(a)
Siachen – 10 degree
C
Shimla – 2
0
degree C
Ahmedabad + 30
0
degree C
Delhi + 20 degree
C
Srinagar – 5
0 degree
C
(b)
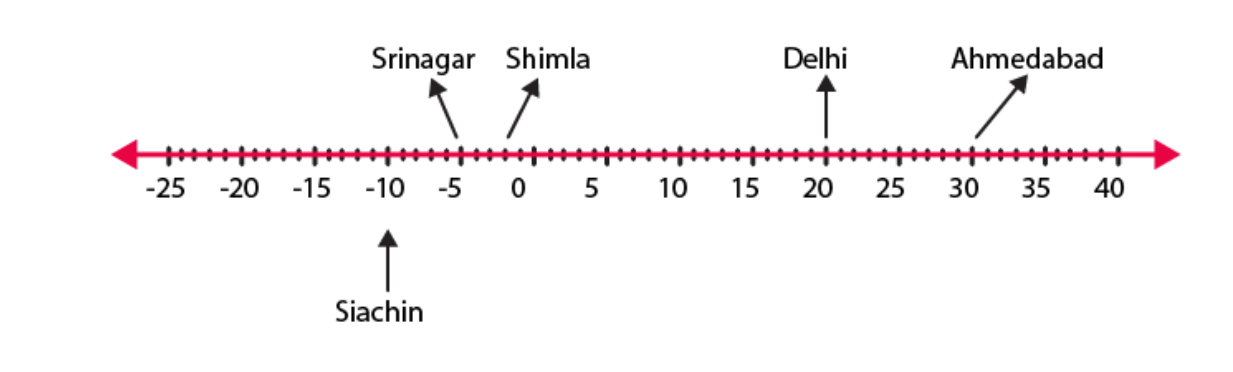
(c) Siachen is the coolest place.
(d) Ahmedabad and Delhi are the places where the temperatures are above 100C.
6. In each of the following pairs, which number is to the right of the other on the number line?
(a) 2, 9
(b) – 3, – 8
(c) 0, – 1
(d) – 11, 10
(e) – 6, 6
(f) 1, – 100
Solutions :
(a) 9 lies to the right on the number line (9 > 2).
(b) – 3 lies to the right on the number line (- 3 > – 8).
(c) 0 lies to the right on the number line (0 > -1).
(d) 10 lies to the right on the number line (10 > -11).
(e) 6 lies to the right on the number line (6 > -6).
(f) 1 lies to the right on the number line (1 > -100).
7. Write all the integers between the given pairs (write them in increasing order).
(a) 0 and – 7
(b) – 4 and 4
(c) – 8 and – 15
(d) – 30 and – 23
Solutions:
(a) -6, -5, -4, -3, -2, -1 are the integers between 0 and -7.
(b) -3, -2, -1, 0, 1, 2, 3 are the integers between -4 and 4.
(c) -14, -13, -12, -11, -10, -9 are the integers between -8 and -15.
(d) -29, -28, -27, -26, -25, -24 are the integers between -30 and -23.
8. (a) Write four negative integers greater than – 20.
(b) Write four integers less than – 10.
Solutions:
(a) -19, -18, -17, -16 are the integers greater than -20.
(b) -11, -12, -13, -14 are the integers less than -10.
9. For the following statements, write True (T) or False (F). If the statement is false, correct the statement.
(a) – 8 is to the right of – 10 on a number line.
(b) – 100 is to the right of – 50 on a number line.
(c) Smallest negative integer is – 1.
(d) – 26 is greater than – 25.
Solutions:
(a) True, as (-8 > -10).
(b) False. (-50 is greater than -100). Hence, -100 lies to the left of -50 on the number line.
(c) False. -1 is the greater negative integer.
(d) False. -26 is smaller than -25.
10. Draw a number line and answer the following.
(a) Which number will we reach if we move 4 numbers to the right of – 2?
(b) Which number will we reach if we move 5 numbers to the left of 1?
(c) If we are at – 8 on the number line, in which direction should we move to reach – 13?
(d) If we are at – 6 on the number line, in which direction should we move to reach – 1?
Solutions :
(a)
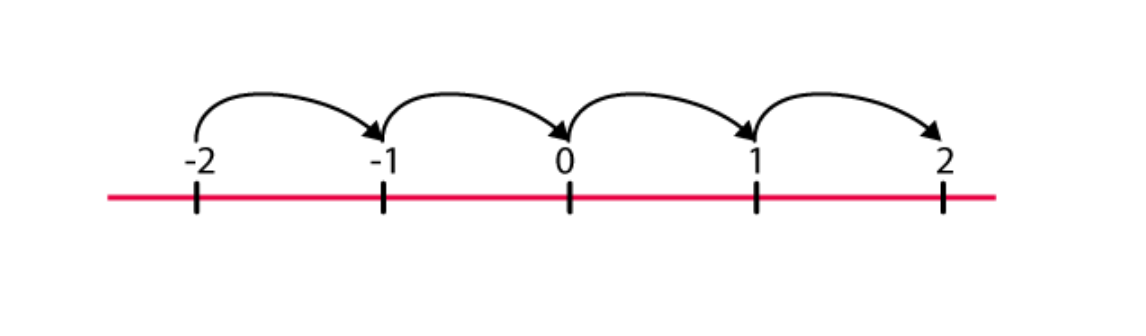If we move 4 numbers to the right of -2, we will reach 2.
(b)
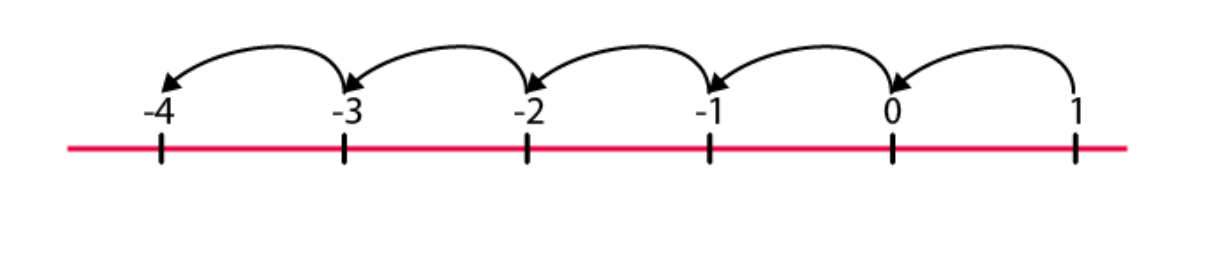If we move 5 numbers to the left of 1, we will reach -4.
(c)
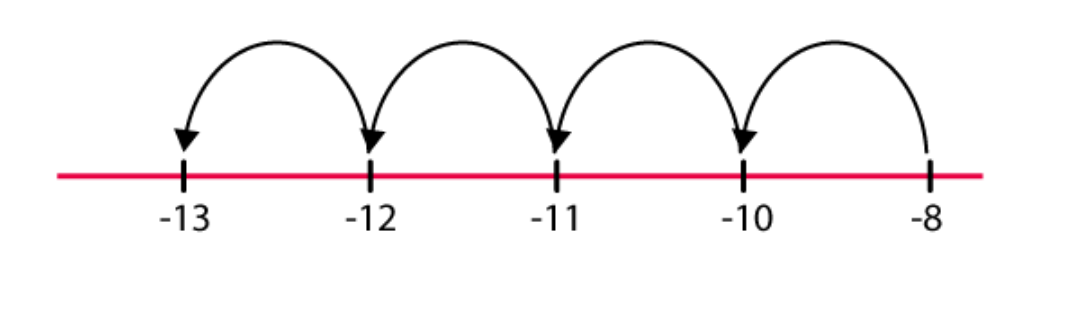-13 lies to the left of -8 on the number line. Hence, we should move towards the left direction.
(d)
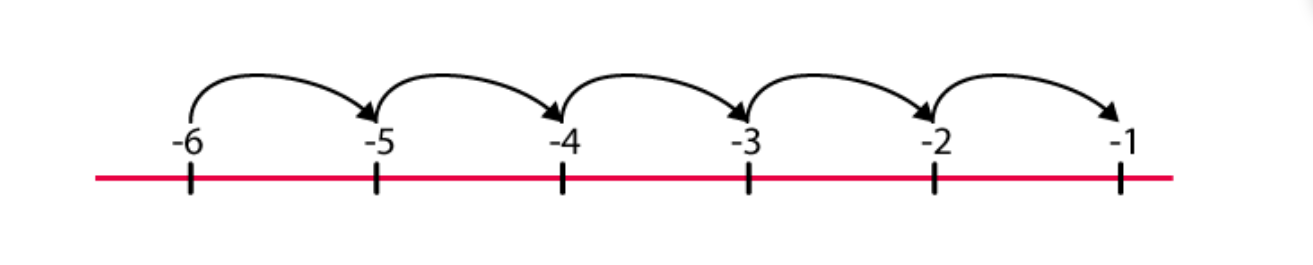-1 lies to the right of -6 on the number line. So, we should move towards the right direction.
| CBSE Syllabus Class 6 | |
| CBSE Class 6 Science Syllabus | CBSE Class 6 Maths Syllabus |
| CBSE Class 6 Social Science Syllabus | CBSE Class 6 English Syllabus |
Exercise 6.2 Page no: 128
1. Using the number line, write the integer which is:
(a) 3 more than 5
(b) 5 more than –5
(c) 6 less than 2
(d) 3 less than –2
Solutions:
(a)
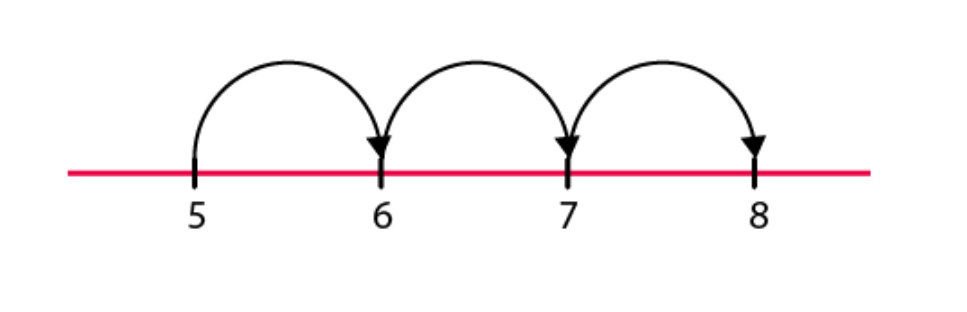Hence, 8
(b)
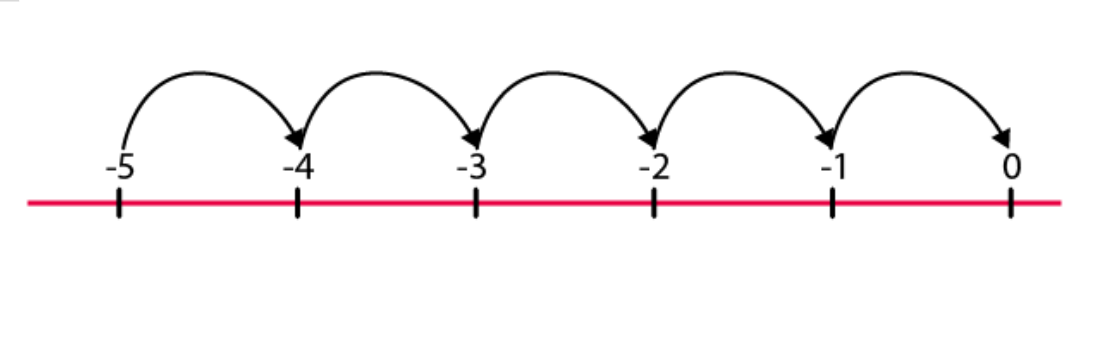Hence, 0
(c)
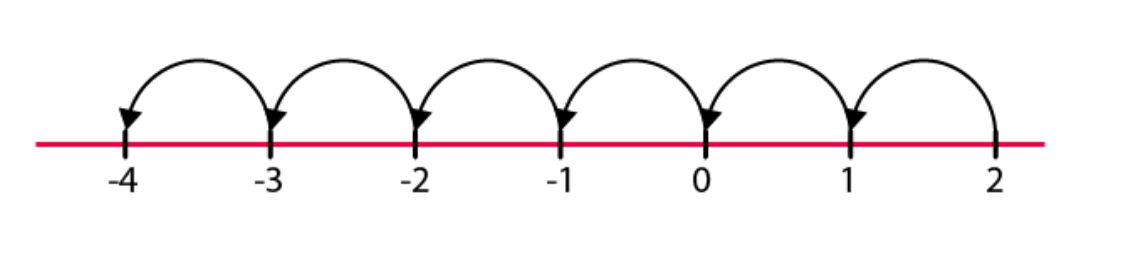Hence, -4
(d)
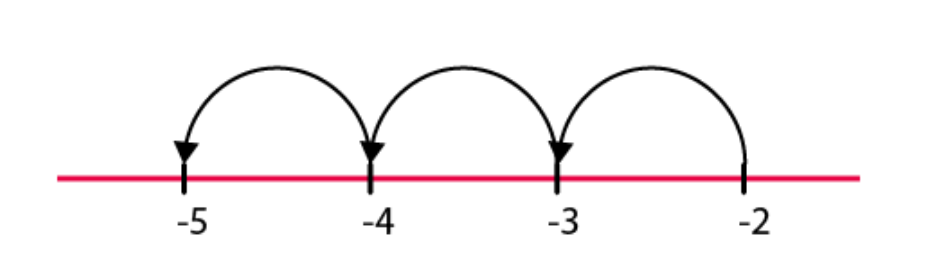Hence, -5
2. Use a number line and add the following integers.
(a) 9 + (–6)
(b) 5 + (–11)
(c) (–1) + (–7)
(d) (–5) + 10
(e) (–1) + (–2) + (–3)
(f) (–2) + 8 + (–4)
Solutions:
(a)
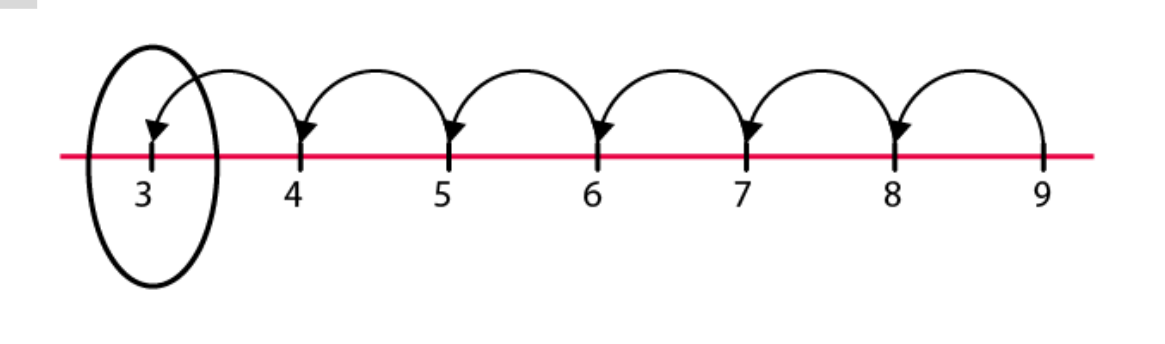Hence, 3
(b)
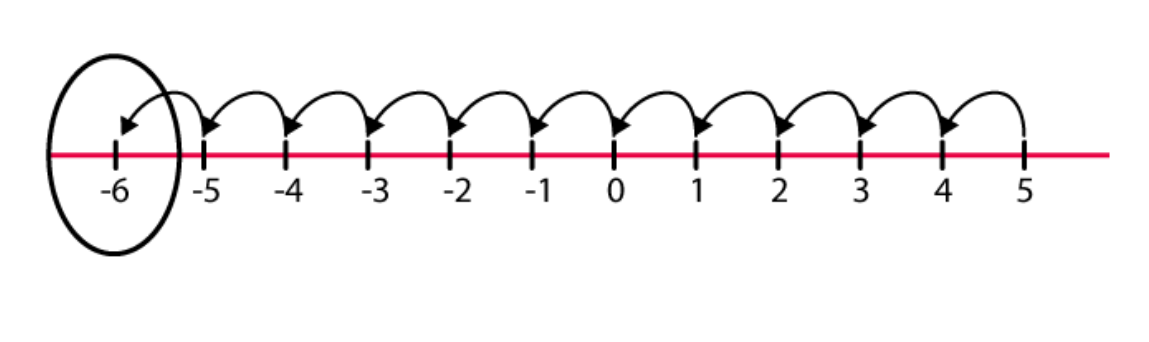Hence, -6
(c)
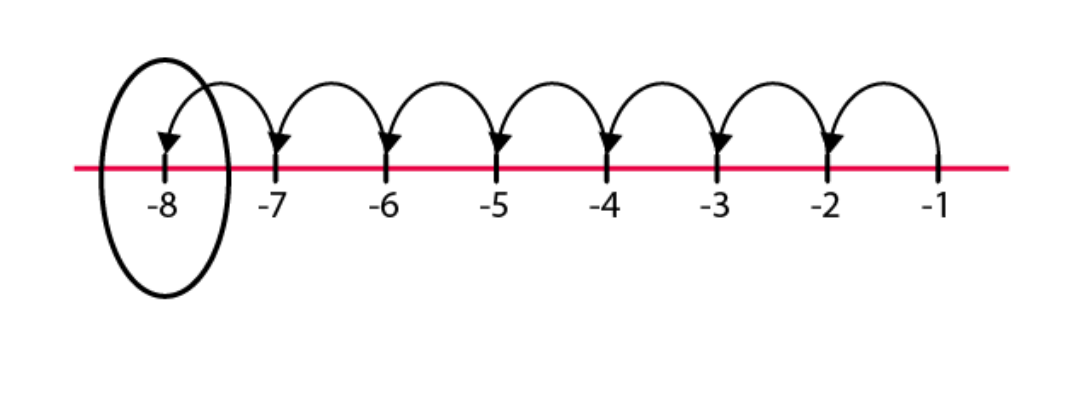Hence, -8
(d)
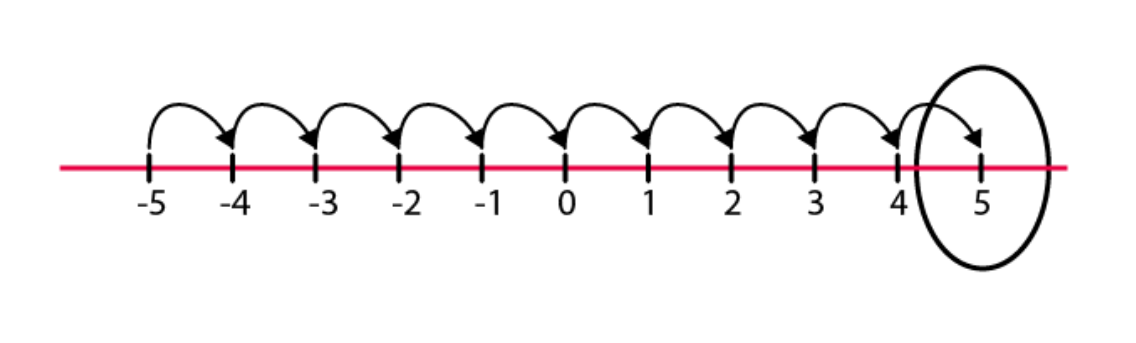Hence, 5
(e)
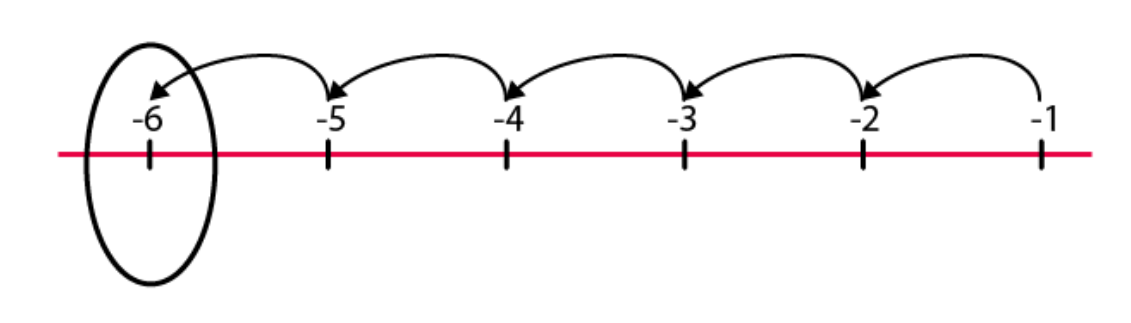Hence, -6
(f)
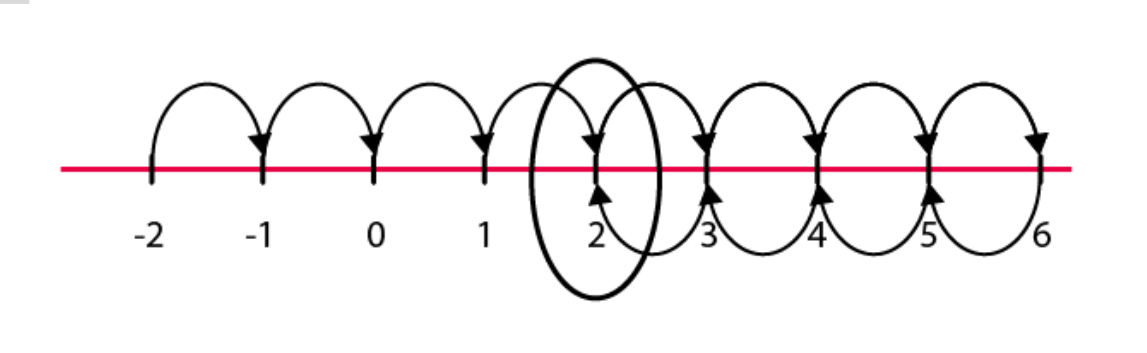Hence, 2
NCERT Solutions for Class 6 Maths Chapter 5
3. Add without using a number line.
(a) 11 + (–7)
(b) (–13) + (+18)
(c) (–10) + (+19)
(d) (–250) + (+150)
(e) (–380) + (–270)
(f) (–217) + (–100)
Solutions:
(a) 11 + (-7) = 4
(b) (-13) + (+18) = 5
(c) (-10) + (+19) = 9
(d) (-250) + (+150) = -100
(e) (-380) + (-270) = -650
(f) (-217) + (-100) = -317
4. Find the sum of:
(a) 137 and – 354
(b) – 52 and 52
(c) – 312, 39 and 192
(d) – 50, – 200 and 300
Solutions:
(a) 137 and -354
(137) + (-354) = (137) + (-137) + (-217) = 0 + (-217) [(137) + (-137) = 0] = (-217) = -217(b) -52 and 52
(-52) + (+52) = 0 [(-a) + (+a) = 0](c) -312, 39 and 192
(-312) + (+39) + (+192) = (-231) + (-81) + (+39) + (+192) = (-231) + (-81) + (+231) = (-231) + (+231) + (-81) = 0 + (-81) [(-a) + (+a) = 0] = -81(d) -50, -200 and 300
(-50) + (-200) + (+300) = (-50) + (-200) + (+200) + (+100) = (-50) + 0 + (+100) [(-a) + (+a) = 0] = (-50) + (+100) = (-50) + (+50) + (+50) = 0 + (+50) [(-a) + (+a) = 0] = 505. Find the sum.
(a) (–7) + (–9) + 4 + 16
(b) (37) + (–2) + (–65) + (–8)
Solutions:
(a) (-7) + (-9) + 4 + 16
= (-7) + (-9) + 4 + (+7) + (+9) = (-7) + (+7) + (-9) + (+9) + 4 = 0 + 0 + 4 [(-a) + (+a) = 0] = 4(b) (37) + (-2) + (-65) + (-8)
= (+37) + (-75) = (+37) + (-37) + (-38) = 0 + (-38) [(-a) + (+a) = 0] = -38Exercise 6.3 page no: 131
1. Find
(a) 35 – (20)
(b) 72 – (90)
(c) (-15) – (-18)
(d) (-20) – (13)
(e) 23 – (-12)
(f) (-32) – (-40)
Solutions:
(a) 35 – (20)
= 35 – 20 = 15(b) 72 – (90)
= 72 – 90 = -18(c) (-15) – (-18)
= -15 + 18 = 3(d) (-20) – (13)
= -20 – 13 = -33(e) 23 – (-12)
= 23 + 12 = 35(f) (-32) – (-40)
= -32 + 40 = 82. Fill in the blanks with >, < or = sign.
(a) (–3) + (–6) ______ (–3) – (–6)
(b) (–21) – (–10) _____ (–31) + (–11)
(c) 45 – (– 11) ______ 57 + (– 4)
(d) (–25) – (–42) _____ (– 42) – (–25)
Solutions:
(a) (-3) + (-6) = -9
(-3) – (-6) = -3 + 6 = 3 -9 < 3 Therefore, (-3) + (-6) < (-3) – (-6)(b) -21 – (-10) = -21 + 10 = -11
-31 + (-11) = -42 -11 > -42 Therefore, (-21) – (-10) > (-31) + (-11)(c) 45 – (-11) = 45 + 11 = 56
57 + (-4) = 57 – 4 = 53 56 > 53 Therefore, 45 – (-11) > 57 + (-4)(d) (-25) – (-42) = -25 + 42 = 17
-42 – (-25) = -42 + 25 = -17 17 > -17 Therefore, (-25) – (-42) > (-42) – (-25)3. Fill in the blanks.
(a) (–8) + _____ = 0
(b) 13 + _____ = 0
(c) 12 + (–12) = ____
(d) (–4) + ____ = –12
(e) ____ – 15 = – 10
Solutions:
(a) (-8) + 8 = 0
(b) 13 + (-13) = 0
(c) 12 + (-12) = 0
(d) (-4) + (-8) = -12
(e) 5 – 15 = -10
4. Find
(a) (–7) – 8 – (–25)
(b) (–13) + 32 – 8 – 1
(c) (–7) + (–8) + (–90)
(d) 50 – (–40) – (–2)
Solutions:
(a) (-7) – 8 – (-25) = -7 -8 + 25
= -15 + 25 = 10(b) (-13) + 32 – 8 – 1 = -13 + 32 – 8 – 1
= 32 – 22 = 10(c) (-7) + (-8) + (-90) = -7 – 8 – 90
= – 105(d) 50 – (-40) – (-2) = 50 + 40 + 2
= 92| Related Links |
NCERT Solutions for Class 6 Maths Chapter 6 Topic-Wise Discussion
Chapter 6 of Class 6 Maths is divided into four sections, and the following is a breakdown of each topic.Introduction
The Integers Class 6 NCERT chapter starts with an introduction that includes examples. It tells a story about Sunita, who needs 10 bananas for her picnic but has only 8. So, she borrows two from her neighbour. This example explains how Sunita needs to return 2 bananas to her neighbour. Other similar examples in this chapter introduce the concept of integers to students.The introduction then discusses various signs attached to numbers and what they mean.Integers
The next section discusses Integers in Class 6. Students already know about natural numbers, and in this chapter, they learn about negative integers.Various figures help students understand the concept of different numbers like whole numbers, natural numbers, negative numbers, and integers. They also learn how to represent integers using a single line. The ordering of integers comes next, where students learn how to arrange integers based on their value. With the help of NCERT solutions, students can easily understand these concepts and gain a better grasp of them.Addition of Integers
Understanding how to add integers in Class 6 is essential for exams and daily life. In this chapter, students learn this concept through an interesting example involving a boy named Mohan and steps in his house leading to the terrace and go down. Terrace steps are considered positive integers, and go down steps are negative integers, with ground level as zero. This way, students learn how to count integers by moving up and down the stairs. Other examples with dice, tiles, and buttons further simplify this concept. Students also learn how to add Class 6 Integers using a straight line.Subtraction of Integers Using a Number Line
After addition, students learn how to subtract Class 6 Maths Integers using a single line. Various methods for this process are explained in this section.Importance of NCERT Solution For Class 6 Maths Chapter 6 Integers
NCERT solutions for Class 6 Maths Chapter 6, which deals with integers, are crucial for several reasons. The National Council of Educational Research and Training (NCERT) develops these solutions to complement the textbook and enhance the learning experience of students. Here's a detailed explanation of why NCERT solutions for Class 6 Maths Chapter 6 (Integers) are important:1. Aligned with the Curriculum: NCERT solutions are directly aligned with the curriculum prescribed by educational boards. They cover all the topics and concepts mentioned in the Class 6 Maths textbook, ensuring that students get a comprehensive understanding of the subject.
2. Clarity of Concepts: The solutions provided by NCERT are designed to offer clarity on various mathematical concepts related to integers. Clear explanations, step-by-step solutions, and illustrative examples help students grasp the underlying principles easily.
3. Structured Format: NCERT solutions follow a structured and systematic format, making it easier for students to navigate through different topics. This organization helps students to learn in a systematic manner, starting from the basics and gradually moving towards more complex concepts.
4. Exam Preparation: Class 6 lays the foundation for subsequent classes, and understanding integers is crucial for building mathematical skills. NCERT solutions provide a solid base for students, aiding them in preparing for exams. The solutions include practice questions and exercises that align with the examination pattern, allowing students to assess their understanding and practice solving problems.
5. Logical and Analytical Thinking: Integers involve concepts of positive and negative numbers, addition, subtraction, multiplication, and division. The NCERT solutions for Class 6 Maths Chapter 6 help students develop logical and analytical thinking skills, which are essential not only for mathematics but also for problem-solving in various real-life scenarios.
6. Self-Study Resource: NCERT solutions act as a valuable self-study resource. Students can use these solutions to reinforce what they have learned in class, clarify doubts, and practice problem-solving independently. This promotes a self-directed learning approach, fostering a sense of responsibility for one's own education.
7. Consistent with Educational Standards: NCERT is a reputable institution that sets educational standards in India. By using NCERT solutions, students can be confident that they are following a curriculum that meets national educational standards, ensuring a uniform and high-quality learning experience.
NCERT Solutions for Class 6 Maths Chapter 6 FAQs
How can I download NCERT solutions for Class 6 Maths?
What are the different types of integers?
What are the benefits of using NCERT solutions?
What are Integers in Maths for Class 6?
What are the different operations that can be performed on Integers?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
