CBSE Class 6 Maths Notes Chapter 11 Algebra Free PDF Available
CBSE Class 6 Maths Notes Chapter 11 Algebra is provided here. Students can use our CBSE Class 6 Maths Notes Chapter 11 and prepare better for their examinations.
Neha Tanna20 Sept, 2024
Share
CBSE Class 6 Maths Notes Chapter 11: In CBSE Class 6 Maths, Chapter 11, "Algebra," students learn the fundamentals of algebraic expressions and equations. It teaches how to express unknown numbers with variables, which are letters like x and y. This is useful for creating equations that help solve issues. The idea of expressions with variables and constants is covered in this chapter, along with how generalising patterns and rules can be done with them.
Students gain knowledge on how to solve basic equations and simplify expressions. In addition, CBSE Class 6 Maths Notes Chapter 11 emphasises how algebra may be used in everyday situations to solve word problems and identify missing values, which lays a solid foundation for further mathematical study.CBSE Class 6 Maths Notes Chapter 11 Overview
CBSE Class 6 Maths Notes Chapter 11, is a crucial subject that exposes students to the basic ideas of algebra. In order to solve mathematical problems and generalise patterns, it helps pupils grasp how to express unknown values using variables, or letters. Students' ability to formulate and simplify algebraic formulas fosters their capacity for critical thought and problem-solving. Since algebra is utilised extensively in many disciplines, including science, economics, and engineering, this chapter will be crucial to your future academic and professional endeavours. CBSE Class 6 Maths Notes Chapter 11 also establishes the foundation for more complex algebraic ideas that will be covered in later classes. Algebra is a practical and helpful mathematical tool because it helps students apply it to real-life circumstances like calculating unknown values and answering word problems.CBSE Class 6 Maths Notes Chapter 11 PDF
Below we have provided CBSE Class 6 Maths Notes Chapter 11 Algebra for the ease of the students. Students can download this CBSE Class 6 Maths Notes Chapter 11 Algebra pdf from the below link and access it without internet.CBSE Class 6 Maths Notes Chapter 11 PDF
CBSE Class 6 Maths Notes Chapter 11 Algebra
Below is the CBSE Class 6 Maths Notes Chapter 11 Algebra - In the mathematical field of algebra, letters can be used in place of numbers to find unknowns. Another way to phrase it is the process of creating equations with real-world variables and then solving them. The Arabic term "al-jabr," which signifies the mending of fractured pieces, is where the word algebra originates. Here are some practice algebraic problems for your kids.Introduction to Algebra
Variable
A variable is an unknown quantity that is prone to change with the context of a situation. Example: In the expression 2 x + 5 , x is the variable.Constant
Constant is a quantity which has a fixed value. In the given example 2 x + 5 , 5 is the constant.Terms of an Expression
Terms are components of an equation that are initially constructed independently, then added or deleted. The equation (2x+5) is created by adding the terms 2x and 5 in the example above.Factors of a Term
Terms are components of an equation that are initially constructed independently, then added or deleted. Quantities that are not further factorisable are called factors of a phrase. Factors of the phrase 2x in the example above are x and 2.Coefficient of a Term
The numerical factor of a term is called the coefficient of the term. In the above-given example, 2 is the coefficient of the term 2x.Like Terms and Unlike Terms are fundamental concepts in algebra, helping to simplify expressions.
Like Terms : These are terms that have the same variables raised to the same powers. The coefficients (numerical values) of the terms can be different, but the variable parts must be identical.
Example: 8xy and 3xy are like terms.Unlike Terms : These are terms that have different variables or the same variables raised to different powers. Unlike terms cannot be combined through addition or subtraction.
Example: 7xy and -3x are unlike terms.Monomial, Binomial, Trinomial and Polynomial Terms
| Name | Monomial | Binomial | Trinomial | Polynomial |
| No. of terms | 1 | 2 | 3 | >3 |
| Example | 7xy | (4x−3) | (3x+5y−6) | (6x+5yx−3y+4) |
Formation of Algebraic Expressions
Combinations of variables, constants and operators constitute an algebraic expression. Example: 2 x + 3 , 3 y + 4 x y , etc.Addition and Subtraction of Algebraic Expressions
Addition and Subtraction of Algebraic Expressions involve combining like terms, while unlike terms remain separate. Here's how it works:Addition and Subtraction of Like Terms
Sum of two or more like terms is a like term. Its numerical coefficient will be equal to the sum of the numerical coefficients of all the like terms. Example: 8 y + 7 y = ? 8y +7y ___________ (8+7)y = 15y ____________ Difference between two like terms is a like term. Its numerical coefficient will be equal to the difference between the numerical coefficients of the two like terms. Example: 11 z − 8 z = ? 11z −8z __________ (1-8)z = 3z ___________Addition and Subtraction of Unlike Terms
- For adding or subtracting two or more algebraic expressions, like terms of both the expressions are grouped together and unlike terms are retained as it is.
- Addition of − 5 x 2 + 12 x y and 7 x 2 + x y + 7 x is shown below:
- Subtraction of − 5 x 2 + 12 x y and 7 x 2 + x y + 7 x is shown below:
Algebra as Patterns
Algebra as Patterns refers to the use of algebra to identify, represent, and generalize patterns found in numbers, shapes, and real-life scenarios. Algebra allows students to express patterns using variables, making it easier to predict future terms and find general rules.Number Patterns
- If a natural number is denoted by n, then its successor is (n + 1). Example: Successor of n = 10 is n + 1 = 11 .
- If a natural number is denoted by n, then 2n is an even number and (2n+1) is an odd number. Example: If n = 10 , then 2 n = 20 is an even number and 2 n + 1 = 21 is an odd number.
Patterns in Geometry
There are geometric figures that exhibit patterns that algebraic equations can depict. An algebraic expression that represents the number of diagonals that can be drawn from a single vertex of a polygon with n sides is (n – 3).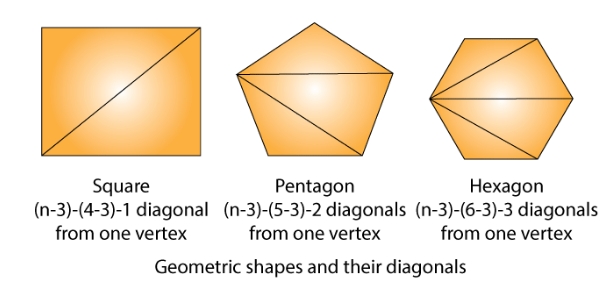
Algebraic Expressions in Perimeter and Area Formulae
-
Algebraic expressions can be used in formulating perimeter of figures.
Example: Let L be the length of one side then, the perimeter of :
- An equilateral triangle = 3L.
- A square = 4L.
- A regular pentagon = 5L.
-
Algebraic expressions can be used in formulating area of figures.
Example: Area of :
- Square = l2 where l is the side length of the square.
- Rectangle = l * b, where l and b are lengths and breadth of the rectangle.
- Triangle = 1/2 b * h where b and h are base and height of the triangle.
What Is the Equation?
A condition on a variable that can only be satisfied for a certain value of the variable is called an equation. An equality sign divides an equation's left-hand side (LHS) from its right-hand side (RHS). LHS therefore equals RHS. It is not an equation if LHS and RHS are not equal.Solving an Equation
A variable's value that makes an equation work is referred to as its solution. Using the trial and error method is one of the easiest ways to solve an equation.Benefits of CBSE Class 6 Maths Notes Chapter 11
CBSE Class 6 Maths Notes Chapter 11 FAQs
What are the 5 basic rules of algebra?
The basic rules of algebra are the commutative rule of addition, the commutative rule of multiplication, the associative rule of addition, the associative rule of multiplication, and the distributive property of multiplication.
What is algebra used for?
Algebra is the study of mathematical symbols and the rules for manipulating those symbols.
What is the basis of algebra?
The basics of algebra include numbers, variables, constants, expressions, equations, linear equations, and quadratic equations.
What is first principles of algebra?
Derivative by the first principle refers to using algebra to find a general expression for the slope of a curve. It is also known as the delta method. The derivative is a measure of the instantaneous rate of change. y = f(x) with respect to its variable x.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.