CBSE Class 6 Maths Notes Chapter 12 Ratio and Proportion
CBSE Class 6 Maths Notes Chapter 12 Ratio and Proportion is provided here. Students can use our CBSE Class 6 Maths Notes Chapter 12 and prepare better for their examinations.
Neha Tanna23 Sept, 2024
Share
CBSE Class 6 Maths Notes Chapter 12: The fundamentals of utilising a ratio to compare two amounts are introduced to students in Chapter 12 of CBSE Class 6 Maths, Ratio and Proportion. The number of times one quantity is larger or smaller than another is displayed by a ratio. It is stated as a fraction or with the colon (:) symbol, for example, 3:5. Conversely, the proportional equation asserts the equality of two ratios.
By breaking down ratios and figuring out if two given ratios add to a proportion, students can answer issues involving ratios and proportions. The chapter also covers real-world applications for enhanced comprehension.CBSE Class 6 Maths Notes Chapter 12 Overview
The CBSE Class 6 Maths syllabus's Chapter 12, Ratio and Proportion, is crucial because it lays the foundation for comprehending relationships between amounts. The idea of ratio is introduced in this chapter, which is useful for comparing two amounts or numbers. It also discusses proportion, a crucial concept that aids in determining whether two ratios are equal. Understanding these ideas is essential for resolving issues in daily life, such calculating costs, understanding maps, and scaling recipes. Higher education classes, where ratio and proportion are employed in complex subjects like percentages, speed, time, probability, and geometry, will find this chapter to be very important. This chapter serves as a foundational topic in mathematics by assisting in the development of analytical and problem-solving skills that are useful not just for exams but also for real-world applications in a variety of sectors, including science, engineering, and finance.CBSE Class 6 Maths Notes Chapter 12 PDF
Below we have provided CBSE Class 6 Maths Notes Chapter 12 Ratio and Proportion for the ease of the students. Students can download this CBSE Class 6 Maths Notes Chapter 12 Ratio and Proportion pdf from the below link and access it without internet.CBSE Class 6 Maths Notes Chapter 12 PDF
CBSE Class 6 Maths Notes Chapter 12 Ratio and Proportion
Below is CBSE Class 6 Maths Notes Chapter 12 Ratio and Proportion - Ratios are mathematical quantities that are used to compare two objects that are similar to one another in terms of units. There are three methods to write a ratio: x to y, x: y, and
Ratio is the concept of comparing items that are similar to one another. Additionally, two ratios are said to be in proportion to one another when they are equal. '::' or '=' is the symbol used to symbolise it.
Introduction to Ratio and Proportion
A ratio is a comparison between two quantities that shows how many times one quantity is contained in another. It is expressed as: A:B A proportion is an equation that shows two ratios are equivalent. If two ratios A/B and C/D are equal, then they form a proportion, represented as: A:B :: C:DKey Differences between Ratio and Proportion:
- Ratio compares two quantities directly.
- Proportion states that two ratios are equal.
Golden Ratio
If the ratio of two quantities equals the ratio of their sum to the bigger of the two quantities, then the two quantities are in the golden ratio.
Ratio
A comparison of one quantity with regard to another is called a ratio. The symbol for it is ":“. Only when two quantities are in the same unit can they be compared.Example: Father’s age is 75 years and the daughter’s age is 25 years.
⇒ The ratio of father’s age to daughter’s age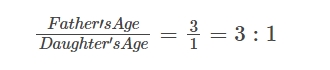
Difference between Fractions and Ratios
A fraction's denominator denotes the total number of pieces, and it describes a portion of a whole. 13 is an example of one part out of three. A ratio is the result of comparing two distinct amounts. As an illustration, consider a society where 10 members enjoy driving, 20 enjoy swimming, and 30 members in total. The percentage of people who enjoy driving compared to the entire population is 10:30. The percentage of respondents who prefer swimming versus those who prefer driving is 20:10.Same Ratio in Different Situations
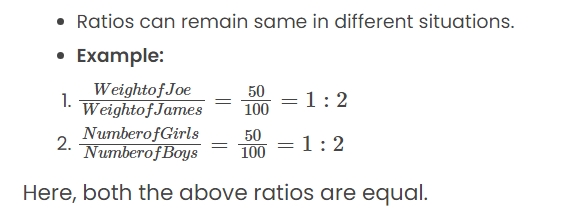
Comparing Quantities Using Ratios
Equivalent Ratios
The ratios are referred to as equivalent ratios when they are equal. By multiplying and dividing the numerator and denominator by the same number, equivalent ratios can be calculated. For instance, the ratios 10:30 (=1:3) and 11:33 (=1:3) are comparable.Unitary Method
The Unitary Method is a technique where the value of one unit is found first, followed by the value of the necessary number of units.
Applications of the Unitary Method:
- Shopping: Determining the cost of several items when the cost of one is known.
- Time and work: Calculating the time required to complete tasks based on the rate of work.
- Distance, speed, and time: Finding distances or times using speed as a factor.
- Conversions: Used to convert units (e.g., kilometers to miles, currency conversion).
Proportions
If two ratios are equal, then they are said to be in proportion.
Uses of Ratios and Proportions
-
Example:
Suppose a man travelled 80 km in 2 hours, how much time will he take to travel 40 km?
Solution: If x is the required time, then the proportion is
80 : 2 : : 40 : x .
Benefits of CBSE Class 6 Maths Notes Chapter 12
The Ratio and Proportion chapter in CBSE Class 6 Maths offers several benefits:Foundation for Advanced Concepts : It builds the groundwork for understanding more complex topics like percentages, algebra, speed, and probability in higher grades.
Real-Life Application : Students can apply ratio and proportion concepts in everyday situations, such as comparing prices, resizing recipes, or understanding maps and scales.
Enhanced Problem-Solving Skills : The chapter fosters logical thinking and analytical skills, enabling students to approach mathematical problems systematically.
Preparation for Competitive Exams : Many competitive exams include questions on ratio and proportion, making mastery of these topics essential for future academic success.
Conceptual Clarity : The chapter reinforces basic arithmetic and number sense, helping students gain confidence in handling numbers.
CBSE Class 6 Maths Notes Chapter 12 FAQs
How are ratio and proportion used in real life?
Ratios, which are mathematical relationships, are excellent real-world examples of math. Cooking, grocery shopping, and getting from one place to another place are 3 main real-life scenarios where ratios are not only common but also necessary for proper, cost-effective performance.
What are the rules of ratio and proportion?
Ratio is used for comparing two quantities of the same kind. The ratio formula for two numbers, a and b is expressed as a : b or a/b. When two or more ratios are equal, they are said to be in proportion.
How important is ratio and proportion?
Ratios and proportions are foundational to student understanding across multiple topics in mathematics and science. In mathematics, they are central to developing concepts and skills related to slope, constant rate of change, and similar figures, which are all fundamental to algebraic concepts and skills.
Who discovered ratio and proportion?
The Pythagoreans
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.