CBSE Class 6 Maths Notes Chapter 13 Symmetry PDF Download
CBSE Class 6 Maths Notes Chapter 13 Symmetry is provided here. Students can use our CBSE Class 6 Maths Notes Chapter 13 and prepare better for their examinations.
Neha Tanna23 Sept, 2024
Share
CBSE Class 6 Maths Notes Chapter 13: Geometry requires an understanding of symmetry. Students study line symmetry, in which one half of a figure is the mirror image of the other half, in Class 6 CBSE Maths, Chapter 13 on Symmetry. If two figures can be folded along a line and match exactly, the figure is said to be symmetrical. We refer to this line as the line of symmetry.
Geometric shapes like squares, equilateral triangles, and circles are typical examples. Additionally, the chapter explains reflection symmetry and challenges students to point out symmetrical items in their daily environment.CBSE Class 6 Maths Notes Chapter 13 Overview
CBSE Class 6 Maths Notes Chapter 13 Symmetry, is a crucial introduction to the idea of symmetry, which is important in both mathematics and everyday life. The basic concept of line symmetry—that is, the ability to split a figure into two identical halves along a line of symmetry—is explained to students in this chapter. Students' spatial awareness and visualisation abilities, which are essential in geometry and other mathematical subjects, are improved by learning about symmetry. Another important idea in nature, design, architecture, and the arts is symmetry. Critical thinking and analytical abilities are developed through the recognition of symmetrical patterns in objects and shapes. Students who study this chapter will be able to connect mathematical ideas to real-world situations, which will prepare them for more advanced geometry themes in later classes.CBSE Class 6 Maths Notes Chapter 13 PDF
Below we have provided CBSE Class 6 Maths Notes Chapter 13 Symmetry for the ease of the students. Students can download this CBSE Class 6 Maths Notes Chapter 13 Symmetry pdf from the below link and access it without internet.CBSE Class 6 Maths Notes Chapter 13 PDF
CBSE Class 6 Maths Notes Chapter 13 Symmetry
Below is the CBSE Class 6 Maths Notes Chapter 13 Symmetry - When one side of an object is a mirror image of the other, it is said to have symmetry. When something is divided in half, the two halves are identical. The line of symmetry is the one that separates them. A basic illustration of this is reflection symmetry. There are one or more lines of symmetry that divide the object. Below are some types of line of symmetry along with examples-| S.NO | Type | Example |
| 1 | No line of symmetry | Scalene triangle |
| 2 | 1 line of symmetry | Isosceles triangle |
| 3 | 2 lines of symmetry | Rectangle |
| 4 | 3 lines of symmetry | Equilateral triangle |
Introduction to Symmetry
A basic idea in both mathematics and nature, symmetry refers to harmony and balance in forms and objects. If an object or figure can be divided into two or more identical components and organised in a balanced manner, then it is said to be symmetrical. There are several types of symmetry, including rotational symmetry (which allows a figure to be rotated less than 360 degrees and still look the same), point symmetry (which allows a figure to look the same when rotated 180 degrees), and line symmetry (which allows a figure to be divided into two matching halves along a line). Comprehending symmetry is essential to geometry and design because it facilitates the identification of patterns and structures in both the natural and artificial worlds. When figures have equally balanced proportions, they are said to be symmetrical.Bilateral Symmetry
Bilateral symmetry occurs when a figure has only one line dividing it into its two parts, and these halves fully overlap one another. An illustration of bilateral symmetry is a butterfly.
Line Symmetry
If a line can be drawn that divides a figure into two symmetrical sections, then the figure has line symmetry. It is known as a line of symmetry. Example: Line symmetry is shown in the following figures by the dotted lines.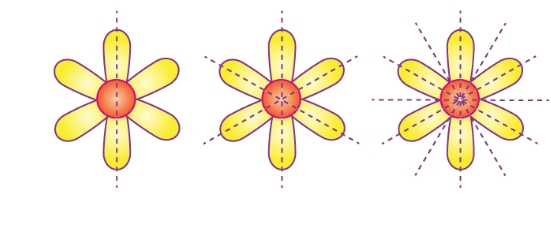
Lines of Symmetry
There can be an infinite number of lines of symmetry that cross a figure. Some may have one, two, or even more symmetrical lines. A single line of symmetry example: a lock on the door.
Point Symmetry and Reflection Symmetry
Point Symmetry and Reflection Symmetry are two types of symmetry commonly studied in geometry. Here's a brief explanation of each:
Reflection Symmetry
Reflection symmetry is very similar to line symmetry except for the change in orientation.
For example, when you view yourself in the mirror, your right hand becomes the left hand in the mirror.
Point Symmetry
When a figure is drawn around a single centre point, point symmetry occurs. It applies to figures that have a point where the symmetry can be determined. The centre of symmetry is this point. The hourglass, for instance, exhibits point symmetry.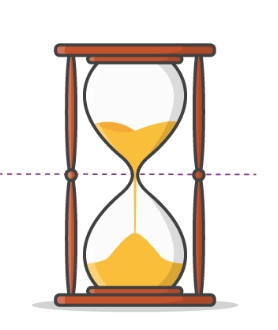
Kaleidoscope
A kaleidoscope uses mirrors to produce images that have several lines of symmetry.
Usually, a V-shaped configuration of two mirror strips is utilised.
The number of lines of symmetry is determined by the angle between the mirrors.
The kaleidoscope pattern is depicted in the figure below.
Benefits of CBSE Class 6 Maths Notes Chapter 13
The benefits of studying CBSE Class 6 Maths Chapter 13 on Symmetry include:Improved Spatial Understanding : Symmetry helps students develop better spatial awareness by visualizing how shapes and objects can be divided into identical halves.
Foundation for Advanced Geometry : It lays the groundwork for more complex geometrical concepts like transformations, reflections, and rotations studied in higher classes.
Application in Real Life : Symmetry is present in nature, architecture, and design, making the concept practical and relatable for students.
Enhanced Analytical Skills : Identifying lines of symmetry and symmetrical patterns enhances logical thinking and problem-solving skills.
Aesthetic Appreciation : Understanding symmetry helps students appreciate art, design, and patterns, as many aesthetic structures rely on symmetrical balance.
Boosts Critical Thinking : The chapter encourages critical thinking as students observe and explore symmetry in everyday objects and environments.
CBSE Class 6 Maths Notes Chapter 13 FAQs
What are the rules of symmetry?
If an object is symmetrical, it means that it is equal on both sides. Suppose if we fold a paper such that half of the paper coincides with the other half of the paper, then the paper has symmetry. Symmetry can be defined for both regular and irregular shapes.
How is symmetry used in everyday life?
Symmetry also offers human beings an additional extension to their capabilities. For example, two eyes are necessary for stereoscopic vision. Two ears help us get a better 3-dimensional sensation of hearing. (i)Radial symmetry: The organism looks like a pie.
What is the concept of symmetry?
Mathematically, symmetry means that one shape becomes exactly like another when you move it in some way: turn, flip or slide. For two objects to be symmetrical, they must be the same size and shape, with one object having a different orientation from the first.
Which one has highest symmetry?
The most symmetrical one is the cubic system and the least symmetrical is the triclinic one. Between those to extreme cases ,you can find five additional one.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
