

CBSE Class 6 Maths Notes Chapter 4: CBSE Class 6 Maths Notes Chapter 4 Basic Geometrical Ideas introduces fundamental concepts of geometry. It covers essential terms like points, lines, line segments, rays, and angles. Students learn how to identify and differentiate between these concepts.
The chapter explains types of lines such as parallel and intersecting lines, and introduces curves, polygons, and circles. It also discusses the components of a circle, like the radius, diameter, chord, and arc. Through clear explanations and diagrams, students develop a basic understanding of geometry that forms the foundation for advanced concepts in higher classes.CBSE Class 6 Maths Notes Chapter 4 Overview
CBSE Class 6 Maths Notes Chapter 4 Basic Geometrical Ideas is important because it introduces the foundational elements of geometry, which are essential for understanding shapes and structures in the world around us. The chapter begins with the concept of a point, the simplest figure in geometry, and builds up to lines, line segments, rays, and angles. It also explores different types of lines, like parallel and intersecting lines, along with curves and polygons. Circles are a key focus, and students learn important terms like radius, diameter, and chord. This chapter lays the groundwork for more complex geometrical concepts in higher grades, helping students visualize and understand shapes. By mastering these basic ideas, students can better grasp the logic behind figures and measurements, making this chapter crucial for anyone starting their journey in mathematics and geometry.CBSE Class 6 Maths Notes Chapter 4 PDF
Below we have provided CBSE Class 6 Maths Notes Chapter 4 Basic Geometrical Ideas pdf for the ease of the students so that they can download it and access it without internet.CBSE Class 6 Maths Notes Chapter 4 PDF
CBSE Class 6 Maths Notes Chapter 4 Basic Geometrical Ideas
Below is the CBSE Class 6 Maths Notes Chapter 4 Basic Geometrical Ideas - Several geometric terms that are crucial in higher classes are given in this chapter. In addition to helping students establish a foundation in geometry, the topics covered will make it easier for them to understand concepts that will be covered in higher grades. The main topics covered here are-- Basic Definitions in Geometry
- Polygons
- Triangles
- Quadrilaterals
- About Circles
Basic Definitions in Geometry
| Terms | Definition |
| Point | It determines a location and is usually determined by a capital letter. |
| Line segment | The shortest distance between two points is called a line segment. |
| Line | By extending a line segment indefinitely on both sides, a line is obtained. |
| Intersecting lines | If two distinct lines meet or cross at a point, they are called intersecting lines. |
| Parallel lines | Parallel lines are lines which are always the same distance apart and never intersect anywhere in a plane. |
| Ray | A ray is a line which starts from a particular point and goes infinitely towards a particular direction. |
| Curve | It is a drawing which is done without lifting the pencil. |
| Simple curve | A curve that never crosses itself is a simple curve. |
| Closed and open curves | A curve is closed if its ends are joined. Otherwise, it is an open curve. |
| Angle | It is made up of two rays which are starting from a common point. |
Polygons
A closed curve composed of line segments is referred to as a polygon. There are many different kinds of polygons, including triangles, quadrilaterals, pentagons, and more. Triangles have three line segments, quadrilaterals have four, and so on. A few key phrases associated with polygons are:| Terms | Definition |
| Sides of a polygon | The line segments are known as the sides of the polygon. |
| Adjacent sides | Two points having the same endpoint are called adjacent sides. |
| Vertex | Vertex is the meeting or intersecting point of a pair of sides. |
| Diagonal | Diagonal is obtained by joining any two non-adjacent vertices of a polygon. |
T riangles
A triangle is as a polygon having three line segments or sides. A triangle ABC is written asas given below-
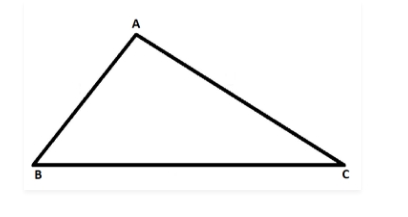
In this triangle, AB, BC, and AC are sides of the triangle and A, B, C are the vertices of the triangle. Also, the angle between BC and AB is the
Quadrilaterals
A quadrilateral is a four-sided polygon, meaning that it has four sides, or line segments, and four angles as a result. For easier comprehension, a quadrilateral's diagram is provided. A quadrilateral's vertices are called in a cyclic fashion, it should be noted.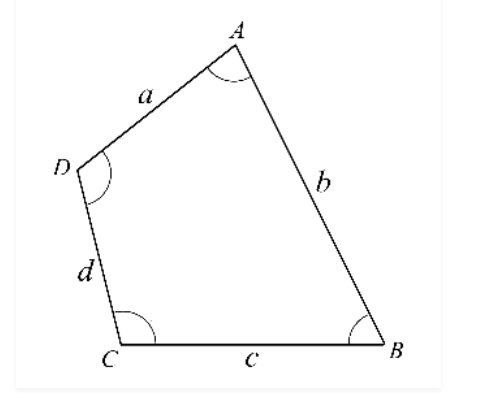 AD and DC are two instances of neighbouring sides in this diagram. Moreover, AD and BC are two opposing viewpoints. Angles A and C are in opposition to one another here. The line segment in this becomes a diagonal if it is drawn from A to C or from B to D.
AD and DC are two instances of neighbouring sides in this diagram. Moreover, AD and BC are two opposing viewpoints. Angles A and C are in opposition to one another here. The line segment in this becomes a diagonal if it is drawn from A to C or from B to D.
About Circles
A closed figure produced by a collection of points in a plane that are spaced equally apart from a fixed point that serves as the circle's centre is known as a circle. Several key phrases associated with circles are:| Terms | Definitions |
| Radius | The fixed distance at which the points are located from the centre is called the radius. |
| Diameter | Diameter is the length of a line segment which joins any two points on the circle by passing through the centre. Diameter is always double than the radius. |
| Circumference | The distance around the circle is known as its circumference or perimeter. |
| Chord | A line segment joining any two points on the circle is a chord. |
| Sector | It is the region in the interior of a circle which is enclosed by an arc on one side and a pair of radii on the other two sides. |
| Segment | It is a region in the interior of the circle enclosed by an arc and a chord. |
Points
- A point determines a specific location.
- They are denoted by any capital letter of the English Alphabet.
Curves
- In simple terms, any line that is not straight is said to be a curve.
- If a curve does not cross itself, then it is called a simple curve.
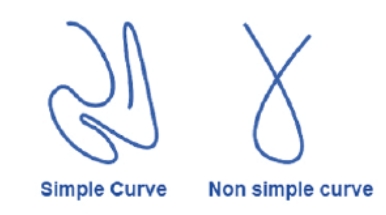
Closed and Open Curves
If the ends of a curve are connected, it is considered closed. An open curve is defined as one whose endpoints are open.Polygons
A simple closed figure made up of line segments is called a polygon.Terms Related to Polygons
Some of the important terms related to a polygon are :

- Vertex: The meeting point of a pair of sides. Here A, B, C, D and E are the vertices of the polygon.
- Adjacent sides: Any two sides of a polygon with a common endpoint. Here AB and BC are adjacent sides.
- Adjacent vertices: Endpoints of the same side of a polygon. Here A and B are the adjacent vertices.
- Diagonals: The lines joining the non-adjacent vertices of a polygon. Here AC, AD, BD, BE and CE are the diagonals.
Triangle
A polygon with three sides is a triangle. It is composed of three vertices, three angles, and three sides. It consists of an outside and an inside zone. In the above figure:
In the above figure:

Quadrilaterals
A polygon with four sides, four angles, and four vertices is called a quadrilateral. In a quadrilateral ABCD:
In a quadrilateral ABCD:
- AB, BC, CD and DA are the sides of the quadrilateral.
- A, B, C and D are the vertices.
- AB and CD, and BC and DA are the pairs of opposite sides.
- Angle A and angle C, and angles B and D are the pairs of opposite angles.
- Angle A is adjacent to angle B and angle D. Similar relations exist for all other angles.
Angles
Two rays that begin at the same endpoint form an angle. We refer to these rays as the angle's arms. The vertex of the angle is the name given to the shared terminal. The angle's vertex must be in the centre when designating the angle. Ray OP and Ray OQ, for instance, make an angle. It has the symbol ∠POQ.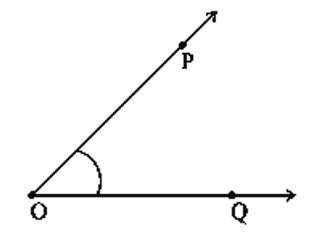 Ray OP and OQ are the arms or sides of the angle. O is the vertex of the angle POQ
Ray OP and OQ are the arms or sides of the angle. O is the vertex of the angle POQ
Exterior and Interior Points to an Angle
Its plane is divided into three sections by an angle. The angles, their interiors, and their exteriors are these places. In the figure above, points F and R lie in the interior of ∠ABC. Points A, B and C lie on the angle ∠ABC and P, X, and T lie on the exterior of angle ∠ABC.
In the figure above, points F and R lie in the interior of ∠ABC. Points A, B and C lie on the angle ∠ABC and P, X, and T lie on the exterior of angle ∠ABC.
Circles
A circle isn't a polygon; it's just a straightforward closed curve. In essence, a circle is created when a point moves away from a fixed point at a defined distance.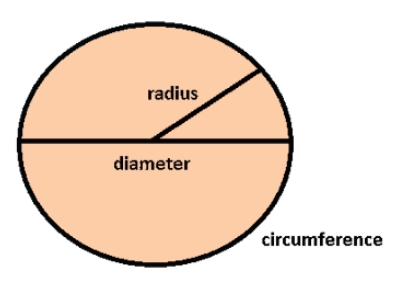 The centre is this fixed location in the middle.
The circumference is the distance a point travels around a circle.
The centre is this fixed location in the middle.
The circumference is the distance a point travels around a circle.
Terms Related to Circle
A line segment connecting any two points on a circle is called its chord. A diameter is a chord that goes through a circle's centre. A circle's diameter splits it into two equal parts, known as semicircles. A sector is an area inside a circle that is bounded by two radii on two of its sides and an arc on one of its sides.
A segment is an area inside a circle that is bounded by an arc and a chord.
A sector is an area inside a circle that is bounded by two radii on two of its sides and an arc on one of its sides.
A segment is an area inside a circle that is bounded by an arc and a chord.
All About Lines
Line Segment


Lines
A line segment is defined as one that can be infinitely extended on both sides. This is a line, m. It has an endless amount of points on it.
Ray
A segment of a line is called a ray. It begins at what is known as its starting point and continues indefinitely in the opposite direction.
Intersecting and Parallel Lines
Two lines are said to intersect when they share a point. Since lines l and m in this instance share a point P, they intersect at P, which serves as the intersection point.
Two lines are considered parallel if they do not share a point. Here, the lines AB and CD are parallel.
Since lines l and m in this instance share a point P, they intersect at P, which serves as the intersection point.
Two lines are considered parallel if they do not share a point. Here, the lines AB and CD are parallel.

Position in a Figure
The components of a closed curve are threefold. In the following figure, N is outside the curve, M is on the border, and L is inside the curve. The region of a curve is the inside of the curve plus its boundary.
The region of a curve is the inside of the curve plus its boundary.
Benefits of CBSE Class 6 Maths Notes Chapter 4
The benefits of studying CBSE Class 6 Maths Notes for Chapter 4, "Basic Geometrical Ideas," include:Foundation for Geometry : It introduces the fundamental concepts of geometry, such as points, lines, angles, and shapes, which are essential for understanding advanced mathematical concepts in future classes.
Improves Visualization : The chapter helps students visualize shapes, angles, and spatial relationships, improving their ability to interpret and analyze the world around them.
Boosts Problem-Solving Skills : Understanding basic geometrical ideas enhances students' logical reasoning and problem-solving skills, especially when dealing with measurements and figures.
Practical Applications : The concepts learned in this chapter have practical applications in fields like architecture, engineering, art, and design.
Enhances Mathematical Vocabulary : The chapter builds students’ vocabulary related to geometry, aiding better communication of mathematical ideas.
CBSE Class 6 Maths Notes Chapter 4 FAQs
What is the use of basic geometrical ideas?
What is a geometric idea?
What is the purpose of geometric?
Who is called the father of geometry?
Is CBSE Class 6 Maths Notes Chapter 4 Basic Geometrical Ideas useful?











