
The centroid of triangle Formula is the point where its medians intersect. Before delving into this point of intersection, let's examine the concept of medians in a triangle. Medians are line segments drawn from each vertex to the midpoint of the opposite side. Remarkably, each median divides the triangle into two smaller triangles of equal area. The point where these medians intersect is known as the centroid. Unlike other points of intersection in a triangle, the centroid always resides within the triangle.
Within this article, we will comprehensively explore the centroid of a triangle, often referred to as the centroid, covering its formula and properties. Our journey will involve gaining a deeper understanding of this concept through solved examples and practice questions.What is the Centroid of a Triangle?
The centroid of triangle arises from the intersection of its three medians, making it one of the four key points where certain elements of a triangle converge. Medians are established by connecting the vertices of a triangle to the midpoint of the side opposite each vertex. To visualize, refer to the accompanying diagram illustrating the triangle's centroid.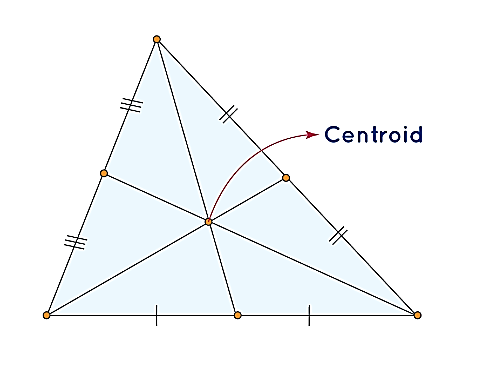
Centroid of Triangle Properties
The subsequent statements outline the distinguishing properties of a triangle's centroid, setting it apart from other points of concurrency:- The centroid serves as the geometric center of the entity.
- It materializes as the precise intersection point for all three medians of the triangle.
- The centroid divides each median in a consistent 2:1 ratio.
- This pivotal point always resides within the confines of the triangle itself.
Also Check - LCM and HCF Formula
Centroid of Triangle Formula
The formula for determining the centroid of a triangle employs the coordinates of its vertices. This calculation hinges on the availability of vertex coordinates. The centroid's coordinates are found using the following equation: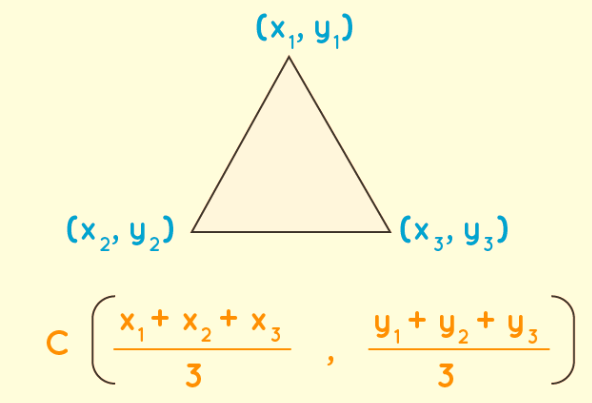 C(x,y) = (x1 + x2 + x3)/3, (y1 + y2 + y3)/3
In this equation, x1, x2, and x3 represent the 'x-coordinates' of the triangle's vertices, while y1, y2, and y3 denote the 'y-coordinates' of those vertices.
To better grasp this concept, refer to the accompanying illustration which illustrates the vertex coordinates of the triangle.
C(x,y) = (x1 + x2 + x3)/3, (y1 + y2 + y3)/3
In this equation, x1, x2, and x3 represent the 'x-coordinates' of the triangle's vertices, while y1, y2, and y3 denote the 'y-coordinates' of those vertices.
To better grasp this concept, refer to the accompanying illustration which illustrates the vertex coordinates of the triangle.
Also Check - Area of a Hexagon Formula
Difference Between Orthocenter and Centroid of Triangle
Distinguishing between the orthocenter and the centroid of a triangle encompasses several types of disparities. The primary distinctions between these two points within a triangle are elucidated in the following table:| Orthocenter | Centroid |
|---|---|
| The orthocenter is the intersection point of the altitudes. | The centroid is the intersection point of the medians. |
| It may lie outside of the triangle | It always lies inside the triangle. |
| There is not a particular ratio into which it divides the altitudes. | The medians are divided into a 2:1 ratio by the centroid. |
Difference Between Incentre and Centroid of Triangle
The centroid and the incenter exhibit diverse discrepancies contingent on the specific type of triangle they are positioned in. The significant contrasts between the orthocenter and the centroid of a triangle are outlined in the provided table:| Incenter | Centroid |
|---|---|
| The incenter is the intersection point of the angle bisectors. | The centroid is the intersection point of the medians. |
| It always lies inside the triangle. | It always lies inside the triangle. |
| There is not a particular ratio into which it divides the angle bisectors. | The medians are divided into a 2:1 ratio by the centroid. |
Important Notes on Centroid of Triangle
- The point where the medians of a triangle intersect is known as the centroid.
- It invariably resides within the triangle's boundaries.
- The centroid divides each median in a consistent ratio of 2:1.
Also Check - Area of a Rectangle Formula
Centroid of a Triangle Examples
Example 1: Given the vertices of a triangle as (4,3), (6,5), and (5,4), determine the position of the triangle's centroid. Solution: In order to locate the centroid of the triangle, we have the vertex coordinates: (x1, y1) = (4, 3) (x2, y2) = (6, 5) (x3, y3) = (5, 4) Applying the centroid formula: Centroid of a triangle = C(x,y) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3) = ((4 + 6 + 5)/3, (3 + 5 + 4)/3) = (15/3 , 12/3) = (5 , 4) Answer: The centroid of the triangle is located at the coordinates (5 , 4). Example 2: Calculate the centroid of a right-angled triangle by employing the centroid formula, with vertex coordinates given as (0,5), (5,0), and (0,0). Solution: For determining the centroid of the triangle, the provided vertices are: (x1, y1) = (0,5) (x2, y2) = (5,0) (x3, y3) = (0,0) Utilizing the centroid formula: C(x,y) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3) = ((0 + 5 + 0)/3, (5 + 0 + 0)/3) = (5/3 , 5/3) Answer: The centroid of the right-angled triangle is positioned at the coordinates (5/3, 5/3). Example 3: The vertices of a triangle are (1, 2), (h, −3), and (−4, k) and the coordinates of the centroid of the triangle are (5, –1). Find the value of h and k. Solution: We have (x1, y1) = (1, 2) (x2, y2) = (h, –3) (x3, y3) = (–4, k) Using centroid of triangle formula, we have C(x,y) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3) ⇒ (5, -1) = ((1 + h – 4)/3, (2 - 3 + k)/3) ⇒ (5, -1) = ( (-3 + h)/3, (-1 + k)/3 ) ⇒ (h - 3)/3 = 5 and (k - 1)/3 = -1 ⇒ h - 3 = 15 and k - 1 = -3 ⇒ h = 18 and k = -2 Answer: The values of h and k are h = 18 and k = -2.Centroid of Triangle Formula FAQs
Define the term Centroid.
The centroid of a triangle is created at the intersection point of its three medians. This specific point is among the four key points where certain elements within a triangle intersect.
What is the formula for the Centroid of a Triangle?
The centroid of a triangle can be calculated using the formula: C(x,y) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3), where x1, x2, and x3 represent the 'x-coordinates' of the triangle's vertices, and y1, y2, and y3 correspond to the 'y-coordinates' of the triangle's vertices.
Explain the properties of the Centroid of a Triangle.
The subsequent statements outline the distinguishing properties of a triangle's centroid, setting it apart from other points of concurrency:
The centroid serves as the geometric center of the entity.
It materializes as the precise intersection point for all three medians of the triangle.
The centroid divides each median in a consistent 2:1 ratio.
This pivotal point always resides within the confines of the triangle itself.
Explain the easiest method of calculating the centroid of a Triangle.
The process of determining the centroid of a triangle can be distilled into three fundamental steps:
Identify and record the coordinates of all three vertices.
Sum the x-coordinates of the vertices and then divide the total by 3.
Sum the y-coordinates of the vertices and then divide the total by 3.
The resulting values from step 2 and step 3 will collectively define the centroid of the triangle.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App









