
As per the LCM and HCF Formula for Calculating the highest common factor (HCF) and least common multiple (LCM) of a given set of numbers involves various techniques, such as the division method and the prime factorization method. HCF, also known as the greatest common divisor (GCD), is the largest number that divides multiple given numbers without leaving any remainder. On the other hand, the LCM of two or more numbers is the smallest multiple that is evenly divisible by all those numbers.
A solid grasp of HCF and LCM in mathematics is essential, as it equips us to address everyday situations involving grouping and sharing. Exploring the diverse methods employed to determine the HCF and LCM of numbers offers valuable insights into these concepts.
What is LCM and HCF Formula?
HCF, also known as the highest common factor or greatest common divisor (GCD), is the largest shared factor among two or more given numbers. For instance, in the numbers 24 and 36, the HCF is 12 because it's the greatest number that can evenly divide both.
Likewise, the Least Common Multiple (LCM) is the smallest number that is a multiple of the given numbers. Take the numbers 8 and 16 as an example. The multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, and so on. The multiples of 16 are 16, 32, 48, 64, 80, 96, and so on. The smallest value common to both lists is the LCM for 8 and 16, which is 16.
Understanding how to find the HCF and LCM of numbers is crucial for solving problems related to common factors and multiples.
Also Check - Area of a Hexagon Formula
How to Find HCF and LCM?
Several methods are employed to determine the Highest Common Factor (HCF) and Least Common Multiple (LCM) of numbers. Among the most frequently used methods are:
- Prime Factorization Method
- Division Method
These methods are widely employed for calculating the HCF and LCM of numbers. Let's delve into each of these methods in depth.
Download PDF LCM and HCF Formula
Finding HCF and LCM by Prime Factorization
Through the prime factorization method, both the Highest Common Factor (HCF) and the Least Common Multiple (LCM) of given numbers can be calculated. The process is explained below:
HCF by Prime Factorization:
Identify the prime factors of the given numbers.
Find the common prime factors of these numbers.
Multiply the common prime factors together, taking the ones with the lowest power if applicable.
For instance, let's calculate the HCF of 50 and 75:
Prime factors of 50: 2 × 5 × 5 (or 2 × 5²)
Prime factors of 75: 3 × 5 × 5 (or 3 × 5²)
Common factors: 5²
HCF of (50, 75) = 25
LCM by Prime Factorization:
List the prime factors of the given numbers.
Express these prime factors in exponent form.
Determine the product of prime factors with the highest powers.
Also Check - Circles formula
Example 1: Calculating the LCM of 160 and 90:
Prime factors of 160: 2 × 2 × 2 × 2 × 2 × 5 (or 2⁵ × 5)
Prime factors of 90: 2 × 3 × 3 × 5 (or 2 × 3² × 5)
Highest powers: 2⁵, 3², 5
LCM of (160, 90) = 1440
Example 2: Finding the LCM of 30 and 60:
Prime factors of 30: 2 × 3 × 5 (or 2 × 3 × 5)
Prime factors of 60: 2 × 2 × 3 × 5 (or 2² × 3 × 5)
Highest powers: 2², 3, 5
LCM of (30, 60) = 60
Using the prime factorization method, you can efficiently compute the HCF and LCM of numbers.
Finding HCF and LCM by Division Method
There exist two distinct approaches to applying the division method in order to compute LCM and HCF. Let's explore each method individually.
HCF by Division Method:
- To determine the HCF using the division method, proceed as follows:
- Initiate by dividing the larger number by the smaller number and record the remainder.
- Employ the obtained remainder as the new divisor and the preceding divisor as the new dividend, and execute the division again.
- Reiterate this division process until the remainder becomes 0.
- The last divisor in this sequence will be the HCF of the given numbers.
For instance, grasp this method through the following example:
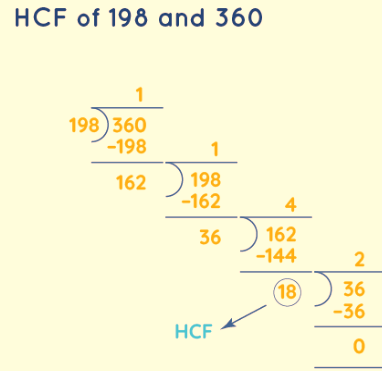
Example: Calculate the HCF of 198 and 360 using the division method.
Solution: Understand the process by referring to the steps and the accompanying illustration below:
Step 1: Divide 360 by 198. The resulting remainder is 162.
Step 2: Make 162 the divisor and 198 the dividend, then perform the division anew. This yields a remainder of 36.
Step 3: Employ 36 as the divisor and 162 as the dividend, and perform the division again. The outcome is a remainder of 18.
Step 4: Employ 18 as the divisor and 36 as the dividend, and conduct the division again. The remainder now becomes 0.
Step 5: The final divisor in this sequence, 18, signifies the HCF of 360 and 198.
Also Check - Polynomials formula
This is how the division method is employed to ascertain the HCF of two numbers.
LCM by Division Method
To ascertain the Least Common Multiple (LCM) of numbers through the division method, we repeatedly divide the numbers by prime numbers until we obtain only 1 in the final row. Follow the provided steps to comprehend the process of finding the LCM using the division method. Let's illustrate this approach using an example.
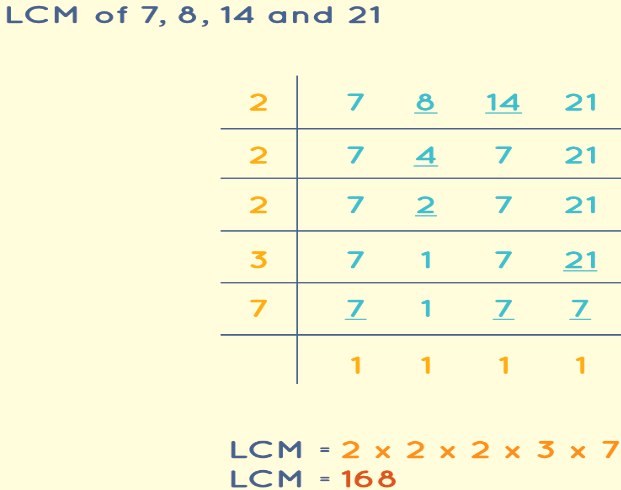
Example: Calculate the Least Common Multiple (LCM) of 7, 8, 14, and 21 using the division method.
Solution:
Follow the steps below and refer to the provided illustration:
Step 1: Begin by dividing the numbers by the smallest prime number that can divide at least one of the given numbers. In this case, divide 7, 8, 14, and 21 by the smallest prime number, 2.
Step 2: Note the quotients of the divisible numbers beneath the original numbers in the subsequent row. Maintain the other numbers as they are. Consequently, the next row reads: 7, 4, 7, and 21.
Step 3: Progress to the next division step, using the obtained quotients as the new dividends. Perform the division again and note the quotient beneath each number. In this step, only 4 was divisible by 2, so the other three numbers remain unchanged: 7, 2, 7, and 21.
Step 4: Continue this process of division, repeating steps and dividing the new dividends until you reach 1.
Step 5: Multiply all the prime numbers on the left side of the bar to obtain the LCM of the given numbers. In this case, it will be 2 × 2 × 2 × 3 × 7 = 168. Therefore, the LCM of 7, 8, 14, and 21 is 168.
This demonstrates how the division method can be used to find the LCM of a set of numbers.
Therefore, the LCM of 7, 8, 14, and 21 is 168.
LCM and HCF Formula
In an alternate explanation, the formula for HCF and LCM establishes that the multiplication of any two numbers is equivalent to the product of their HCF and LCM. For further insights into the relationship between HCF and LCM, you can explore a page that delves into this connection.
The HCF and LCM formula finds applications in various scenarios. For instance, if one of the HCF or LCM values is known, the other can be readily determined without resorting to the methods discussed earlier. This concept is illustrated through an example.
Example: Given the HCF and LCM of two numbers as 8 and 96 respectively, with one of the numbers being 24, determine the other number.
Solution: Given: HCF = 8; LCM = 96; One number = 24; Second number = ?
Applying the HCF and LCM formulas allows us to deduce the unknown value.
HCF(a, b) × LCM(a, b) = a × b
Upon substituting the given values: 8 × 96 = 24 × b
Solving for 'b' yields: b = 768/24 = 32. Hence, the other number is 32.
Note: Similarly, the LCM of two numbers can be found if both numbers and the HCF are known, using the same formula.
LCM and HCF Formula Tricks
- When the HCF of two numbers is 1, their Least Common Multiple (LCM) will be equal to their product. For instance, if the HCF of 2 and 3 is 1, then the LCM of 2 and 3 will be 2 × 3 = 6.
- In the case of two coprime numbers, their HCF is invariably 1. For instance, consider the coprime numbers 4 and 5. Their HCF is 1 because coprime numbers possess no common factor apart from 1.
Difference between HCF and LCM
| HCF | LCM |
|---|---|
| The full form of HCF is Highest Common Factor. | The full form of LCM is the Least Common Multiple. |
| HCF is the largest of all the common factors of the given numbers. | LCM is the smallest of all the common multiples of the given numbers. |
| HCF of given numbers cannot be greater than any of them. | LCM of given numbers cannot be smaller than any of them. |
Properties of HCF And LCM
When the HCF of two numbers is 1, their Least Common Multiple (LCM) will be equal to their product. For instance, if the HCF of 2 and 3 is 1, then the LCM of 2 and 3 will be 2 × 3 = 6.
.In the case of two coprime numbers, their HCF is invariably 1. For instance, consider the coprime numbers 4 and 5. Their HCF is 1 because coprime numbers possess no common factor apart from 1
Definition of HCF and LCM
The Highest Common Factor (HCF), also referred to as the Greatest Common Divisor (GCD), is defined as follows:
HCF, an acronym for Highest Common Factor, pertains to the largest non-zero number that stands as the greatest among all shared factors of two or more given numbers. This value is also denoted as the Greatest Common Divisor (GCD).
| All the factors of 18 are 1, 2, 3, 6, 9, and 18 | All the factors of 21 are 1, 3, 7, and 21 |
| 1 ×18=18 2 × 9=18 3 × 6=18 | 1 × 21=21 7 × 3=21 |
The term LCM stands for Lowest Common Multiple or Least Common Multiple. The definition of LCM is as follows:
LCM, an abbreviation for Lowest or Least Common Multiple, denotes the smallest positive integer that can be evenly divided by all the provided numbers. For example, consider finding the LCM of 16 and 20. The LCM of 16 and 20 can be computed as 2 × 2 × 2 × 2 × 5, which results in 80. In this case, 80 represents the LCM of the numbers 16 and 20.
List of HCF and LCM Properties
The properties of HCF and LCM are notably useful for dividing items into smaller portions and for uniformly distributing sets of items into their largest possible groups. These properties offer intriguing insights into the relationships between HCF and LCM. Here are some significant properties of HCF and LCM:
- Multiplication Property: The product of the HCF and LCM of two numbers is equal to the product of those numbers. Mathematically, for numbers 'a' and 'b', HCF(a, b) × LCM(a, b) = a × b.
- Division Property: For two non-zero numbers 'a' and 'b', LCM(a, b) = (a × b) / HCF(a, b).
- Prime Factorization Property: When the prime factorization of a number is known, the HCF and LCM can be easily determined.
- Cancellation Property: If 'a' and 'b' are two numbers with a common factor 'c', then HCF(a, b) = HCF(a/c, b/c).
- Divisibility Property: If 'c' divides both 'a' and 'b', then 'c' also divides HCF(a, b).
Relation between HCF and LCM for Co-prime Numbers: When two numbers are coprime (have no common factors other than 1), their HCF is 1 and their LCM is the product of the numbers.
Important Notes
Certainly, here are the summarized properties of HCF and LCM:
HCF (Highest Common Factor) Properties:
- HCF of two or more numbers is the greatest among all the common factors they share.
- HCF is also known as the Greatest Common Divisor (GCD).
LCM (Least Common Multiple) Properties:
- LCM of two or more numbers is the smallest positive integer divisible by all the given numbers.
Properties of Co-prime Numbers:
Co-prime numbers have an HCF of 1, as they share no common factors other than 1.
The LCM of co-prime numbers is always equal to the product of the numbers.
These properties offer fundamental insights into the nature of HCF and LCM, making them valuable tools for various mathematical calculations and problem-solving scenarios.
LCM and HCF Formula FAQs
Define the terms HCF and LCM.
What are the methods used to find the LCM and HCF?
What is the relationship between HCF and LCM?
What are the properties of Co-prime?










