Change of Base Formula with Solved Examples

The Change of Base Formula , as its name implies, is a mathematical tool used to alter the base of a logarithm. Many scientific calculators provide buttons for "log" and "ln," representing logarithms with base 10 and base e (the natural logarithm), respectively. However, these calculators often lack the option to calculate logarithms with bases other than 10 and e.

The change of base formula addresses this limitation by allowing us to convert logarithms from one base to another, such as from e to 10 or from base 10 to e. It plays a crucial role in solving various logarithmic problems. Let's explore the change of base formula, its proof, and some solved examples to better understand its utility.

What Is Change of Base Formula?

The change of base formula is a mathematical technique employed to express a logarithm with a specific base as the ratio of two logarithms, both having the same base different from the original logarithm's base. This formula leverages the properties of logarithms and provides a way to compute logarithms with different bases. You can find the change of base formula as follows.

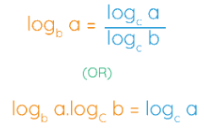
Change of Base Formula

The change of base formula can be expressed as follows. It involves changing the base of the given logarithm to a logarithm with a new base. Essentially, it transforms a single logarithm with a specific base into two logarithms with a new base while keeping the same argument. The formula for the change of base is as follows:

log_b(a) = [log_c(a)] / [log_c(b)]

In this formula:

The argument of the logarithm in the numerator (log_c(a)) is the same as the argument of the original logarithm (log_b(a)).

The argument of the logarithm in the denominator (log_c(b)) is the same as the base of the original logarithm (b).

The bases of both logarithms in the numerator and denominator should be the same, and this base can be any positive number other than 1.

Note: Another form of this formula, log_b(a) · log_c(b) = log_c(a), is also commonly used for problem-solving.

Also Check – Absolute Value Formula

Change of Base Formula Derivation

The derivation of the change of base formula can be understood through the following steps. Let's assume:

log_b(a) = p,

log_c(a) = q, and

log_c(b) = r.

By converting each of these logarithmic expressions into exponential form, we obtain:

a = b^p, a = c^q, and b = c^r.

From the first two equations, we have:

b^p = c^q.

Now, substituting b = c^r (which is derived from the third equation) into the previous equation, we get:

(c^r)^p = c^q.

Using a property of exponents, (am)^n = amn, we simplify it to:

c^(rp) = c^q.

Since the bases are the same, we equate the exponents:

rp = q.

Now, to solve for p, we divide both sides by r:

p = q / r.

Substituting the values of p, q, and r back into the original expression, we obtain the change of base formula:

log_b(a) = [log_c(a)] / [log_c(b)].

This formula allows us to change the base of a logarithm. Let's explore some applications of the change of base formula in the following section.

Also Read – Linear Equation Formula

Examples Using Change of Base Formula

Example 1: Calculate the value of log base 64 of 8 using the change of base formula.

Solution:

We will apply the change of base formula, changing the base to 10. Note that log base 10 is simply written as log.

log base 64 of 8 = [log 8] / [log 64]

= [log 8] / [log (8^2)]

= [log 8] / [2 log 8] [Using the property log_a(m) = m log_a]

= 1 / 2

Answer: log base 64 of 8 = 1 / 2.

Also Check – Rational Numbers Formulas

Example 2: Calculate log base 9 of 8 using a calculator. Round your answer to 4 decimal places.

Solution:

Since calculators typically don't have a button for log base 9, we first apply the change of base formula.

log base 9 of 8 = [log 8] / [log 9]

≈ [0.903089...] / [0.95424...]

≈ 0.9464

Answer: log base 9 of 8 ≈ 0.9464.

Example 3: Evaluate the expression log base 3 of 2 times log base 4 of 3 times log base 5 of 4.

Solution:

Using the alternate form of the change of base formula, log_a(b) * log_b(c) = log_a(c), we apply it twice to evaluate the given expression.

log base 3 of 2 * log base 4 of 3 * log base 5 of 4

= log base 4 of 2 * log base 5 of 4

= log base 5 of 2

Answer: log base 3 of 2 * log base 4 of 3 * log base 5 of 4 = log base 5 of 2.