Linear Equation Formula
A linear equation is an equation in which the degree of the variable is always equal to 1. It is also known as a one-degree equation or linear equation. The general form of a linear equation in one variable is given as Ax + B = 0.
Where x is a variable that keeps on, varying depending on the question need. From the general form, we have A as a coefficient and B as a constant.
The standard form of a linear equation in two variables is of the form Ax + By = C. Here, x and y are variables, A and B are coefficients and C is a constant.
What is a Linear Equation?
An equation that consists of the highest power of 1 is known as a
linear equation
. This means that in a given equation there will be no variable whose exponent is more than 1. The graphical representation of a linear equation always is a straight line.
Linear Equation Definition:
A linear equation is one of the types of algebraic equations in which each term of the equation has a power of 1 and whenever we draw the graph of a linear equation it results in a straight line. That’s why many times the linear equation is termed a straight-line equation.
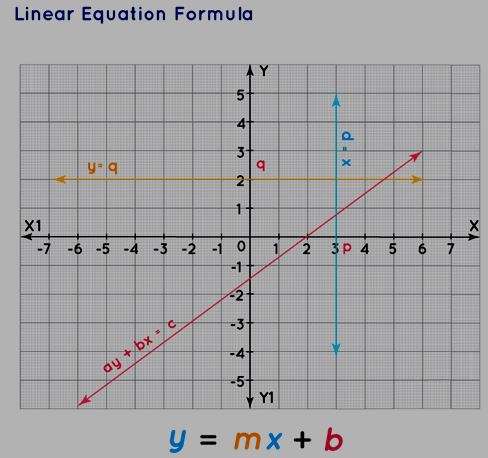
Linear Equation Formula
The linear equation formula is one of the ways of representing a linear equation. This can be done in various ways. Such as a linear equation can be represented in the standard form, the slope-intercept form, and the point-slope form.
Firstly, we discuss the standard form of a linear equation, So, let’s learn how we can express the given linear equation. We can see a variety of differences that exist from case to case depending on the number of variables and the most important thing to keep in mind is that the highest (and the only) power of all existing should be equal to 1 for all the linear equations.
-
Slope intercept form of a linear equation is y = mx + c (where m = slope and c = y-intercept)
-
Point slope form of a linear equation is y – y
1
= m(x – x
1
) (where m = slope and (x
1
, y
1
) is a point on the line)
IMPORTANT:
The slope-intercept form of a linear equation tells us the amount by which the line is moving upward and moving downwards. It is measured by the formula moving upward / moving downwards. i.e., if (x
1
, y
1
) and (x
2
, y
2
) are any two points on a line then
its slope is calculated using the formula
(y
2
- y
1
)/(x
2
- x
1
).
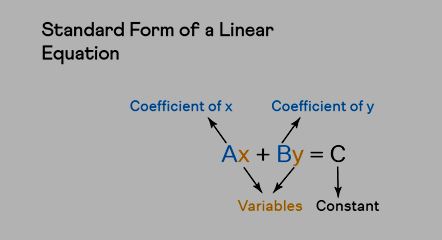
Linear Equations in Standard Form
The standard form or we can say the general form of linear equations in one variable is of the form,
Ax + B = 0;
where A and B are real numbers, and x is the variable.
The
general form of
two variables is expressed as,
Ax + By = C;
where A, B, and C are any real numbers, and x and y are the variables.
Also Read - Absolute Value Formula
Linear Equation Graph
The
graphical representation of a given linear equation
in one variable forms a straight line that is parallel to the y-axis and vice-versa, On the other hand, the graph of a linear equation in two variables forms a straight line due to this reason it is also known as straight line equations. The graphical representation of a linear equation is given below.
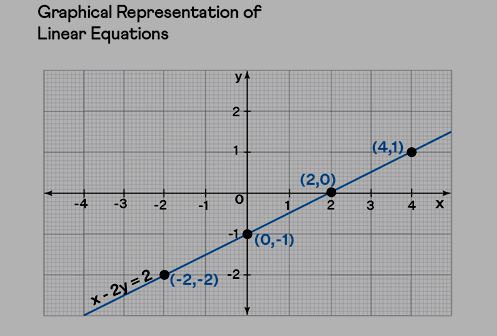
Linear Equations in One Variable
A linear equation with one variable is one that contains just one variable. It has the form Ax + B = 0, with A and B being any two real numbers and x being an ambiguous variable with only one possible value. The simplest approach to represent a mathematical statement is in this way. The degree in this equation is always equal to one. One-variable linear equations are fairly simple to solve. To determine the value of the unknown variable, the variables are divided and placed on one side of the equation, and the constants are combined and placed on the other side.
Linear Equations in Two Variables
A linear equation with two variables has the formula Ax + By + C = 0, where A, B, and C are all real numbers and x and y are the two variables with degrees of 1 each. Such two linear equations are referred to as simultaneous linear equations. For instance, the linear equation 4x + 3y + 8 = 0 has two variables. The graphical approach, the substitution method, the cross-multiplication method, the elimination method, and the determinant method are only a few of the ways to solve linear equations in two variables.
How to Solve Linear Equations?
A mathematical equation resembles a balance scale with identical weights on either side. An equation remains valid even if the same integer is added to or subtracted from both sides. Similarly, to this, an equation is accurate if the same integer is multiplied or divided on both sides. We place the constant on one side of the equation, and the variables on the other, and then we calculate the value of the unknown variable. This is how a linear equation with a single variable is solved.
Points to Remember regarding Linear Equations:
-
The value of the variable that makes the linear equation true is called the solution or root of the linear equation.
-
The solution of a linear equation is not affected by adding, subtracting, multiplying, or dividing the same number to both sides of the equation.
-
The graph of a linear equation in one or two variables always forms a straight line.
