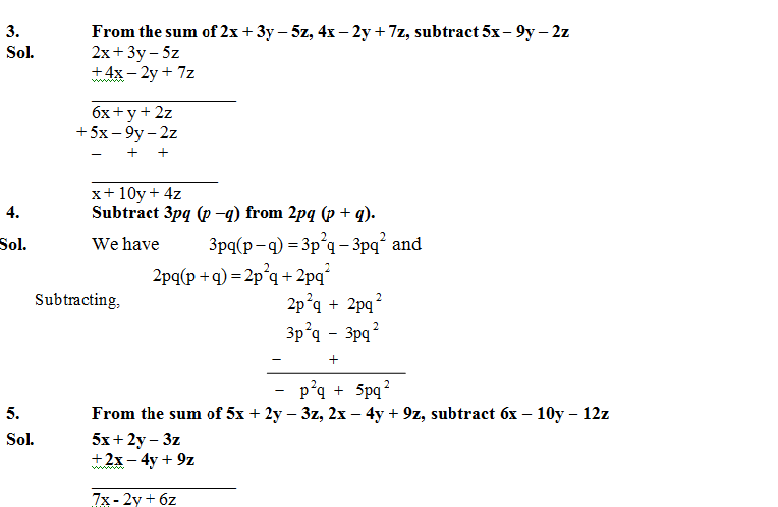Subtraction

1. Any quantity b is said to be subtracted from any other quantities a, when a third quantity c is found such that the sum of b and c is equal to a. In other words c = a – b. When c is such that a = b + c, a is called minuend, b is called subtrahend and c is called the remainder.

2. Subtraction of like terms can be performed in a manner exactly similarly to that used in subtraction of integers. For any 2 integers a and b we have a – b = a + (additive inverse of b). Change the sign of term to be subtracted and add the new monomial to the one from which subtraction is to be made.

E.g.: (+7a) – (+ 3a) = + 7a + (– 3a) = + 4a

(– 8a) – (– 2a) = (– 8a) + (+ 2a) = – 6a

Column method for subtraction of Algebraic expressions:

Write the expression to be subtracted below the other expression such that like terms of the two expressions are in the same column. Now change the sign of each term of lower expression and add term wise

Horizontal method for subtraction of Algebraic expressions:

Change the sign of each term of the expression to be subtracted and then add