Collision Theory Of Reaction Rates

According to collision theory, a reaction takes place because the molecules collide with each other. The number of collision that takes place per second per unit volume of the reaction mix is called collision frequency. At ordinary temperature and pressure the value of collision frequency is so high ( 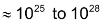in a gaseous reaction) that if all the collisions were effective, the reaction should be completed in fraction of seconds. However, in actual practice, that is not so. This is explained on the basis of two factors.

(i) Energy factor

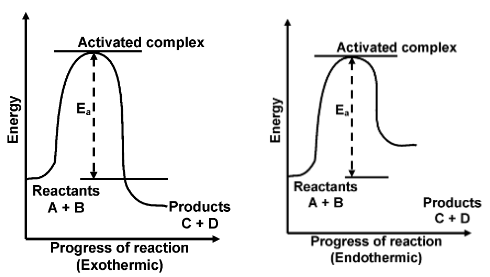
For a collisions to be effective, the colliding molecules must have energy more than a particular value. The minimum energy which the colliding molecules must have in order that the collision between them may be effective is called threshold energy. Thus at ordinary temperature and pressure, most of the molecules may not posses energy equal to or greater than threshold value.

A collision between high energy molecules overcomes the repulsion and bring the formation of an unstable molecule cluster, called the activated complex.

Thus, every chemical reaction whether exothermic or endothermic has an energy barrier which has to be overcome before reactants can be transformed into products. If the reactant molecules have sufficient energy, they can reach the peak of the energy barrier after collision and then they change into products. If the activation energy for a reaction is low, the fraction of effective collisions will be large and reaction will be fast. On the other hand, if the activation energy is high, then fraction of effective collisions will be small and the reaction will be slow. When temperature is increased, the number of active molecules increases, i.e., the number of effective collisions will increase and the rate of reaction will increase.

Activation energy Ea = E(activated complex) – E(ground state)

ΔH = activation energy of forward reaction − activation energy of backward reaction.

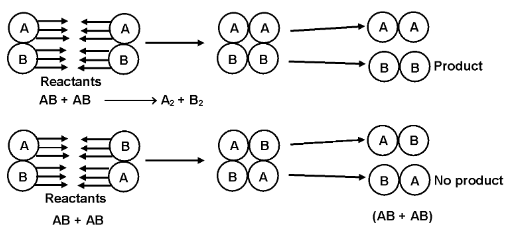
(ii) Orientation factor

In some cases it is found that even if a larger number of colliding molecules have energy more than threshold value, still the reaction is slow. This is because of improper orientation of the colliding molecules at the time of collisions.

Rate of reaction is directly proportional to the number of effective collisions.

Rate =

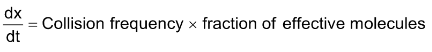
= z × f

According to kinetic theory of gases, the fraction of molecules having energy more than a particular value, E at temperature T is given by

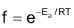
Rate =

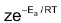
As rate of reaction is directly related to rate constant K, we can also write

K =

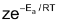
Arrhenius Equation

The variation of equilibrium constant of a reaction with temperature is described by Van’t Hoff equation of thermodynamics which is as follows:

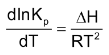
If k1 and k ₂ be the rate constants of forward reaction and backward reaction, respectively then Kp = k ₁ /k ₂ . Further,
ΔH = Ea ₁ – Ea ₂ .Putting these in the above equation we get,

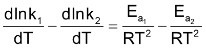
Splitting into two parts

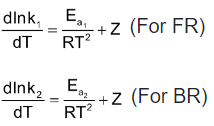
where Z is constant

Arrhenius sets Z equal to zero and without specifying FR and BR, he gave the following equation called Arrhenius equation.

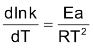…(i)

From this equation it is evident that rate of change of logarithm of rate constant with temperature depends upon the magnitude of energy of activation of the reaction. Higher the Ea smaller the rate of change of logarithm of rate constant with temperature. That is, rate of the reaction with low Ea increases slowly with temperature while rate of the reaction with high Ea increases rapidly with temperature. It is also evident that rate of increase of logarithm of rate constant will go on decreasing with increase of temperature.

Integrating Equation 4 assuming Ea to be constant we get,

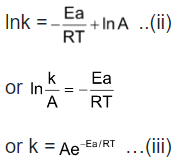
Equation (iii) is integrated form of Arrhenius equation. The constant A called pre-exponential factor is the frequency factor since it is somewhat related with collision frequency. It is a constant for a given reaction. From Equation (iii) it is evident that as T → ∞, k → A. Thus, the constant A is the rate constant of reaction at infinity temperature. The rate constant goes on increasing with temperature.

So, when T approaches infinity, k will be maximum. That is to say, A is the maximum rate constant of a reaction.

It is also to be noted that the exponential term i.e. e–Ea/RT measures the fraction of total number of molecules in the activated state or fraction of the total number of effective collisions. If nEa and n be the number of molecules of reactant in the activated state and the total number of molecules of the reactant present in the reaction vessel respectively, then

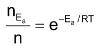
Equation (ii) may also be put as

logk = 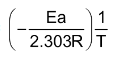+ logA …(iv)

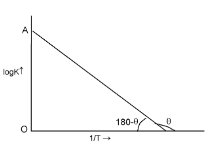
Since 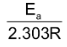and logA both are constants for a given reaction. So from equation (iv) it is evident that a plot of log k vs. 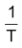will be a straight line of the slope equal to and intercept equal to logA as shown below.

Thus, from this plot Ea and A both can be determined accurately.

If k1 be the rate constant of a reaction at two different temperature T1 and T2 respectively then from equation (iv), we may write

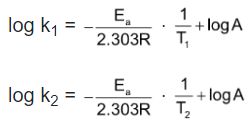
Subtracting former from the latter we get

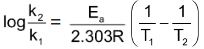… (v)

With the help of this equation it is possible to calculate Ea of a reaction provided, rate constants of reaction at two different temperatures are known. Alternatively one can calculate rate constant of a reaction at a given temperature provided that rate constant of the reaction at some other temperature and also Ea of the reaction is known.