Self Inductance

It is convenient to express the induced emf in terms of the current in a circuit rather than the magnetic flux through it. If no magnetic materials are present, the magnetic field produced by a coil, and hence also the flux, are directly proportional to the current flowing through it,

Thus,Φ = L I

Where L is a constant of proportionality called the self-inductance of the coil. Its SI unit is henry (H). The self-inductance of a circuit depends on the size and shape.

Using Faraday's law the induced emf in the coil is given by

ε = 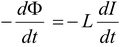(4.11)

The polarity of the emf depends on the rate of change of the current, not on its magnitude or its direction. This is illustrated in Fig. 4.18.

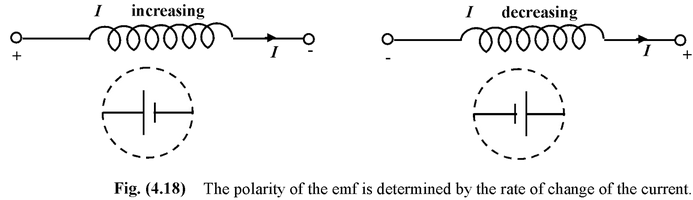
Self-inductance of a solenoid

To a good approximation, the magnetic field inside the solenoid is uniform and given by

B = µ0

where n = N/ l is the number of turns per unit length, N the total number of turns, l the total length, and I the current in the solenoid.

The flux through the solenoid is

Φ = BNA = µ _0n INA =

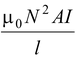
As expected, the flux is proportional to the current I. The proportionality constant is the
self-inductance.

L = 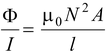(4.12)

Example: 4.7

Find the self inductance of a solenoid of length 10 cm, area 5 cm2 and number of turns 100.

Solution

We know L =

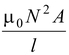
Here µ0 = 4π × 10 ^-7 H/m; N = 100 ; A = 5 × 10 ^-4 m ² ; l = 0.1 m

∴L = 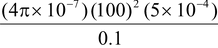= 2π × 10 ^-5 H