Capacitors
Electrostatics of Class 12
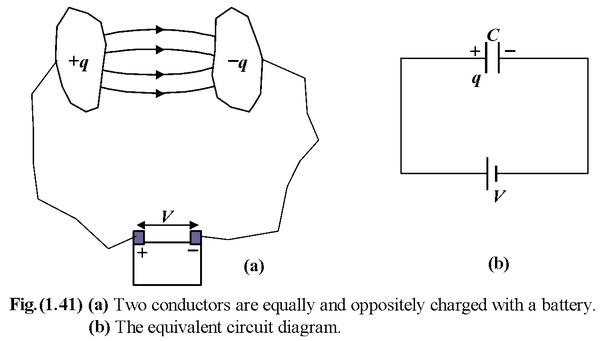
A capacitor is a device that stores electrical energy. It consists of two conducting plates separated by an insulator. If the plates carry charges ±q and have a potential difference V, the capacitance of the capacitor is defined as the magnitude of the charge on one plate divided by the magnitude of the potential difference V between them
C = q/v (1.30)
Capacitance depends on the size and shape of the plates and the material between them. It does not depend on q or V individually. The SI unit of capacitance is the farad (F).
1 farad = 1 coulomb/volt
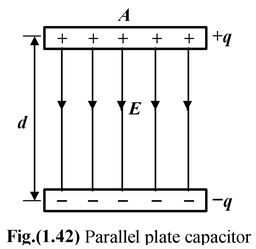
Parallel Plate Capacitor
|
σ = q/A
E =
V = Ed =
C =
|
|
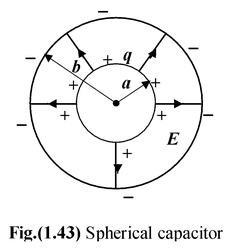
Spherical Capacitor
V =
∴ C =
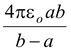 (1.32)
(1.32)
|
|
If the radius of the outer sphere tends to infinity b → ∞, the capacitance reduces to
C = 4πεoa
which is called the capacitance of an isolated sphere
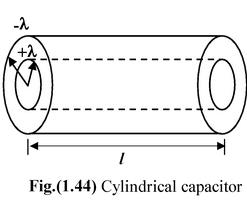
Cylindrical Capacitor
E =
|
|
|
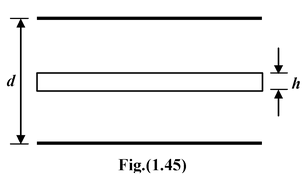
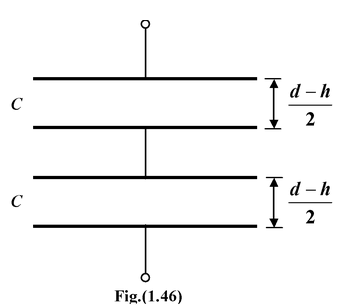
Example 1.17 A parallel plate capacitor has plates of area A separated by a distance d. A metal block of thickness h is inserted midway between the plates, as shown in the figure (1.45). Find the capacitance of the system. |
|
||
|
Solution The system can be idealized as shown in the fig. (1.46). It is a system of two capacitors in series. The capacitance of each capacitor is given by
C =
The equivalent capacitance is
Ceq =
|
|
||
Does the capacitance change if the block is moved so that it touches one of the plates ?
|
Example: 1.18 The Fig. (1.47 a) shown a system of parallel conductors. Each plate is of equal area A and equally separated by d. Find the equivalent capacitance of the system between a and b. |
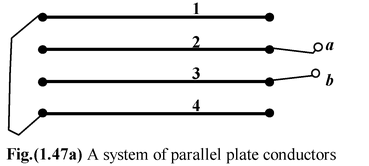
|
Solution
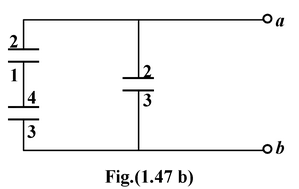
By joining the points of same potential, the arrangement of conductors may be reduced as shown in the fig. (1. 47 b).
|
If the capacitance between two successive plates is given by
C =
then, the equivalent capacitance of the system is given by
Ceq =
|
|
Energy stored in a Capacitor
The energy stored in a capacitor is equal to the work done to charge it. Let q be the instantaneous charge on either plate of the capacitor and the potential difference between the plates is V = q/C. The work done to transfer an infinitesimal charge dq from the negative plate to the positive plate is
dW = Vdq = (q/C)dq
The charge moves through the wires, not across the gap between the plates.
The total work done to transfer charge Q is
W =
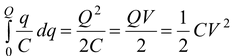 (1.34)
(1.34)
Since the charge on each plate is unaffected the capacitance in the presence of the dielectric is
C =
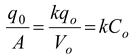
The capacitance of the capacitor increases by a factor k.
Where is the Potential Energy stored ?
The energy is stored in the space occupied by the electric field. In the case of parallel plate capacitor electric field is confined in the spacing between the plates.
C =
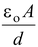 and V = Ed
and V = Ed
∴ U = 1/2CV² = 1/2
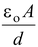 (Ed)2 =1/2εoE2 (Ad)
(Ed)2 =1/2εoE2 (Ad)
Since volume between the plates where the field exists is Ad, the energy density or the energy per unit volume is
u =
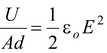 (1.35)
(1.35)
Example: 1.19
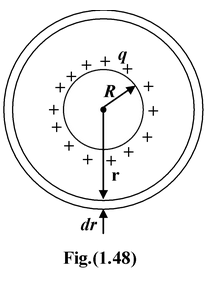
A charge q is uniformly distributed over a conducting sphere of radius R. Find the energy stored by the sphere in the surrounding space.
Solution
Consider a concentric shell of radius r and thickness dr as shown in the fig. (1.48).
Using equation (1.35) the energy stored in unit volume is given by
u = 1/2εoE 2
|
Applying Gauss Law, electric fields at a distance r from the centre of the sphere is
E =
Energy stored in shell of radius r and thickness dr is dU = 1/2εo E 2 (4πr 2 dr)
or
dU = 1/2 εo
|
|
dU =
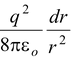
The total energy stored can be obtained by integrating the above expression from R to ∞.
U =
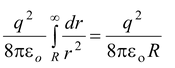
Note that the energy stored can also obtained by U = q 2 /2c

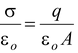
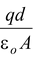
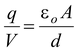 (1.31)
(1.31)
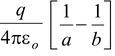 from equation (1.25)
from equation (1.25)
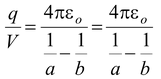
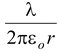 a ≤ r ≤ b
a ≤ r ≤ b
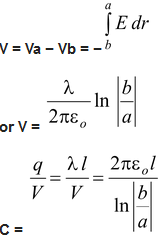
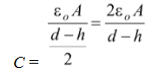
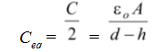
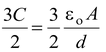
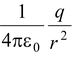
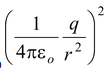 (4πr
2
dr)
(4πr
2
dr)