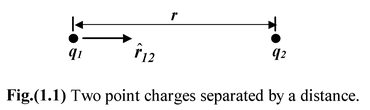Coulomb’s Law
Share
Coulomb’s Law
Electrostatics of Class 12
COULOMB’S LAW
The force of interaction of two stationary point charges in vacuum is directly proportional to the product of these charges and inversely proportional to the square of their separation
F = kq 1 q 2 /r 2 (1.1)
where k is a constant which depends on the system of units. Its value in SI unit is
k = 9 × 109 Nm2C-2
The constant is often written in the form
k = 1/4πε 0
where ε0 is called the permitivity constant which is numerically equal to
εo = 8.85 × 10−12 C2 /Nm2
|
The coulomb force acts along the straight line joining the points of location of the charges. This force is central and spherically symmetric. The vector form of Coulomb’s law is |
|
F 12 = (kq 1 q 2 /r2) r 12 (1.2)
where r 12 is the unit vector, directed from q1 to q2 and F 12 is the force on the charge q1 due to q2. Similarly force on charge q2 due to q1 is F 21 .
F 21 = (kq 1 q 2 /r2) (-r 12 )
Important points regarding Coulomb’s law
1.Charges are assumed to be at rest.
When charges are in motion they also produce and experience magnetic forces.
|
2.Charges are assumed to be on point particles. Coulomb’s law cannot be applied directly to a finite charge distribution. There is an exception: when the charge is distributed uniformly over a spherical surface, the force on a point charge outside the surface may be computed from Coulomb’s law by treating the charge on the sphere as if it were concentrated at the centre. For charged body of finite size, there is no well−defined value of the separation r, integration is required. |
|
Principle of Superposition
|
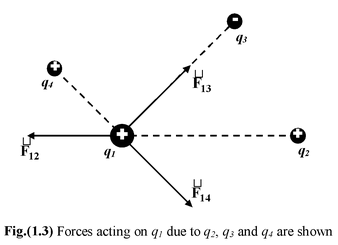
The coulomb’s law obeys the principle of superposition, which means that the force between two particles is not affected by the presence of other charges. This principle is used to find the net force exerted on a given particle by other charged particles. The net force F 1 on q1 is simply the vector sum F 1 = F 12 + F 13 + F 14 Note that the notation F 12 represents the force on q1 due to q2. |
|
How to solve a problem using Coulomb’s law ?
1.Decide whether the force due to a given charge is attractive or repulsive and express it by drawing vectors.
2.Find the magnitude of the force using Coulomb’s law − ignoring the signs of the charges.
3.Resolve the forces along the given co−ordinate axes and express them in vector form using i, j ,k unit vector notation unless otherwise specified.
4.Use the principle of superposition to find the net force on a charge.
Example: 1.1
|
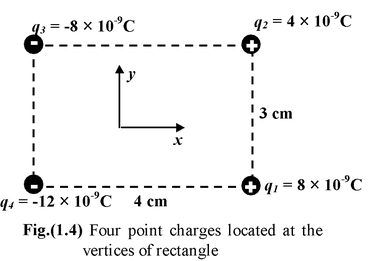
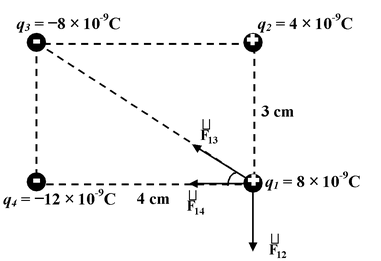
Four point charges are located at the corners of a rectangle as shown in the figure. Find the net force acting on the charge q1. |
|
|
|
Solution 1.The force F 12 (between q1 and q2 is repulsive while the forces F 13 (between q1 and q3) and F 14 (between q1 and q4) are attractive. 2.The magnitude of the forces F 12 , F 13 , F 14 are |
|
|
F12 =
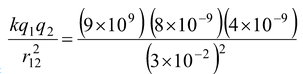= 32 × 10−5 N
F13 =
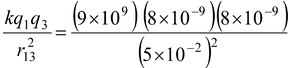= 23 × 10−5 N
F14 =
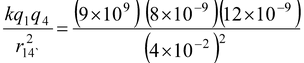= 54 × 10−5 N
3. F12 = −(32 ×10−5)j
F13 = −(F13cosθ)i + (F13 sinθ)j =
= 10−5 [−18.4 i + 13.8 j]
F14 = −(54 × 10−5) i
4.The net force on q1 is
F1 = F12 + F13 + F14
F1 = 10−5 [−72.4i − 18.2j] N
