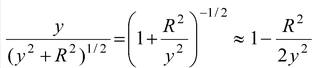Electric Field
Electrostatics of Class 12
ELECTRIC FIELD
How does one charge exerts force on the other ?
An electric charge influences its surroundings by creating an electric field. The second charge does not interact directly with the first, rather, it responds to whatever field it encounters.
The electric field strength (E) at a point is defined as the force per unit charge experienced by a test charge qt, placed at that point.
E= F/q t (1.3)
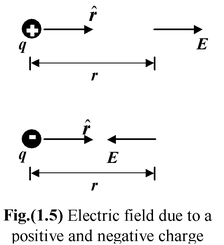
The direction of E is that of the force on a positive charge. In other words, positive charges experience forces parallel to the field, and negative charges experience forces opposite to the field Once the field strength is known, the force on any charge q can be found from
F = qE(1.4)
|
From Coulomb’s law, the electric field created by a point charges q is given by E = kq/r 2 (r)(1.5) where the unit vector r has it's origin at the source charge q. The electric field due to a charge points away from the charge if it is positive and toward it if the charge is negative. |
|
|
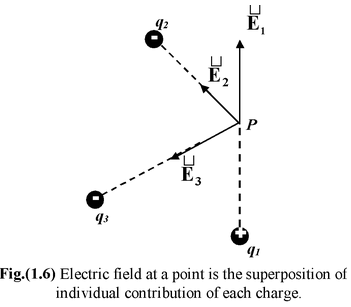
Principle of superpositionSince the principle of superposition is valid for Coulomb’s law, it is also valid for the electric field. To calculate the field strength at point due to a system of charges, we first find the individual field intensity E1 due to q1, E2 due to q2 and so on. For N point charges, the resultant field intensity is the vector sum E = E1 +E2 + …….. + EN= ΣEi(1.6) |
|
|
How to find electric field intensity at a point?
1.First draw the field vectors at the given location. Their directions can be found by assuming that there is a positive charge at that point.
2.Find the magnitude of the field intensity due to each charge using Coulomb’s law
E = kq/r 2
3.Place the origin at the point at which E is being calculated. The choice of co−ordinate axes determines the signs of the components of the field intensity E.
4.Use the principle of superposition to find resultant intensity at that point.
|
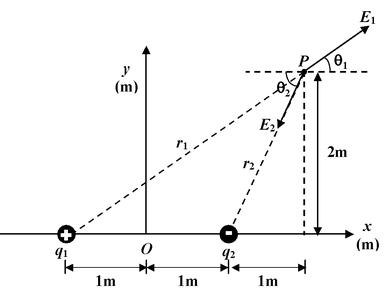
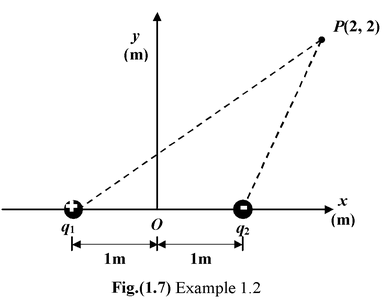
Example: 1.2 The figure shows a system of two charges. A point charge q1 = 20 nC is at (−1,0) while q2 = −10 nC is at (+1,0). Find the resultant field intensity at a point P with coordinates (2, 2). Solution 1.The field vector E1 points away from the charge q1 while the vector E2 points toward the charge q2. |
|
2.The distances r1 and r2 are
r1 = √(2 + 1) 2 + 2 2 = √13 = 3.6m
r2 = √1 2 + 2 2 = √5 = 2.2 m
The magnitude of the fields are
E1 =
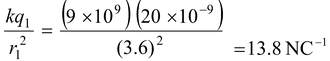
E2 =
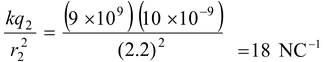
3.The components of the resultant field are
Ex = E1 cos θ1 − E2 cos θ2
Ey = E1 sin θ1 − E2 sin θ2
wherecos θ1 = 3/6.6; cos θ2 = 1/2.2
andsin θ1 = 2/3.6 ; sin θ2 = 2/2.2
Thus,Ex = (13.8) 3/3.6 - 18 (1/2.2) = 3.3 NC−1
Ey = (13.8) 2/3.6 − 18 (2/2.2) = −8.7 NC−1
Finally, E = 3.3 i − 8.7 j NC−1
Continuous Charge Distribution
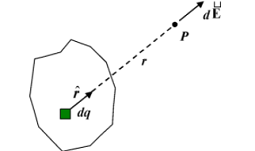
To find the electric field due to a continuous distribution of charge, we divide the charge distribution into infinitesimal elements of charge dq which may be considered to be point charges. The infinitesimal contribution of the total field produced by such an element is
|
dE = kdq/r 2 (r) (1.7) where r has its origin at the charge element. The total field is the sum (integral) of all such contributions over the charge distribution. E = k∫dq/r2 r |
|
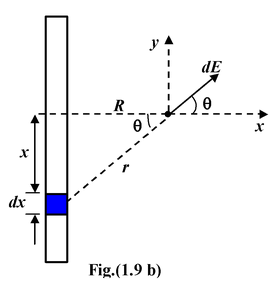
Example: 1.3
|
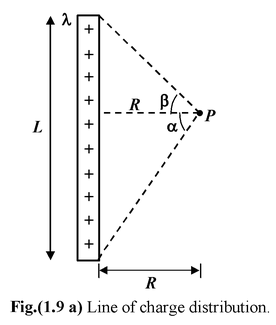
Find the field intensity at a distance R from a finite line of charge of length L and linear charge density λ C/m, as shown in the figure. Solution Consider a small element of length dx at a distance x, as shown in the figure. The magnitude of the contribution to the field at point P from this element is dE = kλdx/r 2 (i) To carry out the integration we express the variables in terms of the angle θ, From the figure, r = R sec θ andx = R tan θ on differentiating, dx = R sec2 θ dθ |
|
|
Using these expression (i) may be modified as
dE =
The components of dE are dEx = dE cos θ; dEy = dE sin θ On integrating
Ex =
=
|
|
Ey =
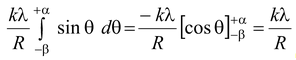 (cos β − cos α)
(cos β − cos α)
For an infinite line of charge , α = π/2 and β = π/2
Therefore, Ex = 2kλ/R and Ey = 0
∴
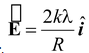
Notice that the field due to a line charge distribution decreases as 1/R and it never reduces to 1/R2, (behaviour of a point charge).
Example 1.4
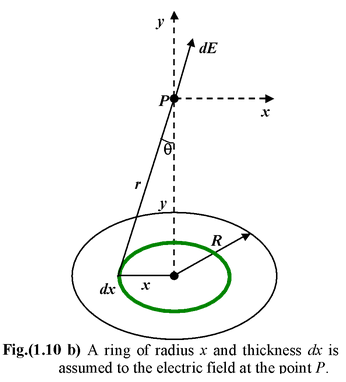
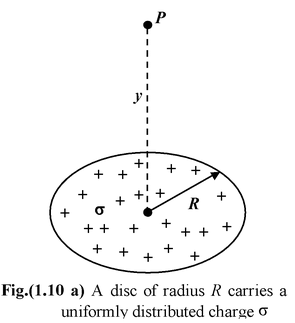
Find the field intensity at a distance y from the centre along the central axis of a circular disc of radius R and surface charge density σ(C/m2).
|
Solution Due to circular symmetry of the disc, a ring of radius x and width dx is chosen. All points of the ring are equidistant from the point P. Consider a component of the field parallel to the plane of the disc. Any contribution of this component from some point on the ring has an equal and opposite contribution from the diametrically opposite part of the ring. Thus, due to symmetry, there is no component of the field parallel to the plane of the disc i.e.Ex = 0 The y−component of the field is dEy = dE cos θ = kdq/r2 y/r |
|
where dq = σ dA = σ(2πx dx)
|
andr2 = x2 + y2
∴dEy =
On integrating
Ey = πkσy
or Ey = 2πkσ
Note ∙When y >> R, using binomial theorem.
Thus, the expression reduces to |
|
Ey = πkσR 2 /y 2
or Ey = kq/y 2 since q = σ(πR2)
Which represents the electric field due to a point charge
∙As R → ∞, the disc behaves like an infinite sheet and the expression (i) reduces to
E = 2πkσ = σ/2εo

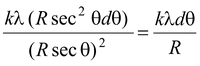
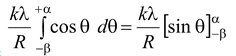
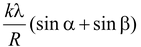
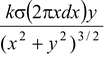
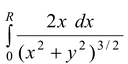
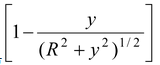 (i)
(i)