Some Important Terms Related To Spherical Mirrors
Light of Class 9
SOME IMPORTANT TERMS RELATED TO SPHERICAL MIRRORS
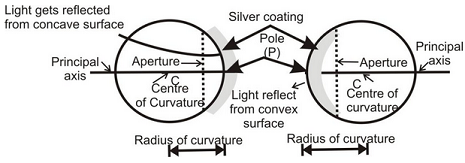
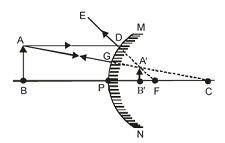
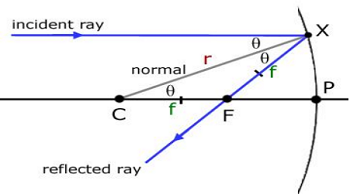
CENTRE OF CURVATURE (C):
The center of the circle whose center lies on the concave side of a curve on the normal to a given point of the curve and whose radius is equal to theradius of curvatureat that point .The centre of curvature of a spherical mirror is the centre of the imaginary hollow sphere of glass, of which the spherical mirror is a part. The centre of curvature is usually denoted by the letter C. The centre of curvature of a concave mirror is in front of it and the centre of curvature of convex mirror is behind the mirrors as shown in the figure.
RADIUS OF CURVATURE (R):
The radius of curvature of a spherical mirror is the radius of the imaginary hollow sphere of glass, of which the spherical mirror is a part. The radius of curvature is usually denoted by the letter ‘R’.
In figure above the distance PC is the radius of curvature of a concave mirror and the distance PC is the radius of curvature of a convex mirror.
POLE (P):
The centre of the reflecting surface of a spherical mirror is called its pole. It is usually denoted by the letter ‘P’ in each concave and convex mirror. The pole of a spherical mirror lies on the surface of the mirror.
PRINCIPAL AXIS:
The principal axis of a spherical mirror is the straight line passing through the centre of curvature C and pole P of a spherical mirror, produced on both sides.
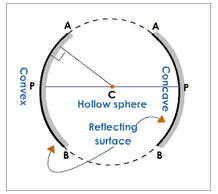
APERTURE:
The portion of a mirror from which the reflection of light actually takes place is called the aperture of the mirror. It is also called linear aperture of the mirror. The aperture of a spherical mirror is denoted by the diameter of its reflecting surface.
FOCAL PLANE:
A plane passing through the principal focus and at right angles to the principal axis of a spherical mirror is called its focal plane.
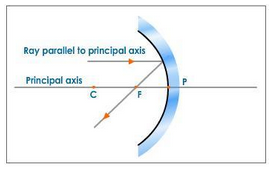
FOCAL LENGTH:
The distance between the pole and the focus is called the focal length. The focal length is half the radius of curvature.
PRINCIPAL FOCUS:
|
Focus of concave mirror |
Focus of convex mirror |
|
A parallel beam of light after reflectioin from a concave mirror converges at a point in front of the mirror. This point (F) is the focus of a concave mirror it is real. |
A parallel beam of light after reflectioin from a convex surface diverges and the rays do not meet. However on producing backward, the rays appear to meet at a point behind the mirror. This point is focus of the convex mirror and it is virtual. |
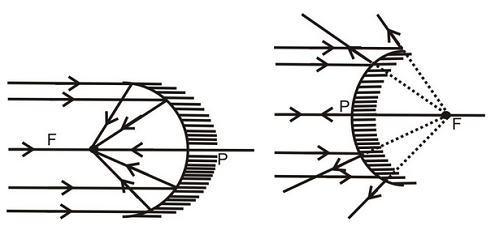
RELATION BETWEEN RADIUS OF CURVATURE AND FOCAL LENGTH OF A SPHERICAL MIRROR:
For spherical mirror having small aperture, the principal focus ‘F’ lies exactly at the mid point of the pole P and the centre of curvature C as shown in the figure 12 & 13. Therefore the focal length of a spherical mirror (concave or convex) is equal to half of its radius of curvature.
i.e. f = R/2 ⇒ R = 2f
CONCAVE AND CONVEX MIRROR:
Convex mirror is a spherical mirror, whose inner (cave type) surface is silvered and reflection takes place at the outer (convex) surface.
Concave mirror is a spherical mirror, whose outer bulged surface is silvered and reflection takes place from the inner hollow (cave type) surface.
Rules for the formation of images by concave & convex mirrors:
(i) A ray incident parallel to the principal axis actually passes (concave) or appears to pass (convex) through the focus.
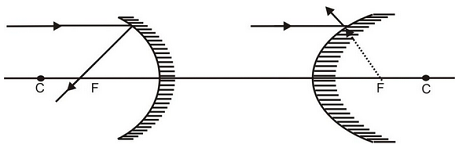
Concave Convex
(ii) A ray incident through the centre of curvature (C) falls normally and is reflected back along the same path.
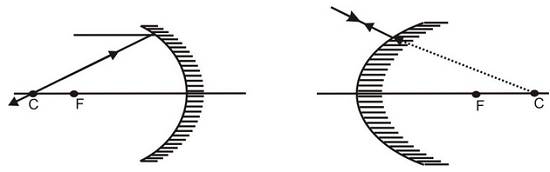
Concave Convex
(iii) A ray incident through the focus is reflected parallel to the principal axis.
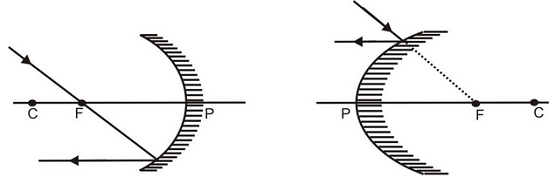
Concave Convex

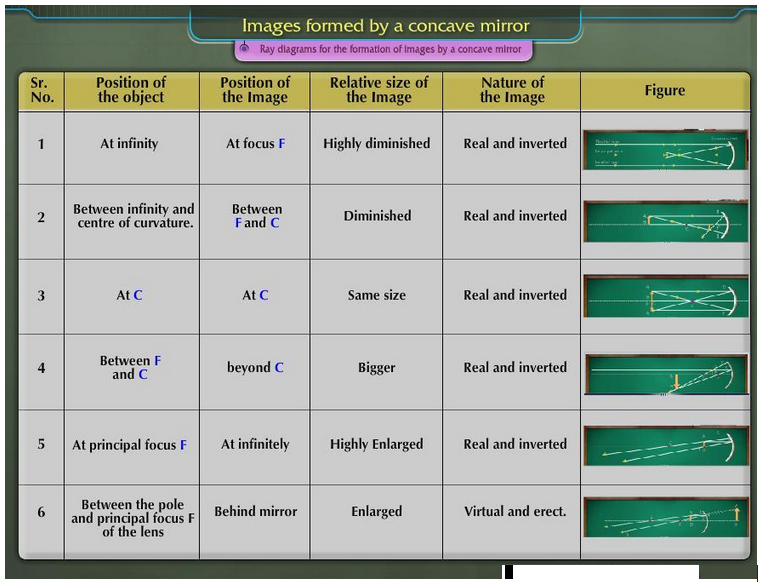
FORMATION OF DIFFERENT TYPES OF IMAGES BY A CONCAVE MIRROR IN DIFFERENT POSITIONS OF THE OBJECT:
The type of image formed by a concave mirror primarily depends on the position of the object in front of the mirror. When an object is moved closer to the mirror, starting from infinity, the following six cases arise:
Formation of Image by a concave mirror:-
Formation of image depends upon the position of the object. There are six possibilities of the position of object in the case of concave mirror.
- Object at infinity
- Object between infinity and centre of curvature (C)
- Object at centre of curvature (C)
- Object between centre of curvature (C) and Principal focus (F)
- Object at Principal Focus (F)
- Object between Principal Focus (F) and Pole (P)
(i) When the object is at infinity
When the object is at infinity, the rays of light starting from the object on travelling such a large distance are assumed to become parallel to each other while falling on the mirror. These parallel rays of light may fall on the mirror in the following two ways.
In the above two cases image is formed at the focus of the mirror. Therefore we can say that when the object is at infinity. The image is:
- Formed at the focus ‘F’ of the mirror.
- Real and inverted.
- Highly diminished, point sized.
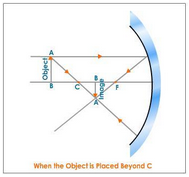
(ii) When the object is beyond the centre of curvature ‘C’ of concave mirror
When the object is placed beyond the centre of curvature ‘C’ of the concave mirror, the image is.
- Formed between the Focus ‘F’ and the centre of curvature ‘C’ of the concave mirror
- Real and inverted.
- Smaller in size and diminished.
|
|
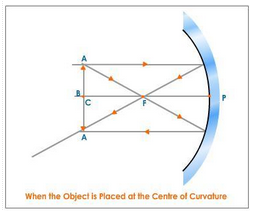
(iii) When the object is at the centre of curvature of concave mirror
When the object is placed at the centre of curvature of concave mirror. The image is
- Formed at the centre of curvature ‘C’ of the concave mirror.
- Real and inverted.
- Of the same size as that of the object.
|
|
|
(iv) When the object is placed between the centre of curvature ‘C’ and Focus ‘F’ of concave mirror
When the object is placed between the centre of curvature ‘C’ and Focus ‘F’ of concave mirror. The image is: Ray diagrams are useful tools for determining the location of an image as produced by a concave mirror. To determine the location of an image using a ray diagram, at least two sets of incident and reflected rays must be constructed for strategic positions on the object. The image of an object is the location where light rays from that object intersect upon reflecting from a mirror. By constructing at least two sets of incident and reflected rays, this image location can easily be found.
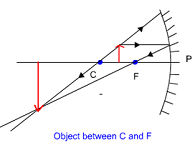
- (Formed beyond centre of curvature ‘C’ of concave mirror
- Real and inverted.
- Enlarged, i.e. Larger in size than the object.
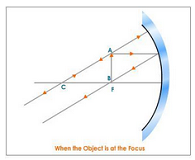
(v) When the object is at the Focus ‘F’ of a concave mirror
When the object is placed at the focus ‘F’ of a concave mirror. The image is
- Formed at infinity.
- Real and inverted.
- Highly enlarged, magnified.
|
|
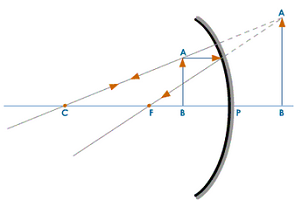
(vi) When the object is placed between Focus ‘F’ and pole ‘P’ of the concave mirror
When the object is placed between the Focus ‘F’ and Pole ‘P’ of the concave mirror as shown in the. The image is
- Formed behind the mirror.
- Virtual and erect.
- Enlarged, larger than the size of the object.
|
|
Image formation by a concave mirror for different positions of the object:
USES OF CONCAVE MIRROR:
- They are used as shaving mirrors.
- They are used as reflectors in car head-lights, search lights, torches and table lamps.
- They are used by doctors to concentrate light on body parts like ears and eyes which are to be examined.
- Large concave mirrors are used in the field of solar energy to focus sun-rays on the objects to the heated.
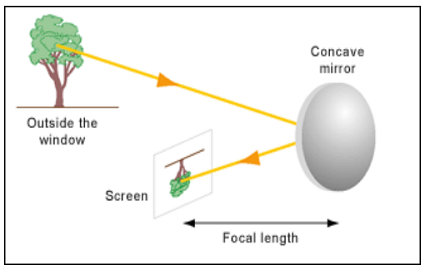
METHOD TO FIND OUT THE APPROXIMATE FOCAL LENGTH OF A CONCAVE MIRROR:
Determining the Focal Length of a Concave Mirror
Conditions
A beam of light incident parallel to the principal axis, after reflection from the sphericalmirror, eitheractually converges to or appears to diverge from afixed pointon the principal axis. Thisfixed pointon the principal axis of the spherical mirror is called itsPrincipal focus. It is typically denoted by letter 'F'.
Plan
To determine the focal length of a concave mirror, byobtainingimageof a distant object.
Apparatus
A concave mirror, a rectangularpiece of woodas a screen or white wall and a meter scale.
Theory
- A distant object situated at a distance which is many many times the focal length of a mirror is regarded as an object at infinity.
- The rays coming from an object at infinity form a set of parallel rays.
- Parallel rays from the object at infinity after suffering reflection at the concave mirror meet in the focal planeof the mirror and form areal invertedanddiminishedimage of the object placed at infinity.
- The distance between the pole of the mirror and the focal plane (The plane which is perpendicular to principal axis and passes through the focal point of the mirror) of the mirror gives the focal length of the mirror.
The mirror formula for a concave mirror is
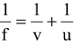
FORMATION OF DIFFERENT TYPES OF IMAGES BY A CONVEX MIRROR IN DIFFERENT POSITIONS OF THE OBJECT:
Formation of Image by a convex mirror
Formation of image depends upon the position of the object. There are six possibilities of the position of object in the case of convex mirror.
- Object at infinity
- Object between infinity and centre of curvature (C)
- Object at centre of curvature (C)
- Object between centre of curvature (C) and Principal focus (F)
- Object at Principal Focus (F)
- Object between Principal Focus (F) and Pole (P)
The type of image formed by a convex mirror primarily depends upon the position of the object in front of the mirror. When an object is moved closer to the mirror, starting from infinity, the following two cases arise:
(i) When the object is at infinity
When the object is at infinity, the rays of light starting from the object on travelling such a large distance are assumed to become parallel to each other while falling on the mirror. These parallel rays of light may fall on the mirror in the following two ways–
- All the incident rays become parallel to the principal axis of the convex mirror.
- All the incident rays falling obliquely to the principal axis.
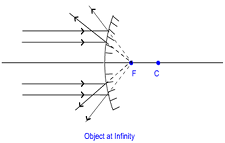
In the above case image is formed at the Focus ‘F’ of the convex mirror, behind the mirror.
Therefore, we can say that when the object is at infinity, the image is formed
- At the Focus ‘F’ behind the mirror.
- Virtual and erect.
- Highly diminished, point sized (much smaller than the object).
(ii) When the object is at finite distance from the convex mirror. i.e. between infinity and the pole P of the convex mirror :
|
When the object is at finite distance i.e. anywhere between infinity and the pole ‘P’ of the convex mirror. The image is formed (a) Between the pole ‘P’ and Focus ‘F’ behind the convex mirror. (b) Virtual and erect. (c) Diminished, smaller than the object. |
|
Image formation by a convex mirror for different positions of the object:
|
Position of the Object |
Position of the image |
Size of the image |
Nature of the image |
|
At infinity |
At the focus F, behind the mirror |
Highly diminished, point-sized |
Virtual and erect |
|
Between infinity and the pole P of the mirror |
Between P and F, behind the mirror |
Diminished |
Virtual and erect |
USES OF CONVEX MIRROR:
Some of the practical uses of convex mirrors are:
- A convex mirror is used as a reflector in street lamps. As a result, light from the lamp diverges over a large area.
- Convex mirrors are used as rear-view mirrors in automobiles (like cars, trucks and buses) to see the objects (traffic) at the rear side.
The convex mirror is preferred as a rear view mirror because:
- A convex mirror always produces an erect image of the objects.
- The size of the image formed by a convex mirror is highly diminished or much smaller than the object, due to which it covers a wide field of view, which enables the driver to view much larger area of the traffic behind him than would be possible with a plane mirror concave mirror.
METHOD TO DISTINGUISH BETWEEN A PLANE MIRROR, A CONCAVE MIRROR AND A CONVEX MIRROR WITHOUT TOUCHING THEM:
To distinguish between a plane mirror, a concave mirror and a convex mirror, without touching them, we simply look at the image of our face in the three mirrors, turn by turn.
All of them will produce an image of our face but of different types.
A plane mirror will produce virtual and erect image of the same size as our face and we will look our normal self.
A concave mirror will produce a virtual, erect and magnified image of our face i.e. our face will look much bigger.
A convex mirror will produce a virtual, erect but diminished image of our face i.e. our face will look much smaller.
|
Mirror type |
Object position |
Image |
|||
|
Plane |
Anywhere* |
Position |
Type |
Orientation |
Size |
|
as for behind the mirror as the object is in front of it |
virtual |
Same as object |
Same as object |
||
|
Concave |
Near mirror* (inside F) |
on the opposite side of the mirror as the object |
virtual |
Same as object |
larger than object (magnified) |
|
exactly at F |
at infinity |
- |
- |
- |
|
|
Object distance less than image distance (outside F) |
On the same side of the mirror as the object |
Real |
Opposite of object |
larger than object (magnified) |
|
|
Object distance is equal to image distance (outside F) |
On the same side of the mirror as the object |
Real |
Opposite of object |
Same as object |
|
|
Object distance is greater than the image distance (outside F) |
On the same side of the mirror as the object |
Real |
Opposite of object |
Smaller than object (diminished) |
|
|
Convex |
Anywhere* |
on the opposite side of the mirror as the object |
virtual |
Same as object |
Smaller than object (diminished) |
SIGN CONVENTION FOR MEASURING DISTANCE IN CONCAVE & CONVEX MIRROR:
- All distances are measured from the pole.
- (The incident ray is taken from left to right.
- Distances measured in the same direction as that of the incident ray are taken to be +ve.
- Distances measured in a direction opposite to the incident ray are taken to be -ve.
- Distances measured upwards and perpendicular to principal axis are taken +ve.
- Distance measured downwards and perpendicular to principal axis are taken -ve.
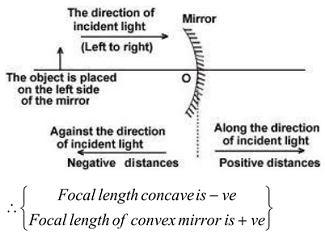
IMPORTANT: These signs are according to the rectilinear co-ordinate system.
NOTE: Always draw a rough ray diagram while solving a numerical problem. Otherwise we will be confuse as to which distance should be taken as +ve & which -ve.
For virtual image : M is +ve [as virtual image is erect ∴ h 1 is + ve as well as h 2 is + ve
For real image : m is -ve [as real image is always inverted ∴ h 2 is – ve while h 1 is + ve]