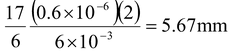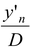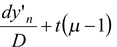Interference: Young’s Double Slit Experiment

Interference: Young’s Double Slit Experiment

It was carried out in 1802 by the English scientist Thomas Young to prove the wave nature of light.

Two slits S 1 and S 2 are made in an opaque screen, parallel and very close to each other. These two are illuminated by another narrow slits S which in turn lit by a bright source. Light wave spread out from S and fall on both S 1 and S 2 which behave like coherent sources. Note that the coherent sources are derived from the same source. In this way, any phase change in S occurs in both S 1 and S 2 . The phase difference (φ 1 - φ 2 ) between S 1 and S 2 is unaffected and remain constant.

Light now spreads out from both S 1 and S 2 falls on a screen. It is essential that the waves from the two sources overlap on the same part of the screen. If one slit is covered up, the other produces a wide smoothly illuminated patch on the screen. But when both slits are open, the patch is seen to be crossed by dark and bright bands called interference fringes.

Condition for bright fringes or maxima

φ = 2nπ  or   path difference ,   p  = nλ   where n = 0, 1, 2, ……

I max = 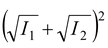(15.30)

Condition for dark fringes or minima

φ = (2n – 1)πorpath difference,  p = (n - 1/2)λ

where n = 1, 2, 3, …………

I min = 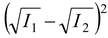(15.31)

The relation between phase difference (φ) and path difference (p) is given by

φ = 2π/λ p (15.32)

How to find the position of the nth maxima or minima on the screen?

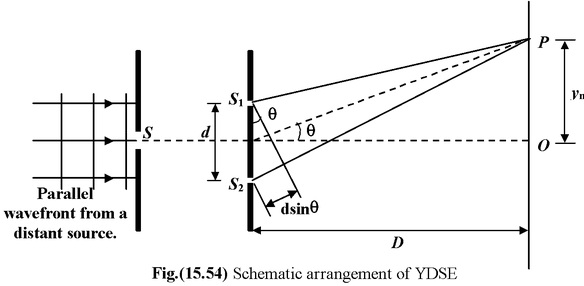
Let P be the position of the nth maxima on the screen. The  two waves arriving at P follow the path S 1 P and S 2 P, thus the path difference between the two waves is

p = S 1 P – S 1 P = d sin θ

From experimental conditions, we know that D >> d, therefore, the angle θ is small,

thus sinθ ≈ tanθ = Yn/D

∴p = d sinθ = d tan θ  = d (Yn/D) ⇒   y n = pD/d

For nth maxima

p = nλ

∴y n =  nλ D/d where  n = 0, 1, 2, ……..(15.33)

For nth minima

p = (n - 1/2)λ

∴y n = (n - 1/2)λD/d where n = 1, 2, 3, ……(15.34)

Note that the nth minima comes before the nth maxima.

Fringe Width

It is defined as the distance between two successive maxima or minima.

∴ω = y n +1 – y n =

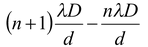
or 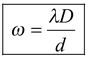(15.35)

Example 15.23

In a YDSE , if D = 2 m; d = 6 mm and λ = 6000 Å, then

(a)find the fringe width

(b)find the position of the 3 rd maxima

(c)find the position of the 2 nd minima

Solution

(a)Using equation (15.33),

ω = λD/d = (6000 x 10 ^-10 )(2)/6 x 10 ^-3 = 0.2 mm

(b)Position of 3 rd maxima is obtained by putting n = 3 in the equation (15.33),

y 3 = 3 λD = 3ω = 3(0.2) = 0.6 mm

(c)Position of 2 nd minima is obtained by putting n = 2 in the equation (15.34),

y 2 = 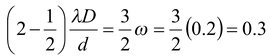mm

Example 15.24

What is the effect on the interference fringes in a YDSE due to each of the following operations.

(a)the screen is moved away from the plane of the slits

(b)the (monochromatic) source is replaced by another (monochromatic) source of shorter wavelength

(c)the separation between the two slits is increased

(d)the monochromatic source is replaced by source of white light

(e)the whole experiment is carried out in a medium of refractive index μ

Solution

(a)Angular separation (= λ/d ) of the fringes remains constant. But the linear separation or fringe width increases in proportion to the distance (D) from the screen.

(b)As λ decreases, fringe width (ω ∝ λ) decreases

(c)As d increases, fringe width (ω ∝ 1/d) decreases

(d)The interference pattern due to different component colours of white light overlap (in-coherently). The central bright fringes of different colours are at the same position. Therefore, the central fringe is white. Since blue colour has the lower λ, the fringe closest on either side of the central white fringe is blue; the farthest is red.

(e)Since in a medium the wavelength of light is λ′ = λ/ μ, therefore the fringe width is given by ω = .

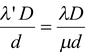Thus, fringe width decreases by μ.

Example  15.25

Light from a source consists of two wavelength λ 1 = 6500Å and λ 2 = 5200Å. If D = 2m and d = 6.5 mm find the minimum value of y (≠ 0) where the maxima of both the wavelengths coincide.

Solution

Let n 1 th maxima of λ 1 coincides with n 2 th maxima of λ 2 .

Then yn1 = yn2

or

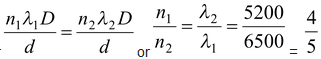
Thus, fourth maxima of λ 1 coincides with fifth maxima of λ 2 .

The minimum value of y (≠ 0) is given by

y = 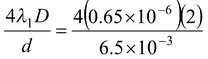= 0.8 mm

Optical Path

It is defined as distance travelled by light in vacuum in the same time in which it travels a given path length in a medium. If light travels a path length d in a medium at speed c, the time taken by it will be (d/c). So optical path length−

L = c o × [d/c] = μd(because  μ = c0/c )(15.36)

Since for all media μ > 1, optical path length is always greater than geometrical path length. When two light waves arrive at a point by travelling different distances in different media, the phase difference between the two is related by their optical path difference instead of simply path difference.

Phase Difference = 2π/ λ (optical path difference) = 2π/ λ L

Fringe Shift

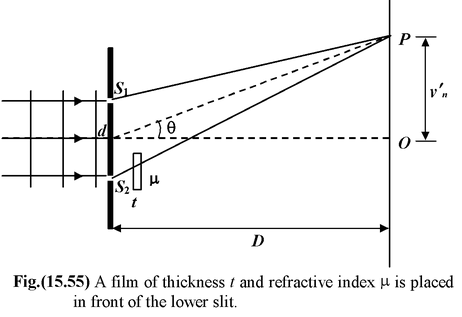
When a transparent film of thickness t and refractive index μ is introduced in front of one of the slits, the fringe pattern shifts in the direction where the film is placed.

or y′ n =

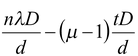
In the absence of film, the position of the nth maxima is given by equation (15.34)

y n = n λD/d

Therefore, the fringe shift is given by

FS = y n - y′ n = (μ - 1) tD/d (15.37)

Note that the shift is in the direction where the film is introduced.

Example 15.26

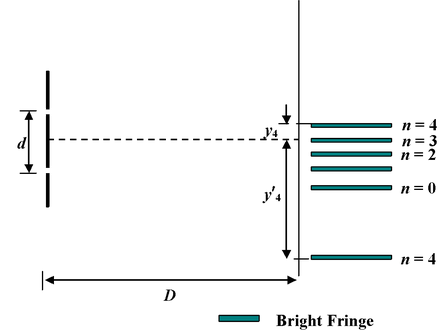
Ιn a YDSE, λ = 6000Å, D = 2 m, d = 6 mm. When a film of refractive index 1.5 is introduced in front of the lower slit, the third maxima shifts to the origin.

(a)Find the thickness of the film

(b)Find the positions of the fourth maxima

Solution

(a)Since 3 rd minima shifts to the origin, therefore, the fringe shift is given by

FS = y 3 = 3 λD/d

From equation (15.37), we know

FS = (μ - 1) tD/d

∴(μ - 1) tD/d = 3 λD/d

or t = 3 λ/μ - 1

Here λ = 0.6 × 10 -6 m;  μ = 1.5

∴t = 3(0.6 x 10 ^-6 )/1.5 -1 = 3.6 μm

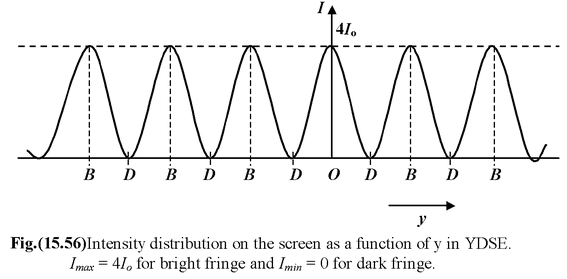
Intensity Distribution

When two coherent light waves of intensity I 1 and I 2 with a constant phase difference φ superimpose, then the resultant intensity is given by

I = I 1 + I 2 + 2 √I 1 I 2 cosφ

In YDSE, usually the intensities I 1 and I 2 are equal

i.e.I 1 = I 2 = I o

Then I = 2I o ( 1+ cos φ)

orI = 4I o cos 2 (φ/2)(15.38)

For maxima:φ = 2nπ ⇒I max = 4I o

For minima:φ = (2n – 1)π⇒I min = 0

Example 15.27

The intensity of the light coming from one of the slits in YDSE is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.

Solution

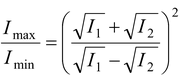
SinceI 1 = 2I o and I 2 = I o ,  therefore

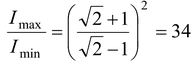
Example 15.28

In a YDSE, λ = 60 nm; D = 2m; λ = 6 mm. Find the positions of a point lying between third maxima and third minima where the intensity is three-fourth of the maximum intensity on the screen.

Solution

Using equation (15.32)

I = 4I o cos 2 φ/2

here I = 3/4 (4I o ) = 3I o

∴cos φ/2 = √3/2

Thus,φ/2 = nπ ± π/6

or φ = 2nπ ± π/3

Since φ =2π/λ p =

∴

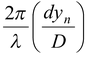
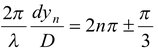
or y n =

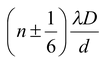
For the point lying between third minima and third maxima,

n = 3 and y 3 =

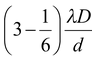
or y 3 = 17/6 λD/d

Putting λ = 0.6 × 10 -6 m;  D = 2m;  d = 6 mm

y 3 =