Resolution of Vectors
Vector of Class 11
If
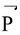 +
+
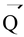 =
=
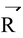 , the resultant, then conversely
, the resultant, then conversely
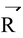 =
=
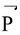 +
+
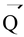 i.e. the vector
i.e. the vector
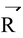 can be split up so that the vector sum of the split parts equals the original vector
can be split up so that the vector sum of the split parts equals the original vector
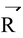 . If the split parts are mutually perpendicular then they are known as components of
. If the split parts are mutually perpendicular then they are known as components of
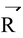 and this process is known as resolution. The orthogonal component of any vector along another direction which is at an angular separation θ is the product of the magnitude of the vector and cosine of the angle between them (θ). Therefore the component of
and this process is known as resolution. The orthogonal component of any vector along another direction which is at an angular separation θ is the product of the magnitude of the vector and cosine of the angle between them (θ). Therefore the component of
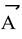 is A cosθ.
is A cosθ.
Note: In physics, resolution gives unique and mutually independent components only if the resolved components are mutually perpendicular to each other. Such a resolution is known as rectangular or orthogonal resolution and the components are called rectangular or orthogonal components.
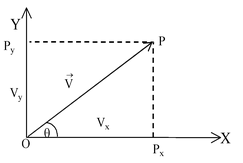
|
|
O – the origin, OP – the given vector
PPx – perpendicular to X axis. PPy – Perpendicular to Y axis.
Vx = V cosθ & Vy = V sinθ |
Unit vector along the direction of
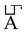 is
is
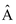 =
=
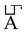 /A, Where A is magnitude of
/A, Where A is magnitude of
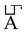 .
.
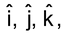 are the unit vectors along positive direction of X, Y and Z axis respectively, then the rectangular resolution of vector
are the unit vectors along positive direction of X, Y and Z axis respectively, then the rectangular resolution of vector
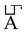 can be represented.
can be represented.
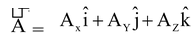 where AX, AY, AZ are the magnitudes of X, Y and Z components of
where AX, AY, AZ are the magnitudes of X, Y and Z components of
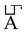 . The magnitude of vector
. The magnitude of vector
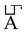 is given by
is given by
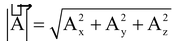 .
.
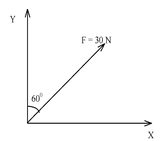
Illustration 8. A force of 30 N is acting at an angle of 600 with the y-axis. Determine the components of the forces along x and y-axes.
|
Solution : Fx = F sin60 0
=
Fy = F cos600 = 30 x1/2 = 15 N |
|
Illustration 9.Four forces act along the sides of a smooth square frame ABCD in the order A → B, B → C, C →D and D → A. If the magnitude of the forces are F1, F2, F3 and F4 respectively, find the resultant force acting on the frame. Assume F 1 = 1 N, F 2 = 2N, F 3 = 3N and F 4 = 4N.
Solution :Let us consider x – y coordinate system. The resultant of all the forces is
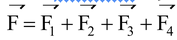 ;
;
After bringing the tails of all the vectors to a point O and substituting
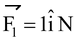 ,
,
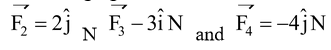
We have,
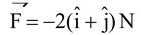
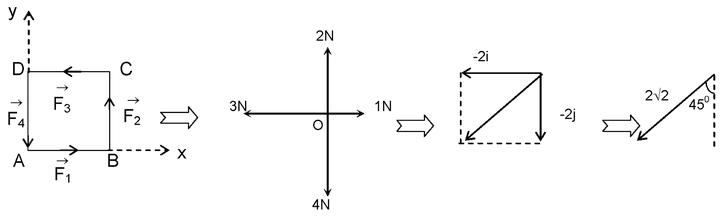 Hence
Hence
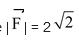 is directed in 3rd quardrant as shown in the figure.
is directed in 3rd quardrant as shown in the figure.

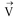
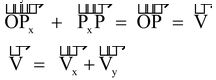
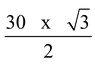 = 15
= 15
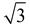 N
N